-
实体对齐(二):BERT-INT
一.摘要
知识图谱对齐旨在链接不同知识图谱中的等效实体。 为了同时利用图结构和额外信息(如名称、描述和属性),大多数工作通过图神经网络链接实体来传播额外信息,尤其是名称。 然而,由于不同知识图谱的异构性,对齐精度将受到聚合不同邻居的影响。 这项工作提出了一个仅利用额外信息的交互模型。 我们不是聚合邻居,而是计算邻居之间的交互,这可以捕获邻居的细粒度匹配。 类似地,属性的交互也被建模。 实验结果表明,在数据集 DBP15K 上,我们的模型在 Hit@1 方面明显优于最先进的方法 1.9-9.7%。
二.背景介绍
DBpedia、Freebase、YAGO 等已作为值得注意的大型且可免费获得的知识图谱 (KG) 发布,可以使许多应用受益,例如问答和推荐。 然而,单个 KG 远不足以支持具有足够事实的此类应用程序,这需要一种有效的方法来使 KG 之间的实体保持一致。 为了解决这个问题,人们非常重视利用图结构来对齐实体。 具体技术已经从传统的 KG 嵌入模型如 MTransE 和 IPTransE发展到最近出现的图神经网络,如基于注意力的 GCN 、highway GCN、关系感知 GCN和 VR-GCN。
尽管在图结构上付出了很多努力,但实体的额外信息(例如名称、描述和属性)可能在 KG 上的许多任务中发挥更重要的作用,因为:(1)KG 通常是稀疏的,具有大量结构嵌入表达能力低的长尾实体, 例如在DBpediaZH中,出现少于5次的长尾实体占74.1%; (2) 现有的工作已经证明了额外信息对几个任务的影响, 例如,HMAN提出,在实体对齐任务上,当忽略实体描述时,HitRatio@1 至少会下降 30%。
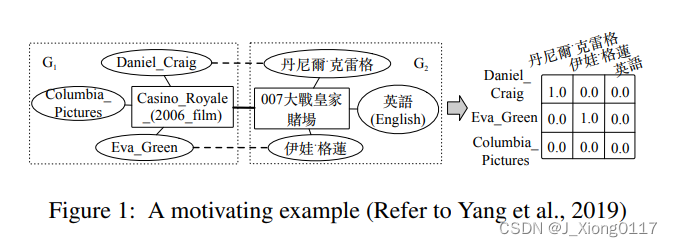
为了利用额外信息对齐 KG,最流行的方法是通过额外信息初始化每个节点的嵌入,并应用变体 GCN 模型通过聚合所有邻居的嵌入来更新节点嵌入。然而,由于不同的 KG 是高度异构的,所以等效实体并不总是共享相似的邻居。 以图 1 中的 HMAN 为例,矩形中的节点是要对齐的实体,椭圆中的节点是邻居。 我们可以看到,对于 G2 中的邻居“English”,无法从 G1 中的邻居中找到对应项,在这种情况下,在 GCN 中传播不同的邻居,尤其是具有 832 关系的邻居“English”等中心实体,可能会引入噪声,从而损害性能。尽管有些工作区分了来自不同邻居的影响,本质上,类 GCN 模型仍然混合所有邻居的额外信息来表示一个实体。HMAN已经意识到了这个问题,因此它彻底分离了额外信息和图结构的建模过程。 但是,它丢弃了邻居的额外信息。 此外,类似于聚合邻居,它将所有属性聚合在一起以表示一个实体,就像大多数工作所做的那样,这也导致了实体之间的噪声匹配。
为了处理由聚合邻居或属性引起的噪声匹配,我们提出了 BERT-INT,即基于 BERT 的交互模型,以统一的方式仅利用额外信息,尤其是当前实体和邻居的名称/描述,以及当前实体的属性。通常,我们模仿人类比较两个实体的认知过程,人类通常首先比较当前实体,然后继续检查是否有相似的邻居。 在此之后,基于任何名称、描述和属性的嵌入,我们比较每对邻居或属性,此后称为交互,而不是聚合它们。 通过这种方式,我们可以捕获邻居之间的细粒度精确/语义匹配,并消除来自不同邻居的负面影响,如图 1 右侧所示。
尽管我们利用了邻居的额外信息,但与变体 GCN 模型不同,我们的模型完全忽略了 KG 的结构特征,因为我们从不在图中传播邻居的信息。从这个角度来看,我们声称 BERT-INT 只利用了额外信息。 正因为如此,BERT-INT 能够进行归纳学习,即我们可以在两个对齐的 KG 上训练 BERT-INT,并将其应用于预测其他 KG 中未见实体之间的匹配。 但是,如果采用变体 GCN 模型,则测试实体应包含在训练 KG 中。总之,我们提出了一种基于归纳学习的模型,以综合利用名称/描述-视图交互、邻居-视图交互和属性-视图交互来对齐实体。 通过实验,我们证明 BERT-INT 在 HitRatio@1 中的性能明显优于最先进的模型 1.9-9.7%。
三.BERT-INT
1.问题定义
知识图谱(Knowledge Graph):定义 G = ( E , R , A , V ) G = (E,R,A,V) G=(E,R,A,V)为一个知识图谱(KG),其中 e ∈ E , r ∈ R , a ∈ A , v ∈ V e \in E,r \in R, a \in A,v \in V e∈E,r∈R,a∈A,v∈V分别表示实体,关系,属性及其对应属性值。 N τ ( e ) = { ( r i , e i ) } i = 1 ∣ N τ ( e ) ∣ N^{\tau}(e) = \{(r_i,e_i)\}^{|N^{\tau}(e)|}_{i=1} Nτ(e)={(ri,ei)}i=1∣Nτ(e)∣表示实体 e 的所有 τ跳邻居的集合,τ 为跳数,其中第 i 个邻居都包含一个邻居关系 r i r_i ri 和对应的实体 e i e_i ei。 A ( e ) = { ( a i , v i ) } i = 1 ∣ A ( e ) ∣ A(e) = \{(a_i,v_i)\}^{|A(e)|}_{i=1} A(e)={(ai,vi)}i=1∣A(e)∣表示 e 的属性集,其中第 i 个属性中的每一个都包含一个名称 ai 和对应的值 vi。 N ( e ) N(e) N(e)没有 τ 表示 e 的所有邻居。 ∣ N τ ( e ) ∣ |N^{\tau}(e)| ∣Nτ(e)∣和 ∣ A ( e ) ∣ |A(e)| ∣A(e)∣分别表示 N τ ( e ) N^{\tau}(e) Nτ(e)和 A ( e ) A(e) A(e)的数量。
知识图谱对齐(Knowledge Graph Alignment):
给定两个知识图谱 G 和 G′ 以及一组已经对齐的实体对 I = {(e ~ e ′ )},我们旨在学习一个排序函数 f : E × E′ → R 来计算两个实体之间的相似度分数, 在此基础上,我们将在 E’ 中正确对齐的所有实体e’尽可能高地排列到任何查询的实体 e。2.BERT-INT模型
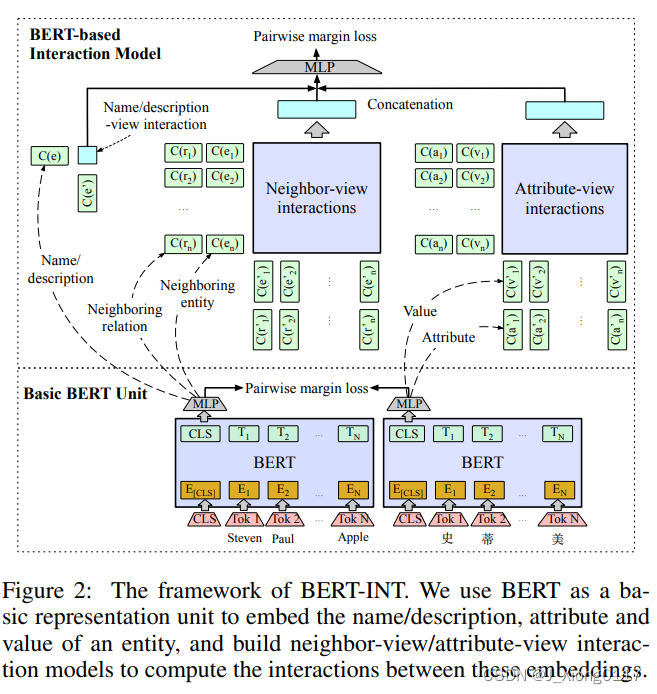
本节介绍所提出的 BERT-INT,它由一个 BERT 模型组成,该模型用作嵌入实体的名称、描述、属性和值的基本表示单元,以及一个基于BERT的这些嵌入之间来计算交互的交互模型,其中交互进一步划分为名称/描述视角交互、邻居视角交互和属性视角交互。应用统一的双重聚合函数从邻居视角和属性视角交互中提取特征,以评估实体间的匹配分数。此外,为了构建全面的邻居视角交互,还考虑了相邻实体之间的交互、相应的相邻关系和多跳邻居(图 2 显示了整个框架)。
2.1 基础BERT单元
我们将实体对齐视为下游目标,以微调预训练的 BERT 模型。 具体来说,我们首先构造训练数据 D = {(e, e′+, e′−)},其中每个三元组 (e, e′+, e′−) ∈ D 包含一个查询实体e ∈ E,正确对齐的对应物 e’+ ∈ E’ 和从 E’ 随机采样的负对应物 e’−。 对于数据集中的每个实体 e,我们应用一个预训练的多语言 BERT 来接受其名称/描述作为输入,通过 MLP 层过滤 BERT 的 CLS 嵌入以获得。
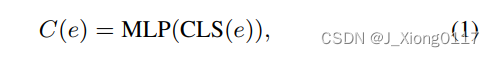
并使用成对的边际损失来微调 BERT:
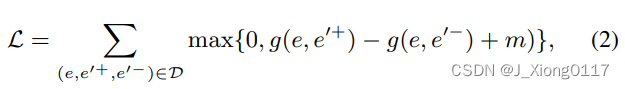
其中 m 是正对和负对之间的边距,g(e, e’) 被实例化为 l1 距离以测量 C(e) 和 C(e’) 之间的相似性。 负对根据两个实体的余弦相似度进行采样。
对于BERT的输入,我们优先考虑描述,因为它包含更丰富的信息。 我们在缺少描述时使用名称。 与直接使用描述的嵌入来对齐实体的 HMAN 不同,我们使用这些嵌入作为基本单元来组成以下交互模型。 请注意,我们还可以将基本 BERT 单元与以下交互模型连接为端到端模型,以同时微调 BERT 并训练交互模型。 在实践中,考虑到 GPU 内存和运行效率,我们预先微调了基本的 BERT 单元,并将其参数冻结在下面的交互模型中。2.2 基于BERT的交互模型
在基本 BERT 单元的基础上,我们构建了由名称/描述-视图交互、邻居-视图和属性-视图交互组成的交互模型。
名称/描述视图交互
我们将基本的 BERT 单元应用于 e 和 e’ 的名称/描述以获得 C(e) 和 C(e’),然后计算它们的余弦相似度作为名称/描述-视图交互。
邻视图交互
我们建立了邻居 N (e) 和 N (e’) 之间的相互作用。 总体思路是比较每个邻居对的名称/描述,而不是像现有工作那样通过聚合所有邻居的名称/描述来学习 e 或 e’ 的全局表示。这种类似的想法被广泛用于信息检索,以捕获查询和候选文档之间的精确匹配和软匹配。 具体来说,我们应用基本 BERT 单元来获得 { C ( e i ) } i = 1 ∣ N ( e ) ∣ \{C(e_i)\}^{|N(e)|}_{i=1} {C(ei)}i=1∣N(e)∣和 { C ( e i ′ ) } i = 1 ∣ N ( e ′ ) ∣ \{C(e'_i)\}^{|N(e')|}_{i=1} {C(ei′)}i=1∣N(e′)∣ 对于 e 和 e′ 相邻实体基于它们的名称/描述,计算两个嵌入集之间的相似度矩阵,然后应用对偶聚合函数从矩阵中提取相似度特征。我们用 S 表示 e 和 e’ 的邻居之间的交互,每个元素 s i j s_{ij} sij 代表相互作用,即余弦相似度 s i j = C ( e i ) ⋅ C ( e j ′ ) ∥ C ( e i ) ∥ ⋅ ∥ C ( e ′ j ) ∥ s_{ij} = \frac {C(e_i)·C(e'_j)}{∥C(e_i)∥· ∥C(e′_j)∥} sij=∥C(ei)∥⋅∥C(e′j)∥C(ei)⋅C(ej′)在 C ( e i ) C(e_i) C(ei) 和 C ( e ′ j ) C(e′_j) C(e′j) 之间,其中 C ( e i ) C(e_i) C(ei) 和 C ( e ′ j ) C(e′_j) C(e′j) 由 公式(1) 获得,对于 e 的第 i 个邻居和 对应的 e’ 的第 j 个邻居。
我们应用双重聚合函数来提取沿 S 的行和列的相似性特征。CNN 和 RNN 通常用作聚合函数,从两个句子之间的相似性矩阵中提取匹配模式。 与句子不同,邻居是无序的,彼此独立的。 因此,我们采用 RBF 核聚合函数来提取关于相似性累积的特征。
在使用 RBF 内核聚合之前,我们首先对每一行 S i = s i 0 , ⋅ ⋅ ⋅ ⋅ , s i j , ⋅ ⋅ ⋅ , s i n S_i = {s_{i0}, ····, s_{ij},···, s_{in}} Si=si0,⋅⋅⋅⋅,sij,⋅⋅⋅,sin 应用最大池化操作以获得最大相似度 s i m a x s^{max}_i simax, 即我们选择对于e的第i个邻居,最有可能与 e’ 的邻居对齐的对应物。 这是因为,遵循一对一映射假设,我们只关心最可能对齐的对应物与e的给定邻居的相似程度。换句话说,不要求 e 的邻居与 e’ 的所有邻居相似,因此除了最大的相似性之外的其他相似性被丢弃。 接下来,将最大值 s i m a x s^{max}_i simax 转换为基于行的特征向量 K r ( S i ) K^r (S_i) Kr(Si),其中第 l 个元素 K l ( s i m a x ) K_l(s^{max}_i) Kl(simax) 中的每一个都由第 l 个 RBF 内核转换为均值 µ l µ_l µl 和方差 σ l σ_l σl。 然后将所有行的 K r ( S i ) K^r(S_i) Kr(Si) 平均为基于行的相似性嵌入 φ r ( N ( e ) , N ( e ′ ) ) φ^r(N (e), N (e′)) φr(N(e),N(e′)):
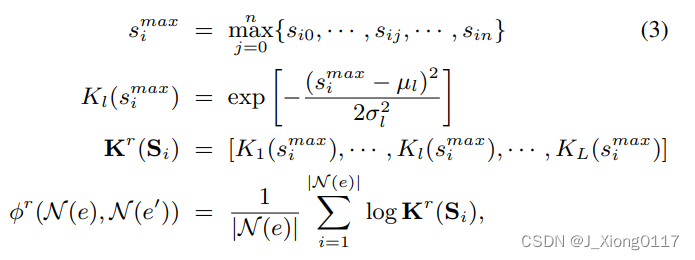
其中 n 是所有实体的最大邻居数。 如果实数 |N (e)| 小于 n,则S将被填充为零。 核用于将一维相似度转换为L维相似度以增强区分能力,其中μ=1和σ→0的核只考虑邻居之间的精确匹配,其他的则捕获邻居之间的语义匹配。
上述过程沿行聚合特征,这反映了每个邻居 e i ∈ N ( e ) e_i \in N (e) ei∈N(e) 与 e’ 的邻居 N ( e ′ ) N (e') N(e′) 的相似程度。 类似地,我们还沿着列聚合特征来捕捉每个邻居 e ′ j ∈ N ( e ′ ) e′_j \in N (e′) e′j∈N(e′) 与 e 的邻居 N ( e ) N (e) N(e) 的相似程度。 最后,将行聚合向量 ϕ r ϕ^r ϕr 和列聚合向量 ϕ c ϕ^c ϕc 连接起来作为最终的相似性嵌入:
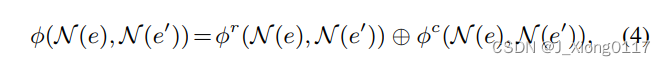
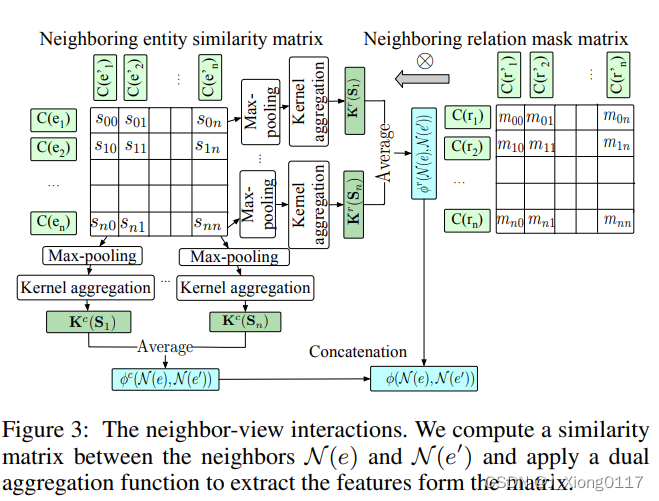
其中⊕表示串联操作, 图 3 说明了邻居视图交互。
相邻关系掩码矩阵
如果对应关系也相似,一对邻居更有说服力支持两个实体的对齐。 换句话说,对于 e 的三元组 ( e , r i , e i ) (e, r_i, e_i) (e,ri,ei) 和 e’ 的三元组 ( e ′ , r j ′ , e j ′ ) (e', r'_j, e'_j) (e′,rj′,ej′),如果 e i e_i ei 与 e j ′ e'_j ej′ 非常相似并且 r i r_i ri 也类似于 r j ′ r'_j rj′,两个实体 e 和 e’ 将更有可能对齐。 根据这个假设,我们不仅计算了相邻实体之间的相似度矩阵 S,还计算了相应的相邻关系之间的相似度矩阵 M。M 被视为掩码矩阵并与 S 相乘,即 S i j = S i j ⊗ M i j S_{ij} = S_{ij} ⊗ M_{ij} Sij=Sij⊗Mij ,其中 ⊗ 表示元素乘积。 为了计算 M,我们需要嵌入每个相邻关系。 一种流行的方法是通过关联的头尾实体对近似地表示一个关系,假设两个关系与更相似的头尾对相关联,则它们更相似。 具体来说,我们对所有关联的头部实体的 C(e) 进行平均,并对所有尾部实体的 C(e) 进行平均,并将它们连接起来以表示关系。
多跳邻居之间的交互
直观地说,单跳邻居在对齐两个实体中起着最重要的作用。 然而,多跳邻居在某些情况下也会影响对齐结果,因为由于两个 KG 的异质性, G 中一个实体的直接邻居可能会显示为 G’ 中对应实体的远邻居。因此,我们还考虑了多跳邻居之间的交互。 具体来说,给定一跳邻居 N 1 ( e ) N^1(e) N1(e)和 N 1 ( e ′ ) N^1(e') N1(e′) 以及多跳邻居 N m ( e ) N^m(e) Nm(e)和 N m ( e ′ ) N^m(e') Nm(e′),我们构建了 N 1 ( e ) N^1(e) N1(e)和 N 1 ( e ′ ) N^1(e') N1(e′), N 1 ( e ) N^1(e) N1(e)和 N m ( e ′ ) N^m(e') Nm(e′), N m ( e ) N^m(e) Nm(e)和 N 1 ( e ′ ) N^1(e') N1(e′), N m ( e ) N^m(e) Nm(e)和 N m ( e ′ ) N^m(e') Nm(e′)之间的交互矩阵,使用和等式(3)和等式(4)相同的聚合函数分别提取相似度向量,并将它们连接起来作为最终的邻居相似度嵌入。
属性视图交互
我们还建立了属性 A(e) 和 A(e’) 之间的交互。 与唯一的名称或描述不同,属性是一组属性-值对,类似于相邻的关系-实体对。 因此,与邻居视图交互类似,我们还比较每个属性对,而不是像现有工作那样通过聚合所有属性来学习 e 或 e’ 的全局表示。具体来说,在图 3 中,我们将相邻实体之间的相似度矩阵更改为嵌入 e 值的嵌入 C ( v i ) i = 1 ∣ A ( e ) ∣ {C(v_i)}^{|A(e)|}_{i=1} C(vi)i=1∣A(e)∣之间的相似度矩阵和的 e’ 值的嵌入 C ( v ′ i ) i = 1 ∣ A ( e ′ ) ∣ {C(v′_i)}^{|A(e′)|}_{i=1} C(v′i)i=1∣A(e′)∣ ,并将相邻关系之间的掩码矩阵更改为嵌入之间的掩码矩阵 e 属性的嵌入 C ( a i ) i = 1 ∣ A ( e ) ∣ {C (a_i)}^{|A(e)|}_{i=1} C(ai)i=1∣A(e)∣ 和e’ 的属性嵌入 C ( a ′ i ) i = 1 ∣ A ( e ′ ) ∣ {C(a′_i)}^{|A(e′)|}_{i=1} C(a′i)i=1∣A(e′)∣ 个。 假设如果对应的属性也相似,则一对值对于支持两个实体的对齐更有说服力。 然后我们使用与等式(3)和等式(4)相同的聚合函数来生成属性相似度向量 ϕ(A(e), A(e′))。 请注意,我们忽略了邻居的属性,因为一方面,合并邻居的属性会导致嵌套交互,这是低效的。 另一方面,对于对齐 e 和 e’,它们自身的属性是最重要的。
最后组合
给定两个实体的描述/名称之间的余弦相似度 cos(C(e), C(e′)),邻居相似度向量 φ(N(e), N(e′)) 和属性相似度向量 φ( A(e), A(e’)),我们将它们连接在一起并应用 MLP 层来获得 e 和 e’ 之间的最终相似度得分:
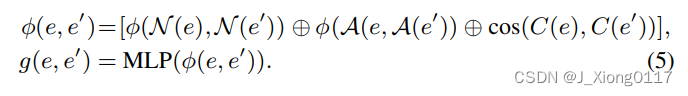
最后,将 g(e, e’) 注入与等式(2)相同的成对损失函数中,以优化 MLP 的参数。 请注意,BERT 的参数已在第 3.1 节中由基本 BERT 单元进行了微调,并在此阶段被冻结。
2.3 实体对齐
给定 G 中的实体 e,我们首先快速过滤 G’ 中的 top-κ 候选,然后从候选中准确推断出对应物。 具体来说,我们应用基本 BERT 单元通过 公式(1) 获得每个实体的嵌入,计算来自 G 的 e 的嵌入与来自 G’ 的每个实体的嵌入之间的余弦相似度,并返回 top-κ 相似度 作为 e 的候选者的实体。 然后对于 e 和每个候选者,我们应用基于 BERT 的交互模型来推断它们之间的匹配分数,并对所有候选者进行排名以进行评估。 候选选择过程可以通过交互模型显着提高对齐效率。
2.4 效果
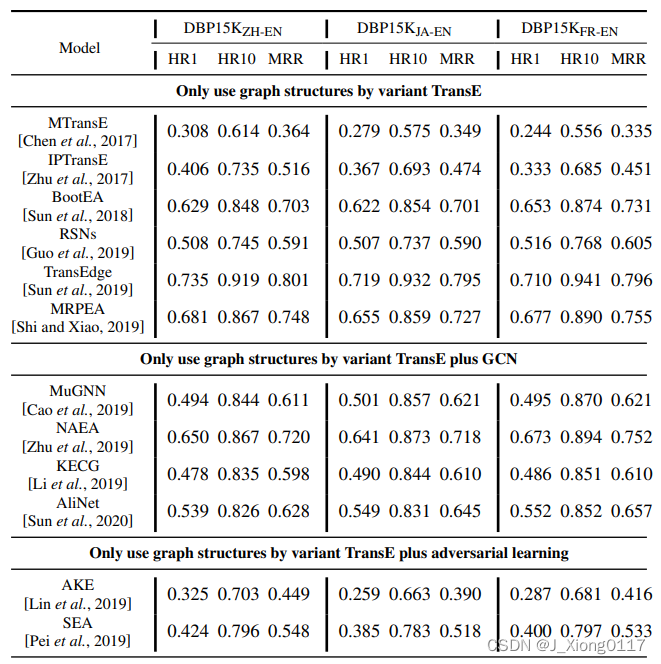
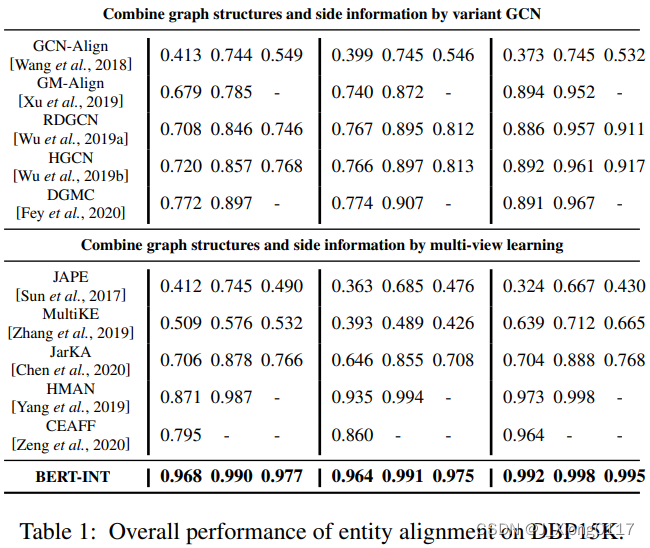
四.总结
本文通过基于 BERT 嵌入构建邻居或属性之间的交互来解决知识图对齐问题,可以获得邻居或属性的细粒度匹配。 所提出的模型可以在所有最先进的模型中实现最佳性能,并且与其他模型相比可以进行归纳学习。
五.附录
论文链接:https://www.ijcai.org/Proceedings/2020/0439.pdf
代码链接:https://github.com/kosugi11037/bert-int -
相关阅读:
C++11 shared_ptr unique_ptr weak_ptr
【JavaEE初阶】 volatile关键字 与 wait()方法和notify()方法详解
微信小程序开发基础(03视图与逻辑)
一文带你摸清设计模式之单例模式!
二叉树前序、中序、后序遍历
【BOOST C++ 5 】通信(03 网络编程 )
无源无线测温系统设计及在高压开关柜中的应用
Stable-diffusion WebUI API调用方法
攻击方法与工业控制系统安全
基于php的就业咨询网站
- 原文地址:https://blog.csdn.net/u013010473/article/details/127753910