常见算法排序总结

常见算法排序

1.冒泡排序

将后一位数字与前一位数字对比，小的数字放前面，大的数字放后面，依次往后，直到最后一位，这样大的数字就会跑到最后面。一共这样交换n轮，每一轮去掉最后n个已经冒泡好的数字。

复杂度分析：

时间复杂度O(n²)，空间复杂度O(1)，结构稳定性好。

代码：

def swap(arr, index1, index2):
    temp = arr[index1]
    arr[index1] = arr[index2]
    arr[index2] = temp

def bubbleSort(arr):
    length = len(arr)
    for j in range(length-1):
        for i in range(length-1-j):
            if arr[i] > arr[i+1]:
                swap(arr, i+1, i)
    print(arr)

arr = [5, 8, 6, 3, 9, 2, 1, 7]
bubbleSort(arr)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2.选择排序

第一轮，将数组中的最小值与第一位数字交换，第二轮，将数组中除去第一位数字，剩下的数字找到最小值与第二位数字交换，依次类推，最小的数字都会跑到前面来，这样就排好序啦

复杂度分析：

时间复杂度O(n²)，空间复杂度O(1)，结构稳定性差。

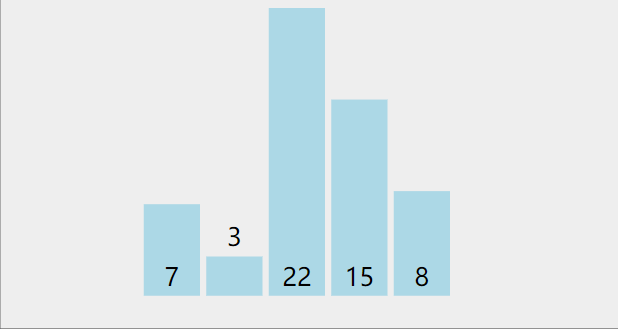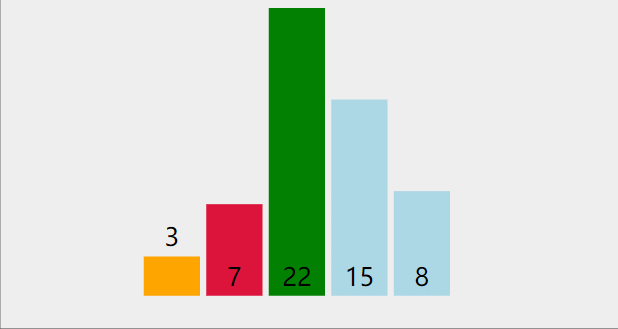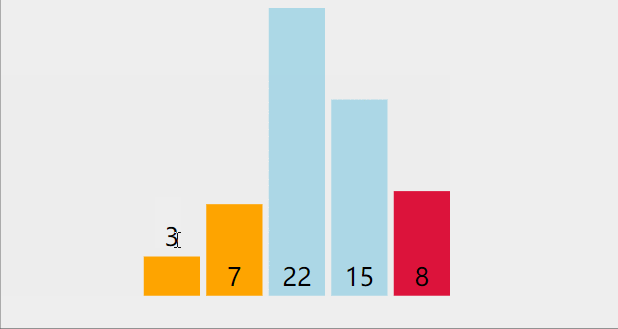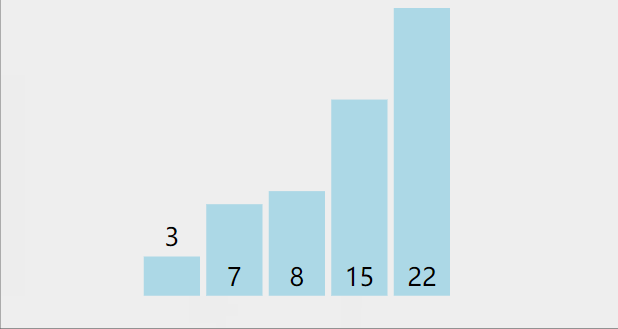
代码：

def swap(arr, index1, index2):
    temp = arr[index1]
    arr[index1] = arr[index2]
    arr[index2] = temp


def selectionSort(arr):
    length = len(arr)
    if not arr or length <= 1:
        print(arr)

    for i in range(length):
        min_index = i
        for j in range(i, length):
            if arr[j] < arr[min_index]:
                min_index = j
        temp = arr[i]
        arr[i] = arr[min_index]
        arr[min_index] = temp
        print(arr)

arr = [7, 3, 22, 15, 18]
selectionSort(arr)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3.插入排序

第一轮，第二位数字与前面的数字对比，比前面的数字小就一直往前插入，第二轮，第三位数字与前面的数字对比，比前面的数字小就一直往前插入，以此类推

复杂度分析：

时间复杂度O(n²)，空间复杂度O(1)，结构稳定性好。

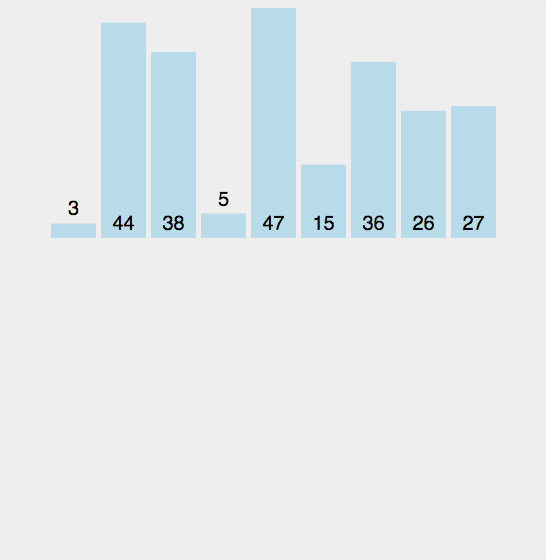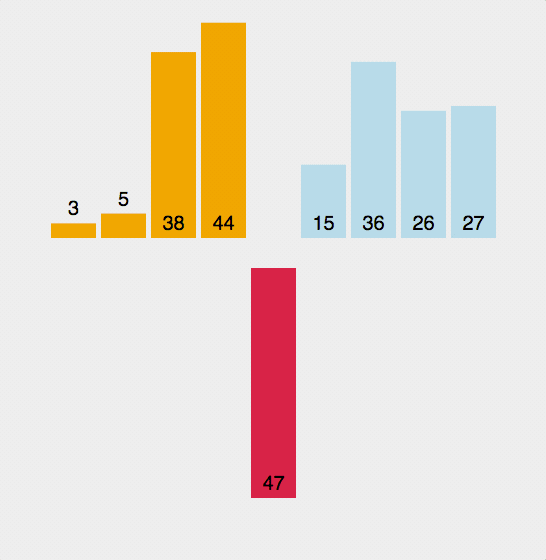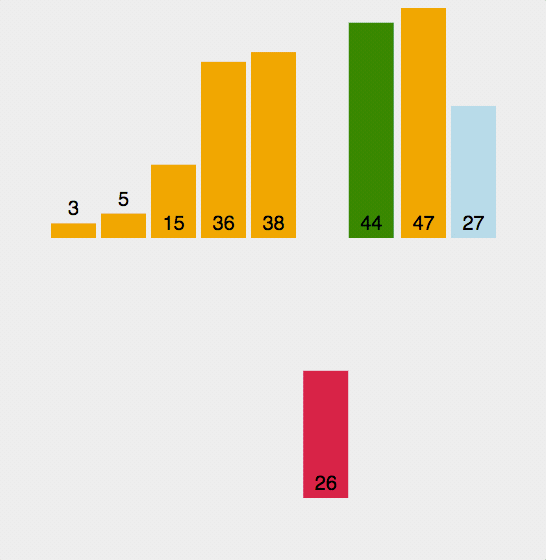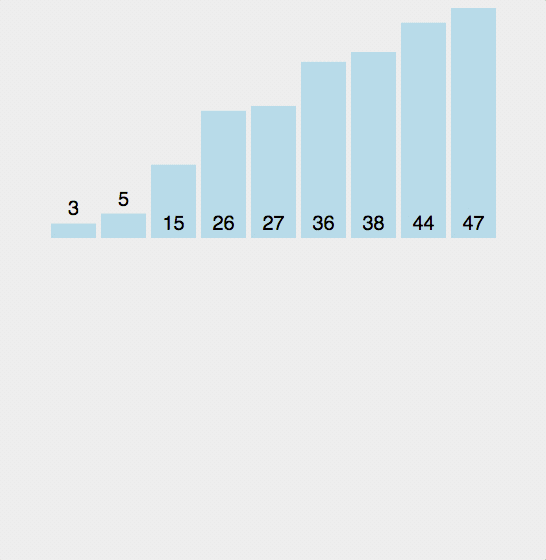
代码：

def swap(arr, index1, index2):
    temp = arr[index1]
    arr[index1] = arr[index2]
    arr[index2] = temp

def insertSort(arr):
    length = len(arr)
    if not arr or length <= 1: # 数组为空或者长度为1时直接返回
        print(arr)
    
    for i in range(1,length):
        while i:
            if arr[i] < arr[i-1]:
                swap(arr, i, i-1)
            else:
                break
            i -= 1
    print(arr)

arr = [3, 44, 38, 5, 47, 15, 36, 26, 27]
insertSort(arr)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

4.归并排序

归并排序有点向二分法，递归到最小范围，比较左边的右边的数字

复杂度分析：

时间复杂度O(NlogN)，空间复杂度O(N)，结构稳定性好。

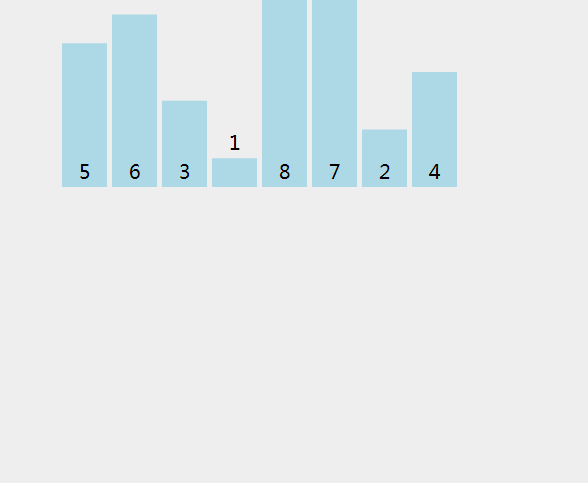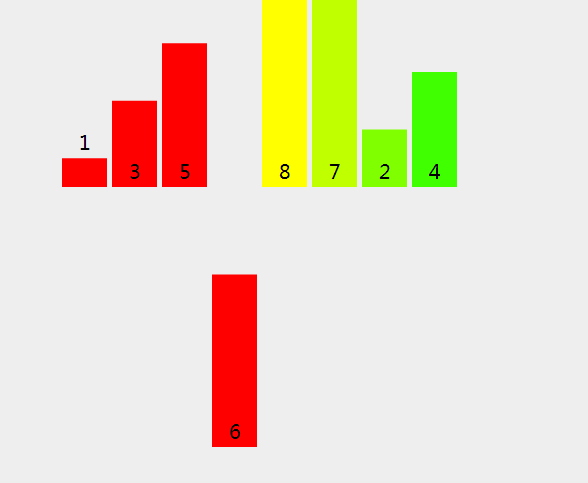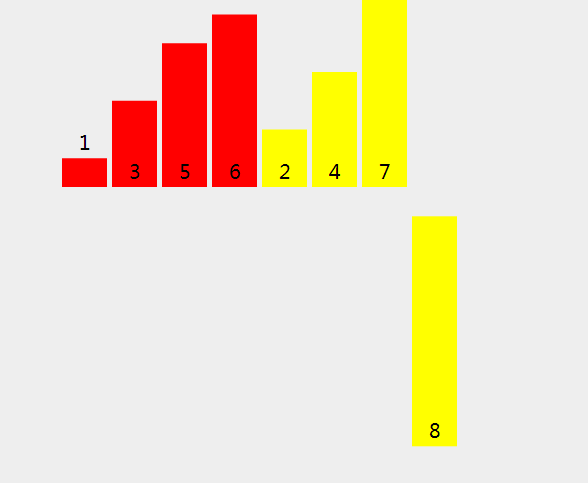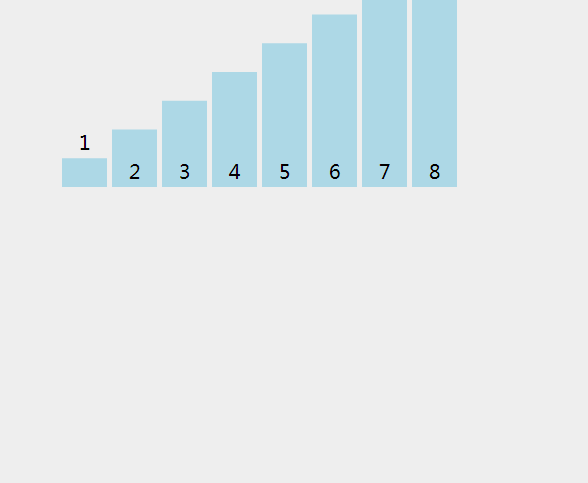
这个动图更加形象

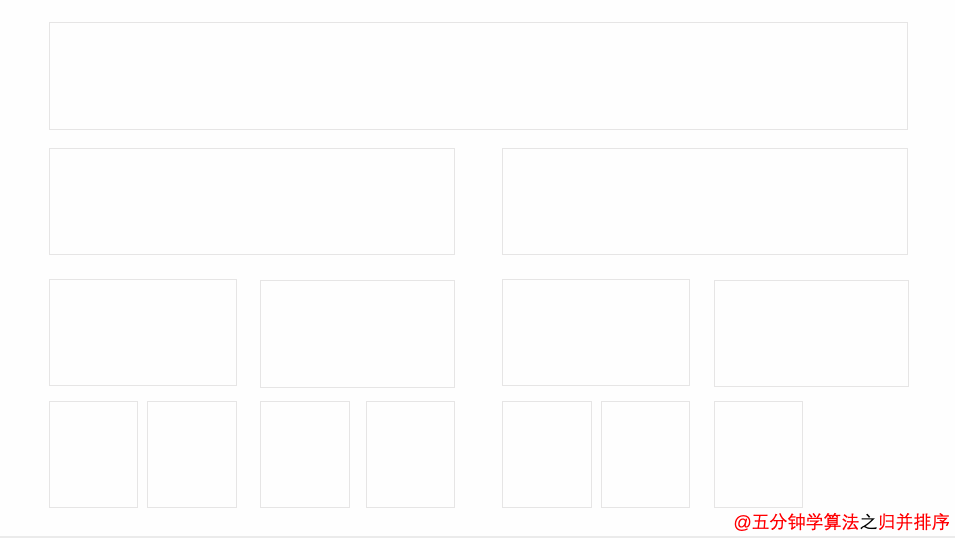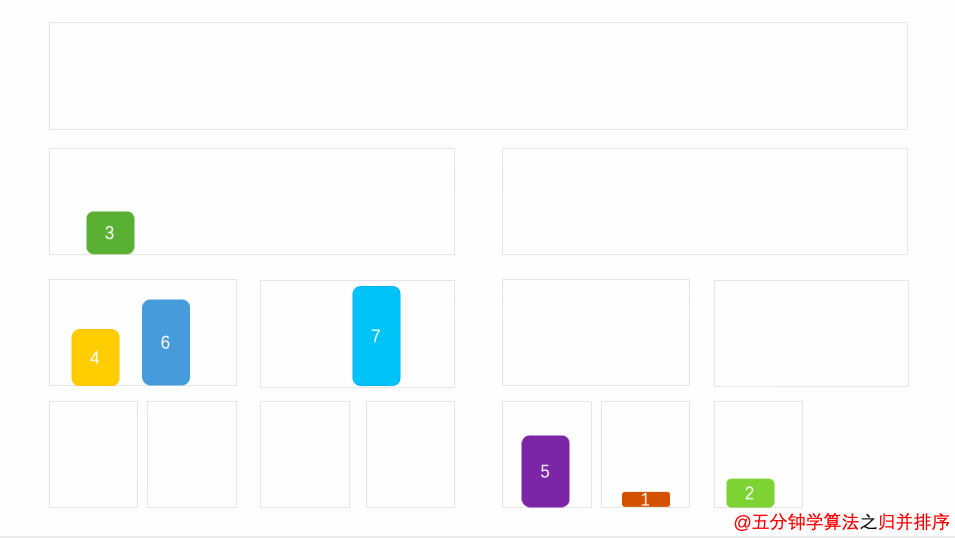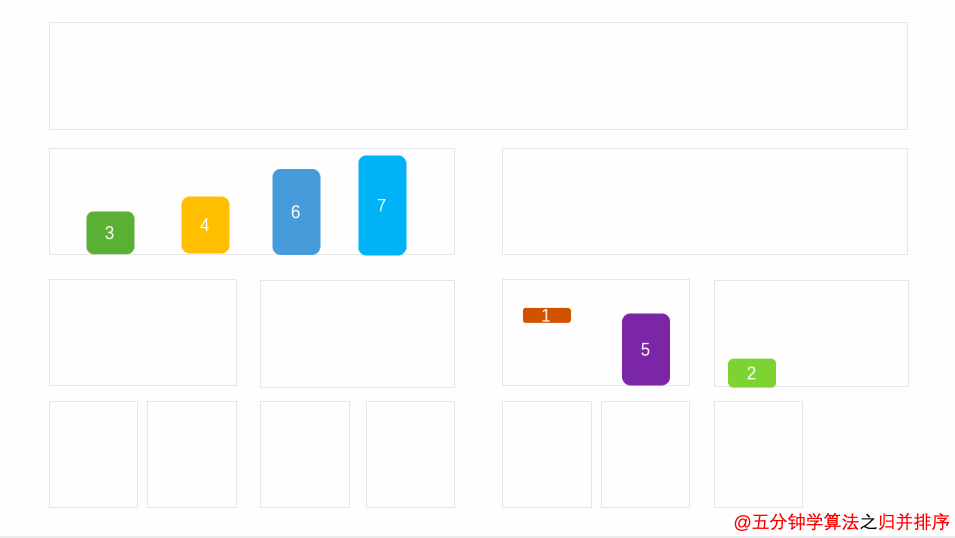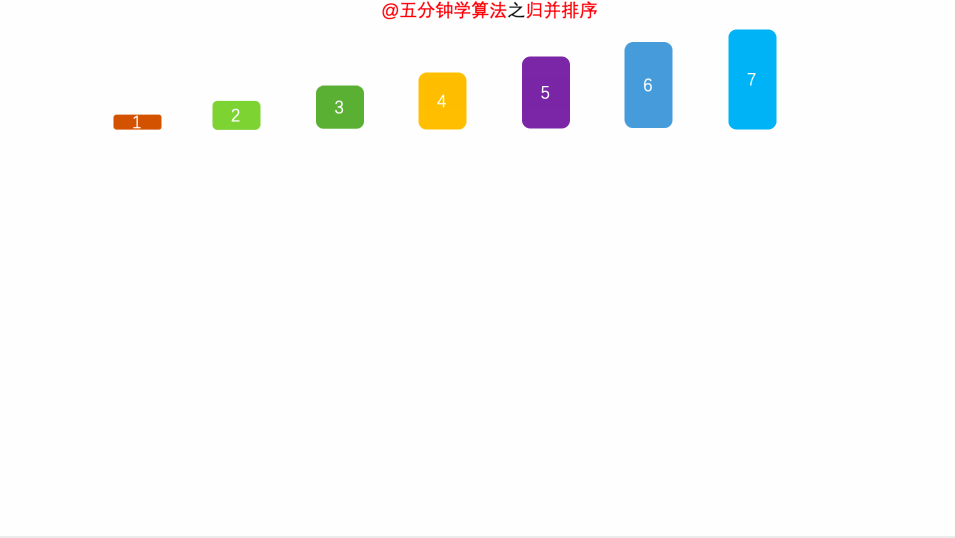
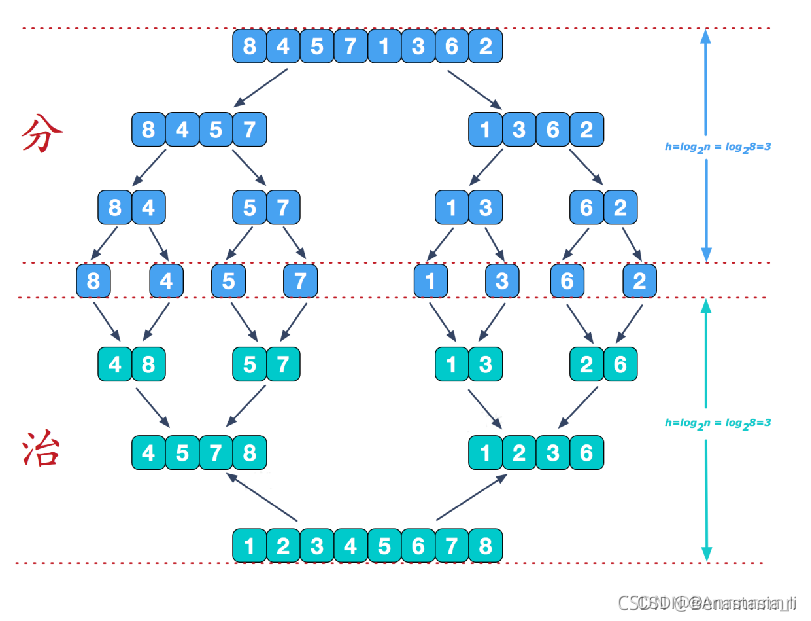
代码：

new_arr = [0 for i in range(8)] # 暂存数组
arr = [5, 6, 3, 1, 8, 7, 2, 4] # 原数组
L = 0
R = len(arr)-1

def merge(arr, L, M, R):
    left = L # 左边的指针
    right = M + 1 # 右边的指针
    k = L # 储存新数组的指针

    while left <= M and right <= R: # 左边和右边对比，小的数值存入新数组
        if arr[left] < arr[right]:
            new_arr[k] = arr[left]
            left += 1
        else:
            new_arr[k] = arr[right]
            right += 1
        k += 1

    while left <= M: # 剩余左边的数字存入数组
        new_arr[k] = arr[left]
        left += 1
        k += 1

    while right <= R: # 剩余右边的数字存入数组
        new_arr[k] = arr[right]
        right += 1
        k += 1
    # 移动回原数组
    for i in range(L,R+1):
        arr[i] = new_arr[i]
    return arr

def mergeSort(arr, L, R):

    if L >= R:
        return
    M = L + ((R - L)>>1)
    mergeSort(arr, L, M)
    mergeSort(arr, M+1, R)

    arr = merge(arr, L, M, R)
    return arr

result = mergeSort(arr, L, R)
print(result)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

5.快排

随机生成一个锚点，大于锚点的放左边，小于锚点的放右边，往下递归时，把锚点的位置代入到起始位置

复杂度分析：

时间复杂度O(NlogN)，空间复杂度O(logN)，结构稳定性差。

代码：

import random

def swap(arr, t, R):
    temp = arr[t]
    arr[t] = arr[R]
    arr[R] = temp

def partition(arr, l, r):
    x = random.randint(l, r)
    v = arr[x]
    print(v)
    swap(arr, x, r)
    low = l
    high = r
    p = l
    while low < high:
        while low < high and arr[low] < v:
            low += 1
        arr[high] = arr[low]
        while low < high and arr[high] >= v:
            high -= 1
        arr[low] = arr[high]
    arr[high] = v
    return high

def quickSort(arr, L, R):
    if L>=R:
        return
    p = partition(arr, L, R)
    quickSort(arr, L, p-1)
    quickSort(arr, p+1, R)
    return arr

arr = [3, 6, 2, 4, 9, 6, 6, 6]
# arr = [22, 33, 49, 47, 33, 12, 68, 29]
length = len(arr)
quickSort(arr, 0, length-1)
print(arr)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

6.堆排序

复杂度分析：

时间复杂度O(NlogN)，空间复杂度O(1)，结构稳定性差。
代码：

def swap(arr, index1, index2):
    temp = arr[index1]
    arr[index1] = arr[index2]
    arr[index2] = temp

def heapInsert(arr, length):
    for index in range(length):
        while index > 0 and arr[index] > arr[(index-1)//2]: # 父比子大，交换位置
            swap(arr, index, (index-1)//2)
            index = (index-1)//2
#
# def heapify(arr, index, heapSize):
#     while index * 2 + 1 < heapSize:
#         left = index*2+1
#         if left+1 < heapSize and arr[left+1] > arr[left]: # 左孩子和右孩子比较
#             swap(arr, left+1, index) # 右孩子大，右孩子和父交换位置
#             index = left+1
#         elif arr[left] > arr[index]: # 左孩子和父比较
#             swap(arr, left, index) # 左孩子比父大，交换位置
#             index = left
#         else:
#             break

def heapSort(arr):
    heapSize = len(arr)
    if not arr or heapSize<2:
        return arr
    while heapSize:
        heapInsert(arr, heapSize)
        swap(arr, 0, heapSize - 1)
        heapSize -= 1
    print(arr)

arr = [1, 6, 4, 8, 6, 7]
heapSort(arr)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

7.桶排序

按照十进制，准备10个桶，分别对应0-9，现将个位数相同的放在一个桶里，先进桶的先出桶，形成一个新数组。然后对比十位上的数，分别放到对应的桶里形成新数组，以此类推，最后形成新的数组

def bucketSort(arr):
    digit = getDigit(max(arr))
    length = len(arr)
    bucket = [0 for i in range(length)]

    for d in range(digit):
        count = [0 for i in range(10)]
        for each in arr:
            r = getRemainder(each, d)
            count[r] = count[r] + 1
        for i in range(1,10):
            count[i] = count[i] + count[i-1]
        for i in range(length):
            each = arr[length-1-i]
            r = getRemainder(each, d)
            bucket[count[r]-1] = each
            count[r] -= 1
        for i in range(length):
            arr[i] = bucket[i]
    print(arr)
    # print(arr)

# arr = [23, 100, 24, 34, 65, 77, 78, 99, 145, 56, 178]
arr = [100, 23, 34, 24, 145, 65, 56, 77, 178, 78, 98, 99]
bucketSort(arr)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

尽量用快拍，快排一般情况下是最快的，实在不行用堆排，需要用到稳定性的时候用归并

1.基于比较的排序不能找到时间复杂度在O(NlogN)以下
2.还没有找到时间复杂度在O(NlogN)以下，空间复杂度在O(N)以下，且稳定的排序