【LeetCode】No.88. Merge Sorted Array -- Java Version

题目链接：https://leetcode.com/problems/merge-sorted-array/

1. 题目介绍（Merge Sorted Array）

You are given two integer arrays nums1 and nums2, sorted in non-decreasing order, and two integers m and n, representing the number of elements in nums1 and nums2 respectively.

【Translate】：给定两个整数数组nums1和nums2，它们按非递减顺序排序（递增），以及两个整数m和n，分别表示nums1和nums2中的元素数量。

Merge nums1 and nums2 into a single array sorted in non-decreasing order.

【Translate】： 将nums1和nums2合并到一个以非递减顺序排序的数组中。

The final sorted array should not be returned by the function, but instead be stored inside the array nums1. To accommodate this, nums1 has a length of m + n, where the first m elements denote the elements that should be merged, and the last n elements are set to 0 and should be ignored. nums2 has a length of n.

【Translate】：最终排序的数组不应该由函数返回，而是存储在数组nums1中。为了适应这一点，nums1的长度为m + n，其中前m个元素表示应该合并的元素，最后n个元素设置为0，可以被忽略。Nums2的长度是n。

【测试用例】：

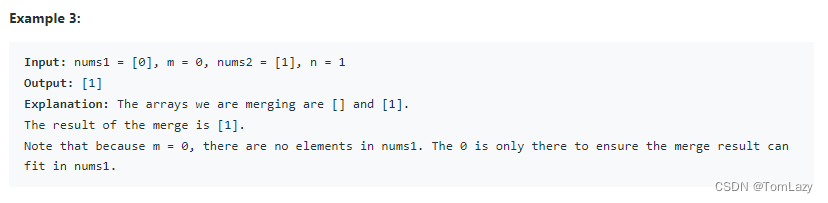
【条件约束】：

【跟踪】：

【Translate】：你能想出一个运行时间为O(m + n)的算法吗?

2. 题解

2.1 Arrays.sort()

这应该可以算是最简单的做法了，将num2的数加入到num1后，直接使用内置函数。

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        for (int i = 0; i < n; i++){
            nums1[m+i] = nums2[i];
        }
        Arrays.sort(nums1);
    }
}
1
2
3
4
5
6
7
8

2.2 循序比较+补足 O(m + n)

原题解来自于 jiuwanli 的 My clean java solution。 看来这个题解我突然发现，一开始我忽略了一个重要条件，就是num1和num2其实是已经排好序的递增数组，那么我们直接从最后开始比较就好啦，谁大谁后，最后如果n > m，那么再来一轮循环，顺序填入num1即可。

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int tail1 = m - 1, tail2 = n - 1, finished = m + n - 1;
        while (tail1 >= 0 && tail2 >= 0) {
            nums1[finished--] = (nums1[tail1] > nums2[tail2]) ? 
                                 nums1[tail1--] : nums2[tail2--];
        }

        while (tail2 >= 0) { //only need to combine with remaining nums2, if any
            nums1[finished--] = nums2[tail2--];
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13