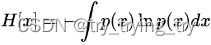近似熵 样本熵 模糊熵

特征提取field

表征信号序列复杂程度的无量纲指标，熵值越大代表信号复杂度越大。
应用：机械设备状态监测、故障诊断以及心率、血压信号检测
优点：抵抗环境干扰

1. 近似熵

Def: 近似熵(Approximate Entropy，ApEn)
提出：由 Steven M. Pincus 于 1991年从衡量信号序列复杂性的角度提出的[1]，用于度量信号中产生新模式概率的大小
Using: 越复杂的时间序列对应的近似熵越大，越规则的时间序列对应的近似熵则越小。
理解：为求取一个时间序列在模式上的自相似程度。对于一个信号序列的变化，可以利用近似熵值的改变达到有效识别的目的。

数学含义：

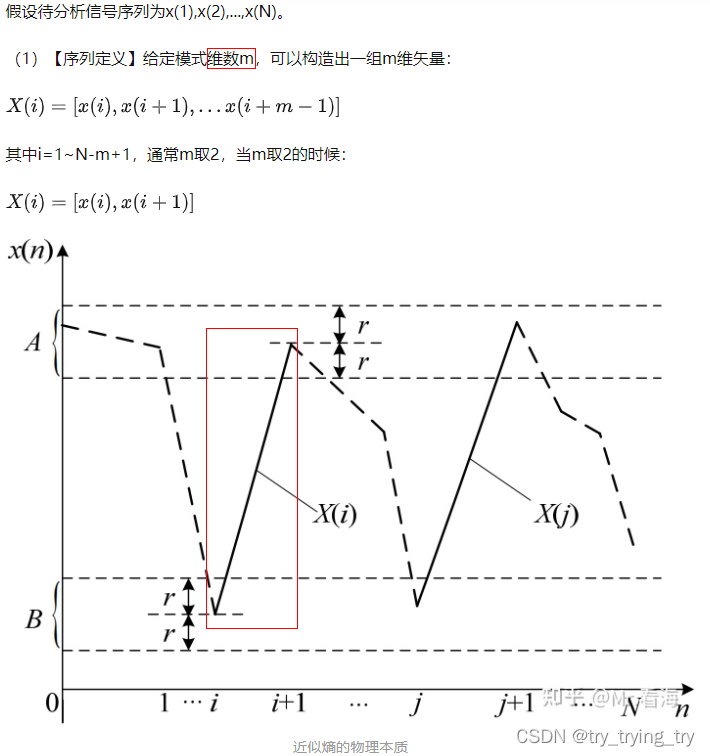
如果X(j)的对应端点都在容限范围内，则认为2维特征向量X(i)和X(j)的模式在r下近似。

物理本质：衡量当维数变化时信号序列中新模式出现的对数条件概率均值，因此理论上近似熵在表征信号序列的不规则性和复杂性方面具有较大的意义。
特点：
参考1 知乎

2. 样本熵

对近似熵算法的改进

Def: 样本熵（Sample Entropy）
提出：Richman等人提出的一种与近似熵不同的不计数自身匹配的统计量

数学含义：

参考1 知乎
参考2 csdn

3. 模糊熵

模糊熵和样本熵物理意义相似，都是衡量时间序列在维数变化时产生新模式的概率的大小。

Def: 模糊熵（Fuzzy Entropy）
提出：陈伟婷在2007年
应用：初衷是用于肌电型号处理中，不过其后在故障诊断、图像处理等领域

数学含义：

特点：

参考1 知乎
参考 csdn

=======

4. 熵

在信息论中，熵是接收的每条消息中包含的信息的平均量。-信息熵 --概率分布
熵越高，则能传输越多的信息
热力学熵：系统的宏观测定，并没有涉及概率分布
香农熵：(1948年，克劳德·艾尔伍德·香农将热力学的熵，引入到信息论)

Def
离散r.v

信息熵/负熵-香农

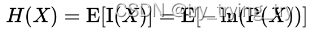
I(X) 是X 的信息量（又称为自信息）I(x)=−logP(x)，自信息只处理单个的输出。
但是其取值恒为正.由于信息的接受就是不肯定性的消除，即熵的消除（此处的熵取“热力学熵”中“熵”的含义），所以信息熵才常被人称作负熵。

熵的单位
单位取决于定义用到对数的底。当b = 2，熵的单位是bit；当b = e，熵的单位是nat；而当b = 10,熵的单位是 Hart。

5. 微分熵

参考 csdn最全各种熵