2022祥云杯---Crypto

水平太烂，只能搞出来一道题

little little fermat

题目：

from Crypto.Util.number import *
from random import *
from libnum import *
import gmpy2
from secret import x
 
flag = b'?????????'
m = bytes_to_long(flag)
def obfuscate(p, k):
    nbit = p.bit_length()
    while True:
        l1 = [getRandomRange(-1, 1) for _ in '_' * k]
        l2 = [getRandomRange(100, nbit) for _ in '_' * k]
        l3 = [getRandomRange(10, nbit//4) for _ in '_' * k]
        l4 = [getRandomRange(2, 6) for _ in '_' *k]
        A = sum([l1[_] * 2 ** ((l2[_]+l3[_])//l4[_]) for _ in range(0, k)])
        q = p + A
        if isPrime(q) * A != 0:
            return q
 
p = getPrime(512)
q = obfuscate(p, 5)
e = 65537
n = p*q
print(f'n = {n}')
 
assert 114514 ** x % p == 1
m = m ^ (x**2)
c = pow(m, e, n)
print(f'c = {c}')
 
'''
n = 141321067325716426375483506915224930097246865960474155069040176356860707435540270911081589751471783519639996589589495877214497196498978453005154272785048418715013714419926299248566038773669282170912502161620702945933984680880287757862837880474184004082619880793733517191297469980246315623924571332042031367393
c = 81368762831358980348757303940178994718818656679774450300533215016117959412236853310026456227434535301960147956843664862777300751319650636299943068620007067063945453310992828498083556205352025638600643137849563080996797888503027153527315524658003251767187427382796451974118362546507788854349086917112114926883
'''

题目里的fermat暗示与费马定理有关。看p、q的生成过程，可以大概猜出pq是相近的，至于obfuscate里while循环里的内容看不太懂。用yafu工具试着分解一下n，就得到了。再用基础方法解rsa，得到m。

再看这句， 

assert 114514 ** x % p == 1

 ==》

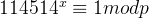
由费马定理可以推出x = p-1，故把上面得到的m与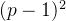异或一下即为最终flag，总体代码如下：

from gmpy2 import *
from Crypto.Util.number import *
 
e = 65537
n = 141321067325716426375483506915224930097246865960474155069040176356860707435540270911081589751471783519639996589589495877214497196498978453005154272785048418715013714419926299248566038773669282170912502161620702945933984680880287757862837880474184004082619880793733517191297469980246315623924571332042031367393
c = 81368762831358980348757303940178994718818656679774450300533215016117959412236853310026456227434535301960147956843664862777300751319650636299943068620007067063945453310992828498083556205352025638600643137849563080996797888503027153527315524658003251767187427382796451974118362546507788854349086917112114926883
 
p = 11887853772894265642834649929578157180848240939084164222334476057487485972806971092902627112665734648016476153593841839977704512156756634066593725142934001
q = 11887853772894265642834649929578157180848240939084164222334476057487485972806971092902627112665734646483980612727952939084061619889139517526028673988305393
d = invert(e,(p-1)*(q-1))
m = pow(c,d,n)
 
flag = m ^ (p-1)**2
print(long_to_bytes(flag))