队列（queue）

队列基础知识

我们通过和栈的比较进行学习队列知识。
栈（stack）：一种后进先出（LIFO）的线性表，只允许在一端进行插入和删除，这一端交栈顶，另一端交栈底，没有数据的叫做空栈。
队列（queue）：一种先进先出(FIFO)的线性表，只允许在表的一端进行插入，在另一端进行删除，允许插入的一端叫做队尾，允许删除的一端叫做队头。（示例：排队）
队列与栈相同，也应该有两种实现方式：用顺序表实现的叫顺序队列，用链表实现的叫链式队列。但是在这里，我们用顺序表实现的不叫顺序队列，而叫循环队列。
栈：
顺序栈：入栈时间复杂度O（1），出栈时间复杂度O（1）.
链栈：入栈时间复杂度O（1），出栈时间复杂度O（1）.

循环队列

现在我们用顺序表实现队列：队列要求一端插入，另一端删除：我们用顺序表实现则会有两种可能性：1）头插尾删
插入时间复杂度O（n）,删除时间复杂度O（1）.
2）头删尾插，
插入的时间复杂度O（1），删除的时间复杂度O（n）.
很显然两种可能均不可能都让时间复杂度为O（1），为此我们做一修改，这也是为什么顺序队列一般叫做循环列表。
修改：我们不移动数据，而去移动队头指针和队尾指针，这样就可以让时间复杂度为O（1）。然而循环的概念又从何而来呢，很显然根据上面移动头指针的方式，将会浪费前面的内存，因此我们将队头和队尾连接起来，设置成一个环形，这样也就避免了浪费，连起来也就得到了所谓的循环概念。

链式队列

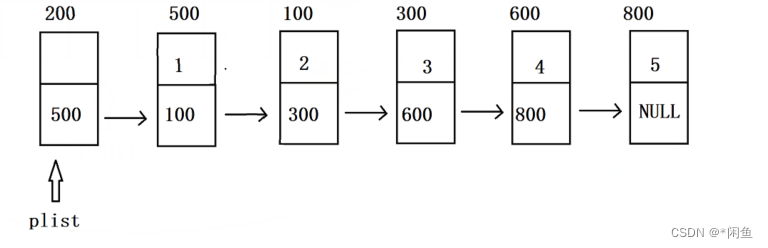
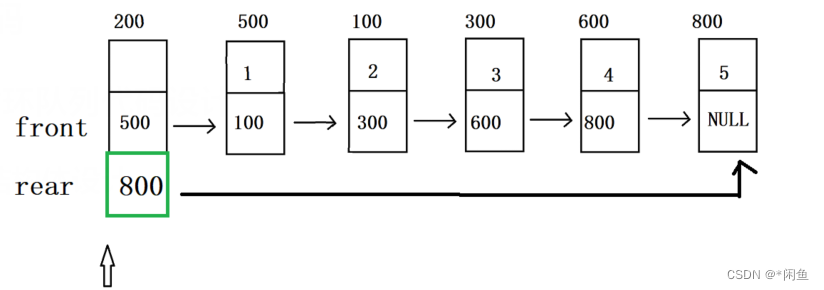
假如只是用单链表去实现链式队列，则队尾插入（尾插），队头出（头删），这时，我们会要求头删的时间复杂度O(1),尾插的时间复杂度为仍为O(1),但是如果是上述单链表，找到尾结点需要遍历整个单链表，尾插的时间复杂度为O(n),很显然不符合要求为此做一修改，

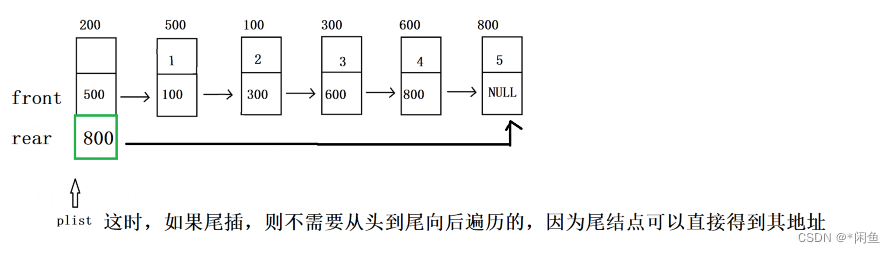
如上图修改：头节点增加一个指向尾结点的指针域，去掉原来为空的数据域，这样我们尾删时便可以直接通过头结点的rear指针找到尾结点，直接进行尾删，时间复杂度为O(1).

问题实例

循环队列问题实例

示例一：约瑟夫环问题
问题：据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。
示例二：魔方阵
在《射雕》中郭黄二人被裘千仞追到黑龙潭，躲进瑛姑的小屋。瑛姑出了一道题：数字1~9填到三行三列的表格中，要求每行、每列、及两条对角线上的和都相等。这道题难倒了瑛姑十几年，被黄蓉一下子就答出来了。
4 9 2
3 5 7
8 1 6
方法：(1) 将1放在第一行中间一列;
(2) 从2开始直到n×n止各数依次按下列规则存放：
按 45°方向行走，如向右上
每一个数存放的行比前一个数的行数减1，列数加1
(3) 如果行列范围超出矩阵范围，则回绕。
例如1在第1行，则2应放在最下一行，列数同样减1;
(4) 如果按上面规则确定的位置上已有数，或上一个数是第1行第n列时，
则把下一个数放在上一个数的下面。

队列设计思路

循环队列设计思路

循环队列有三个难点（因为是循环的所以没办法扩容，必须一次性申请够格子数）
1）如何和保证顺序表实现的队列入队和出队的时间复杂度都为O（1）？
方法：让数据不动，让队头指针和队尾指针移动，然后又为了使用到队列前面的空闲空间，则让队头和队尾链接成一个整体，则这种头尾相连的顺序存储结构称为循环队列。

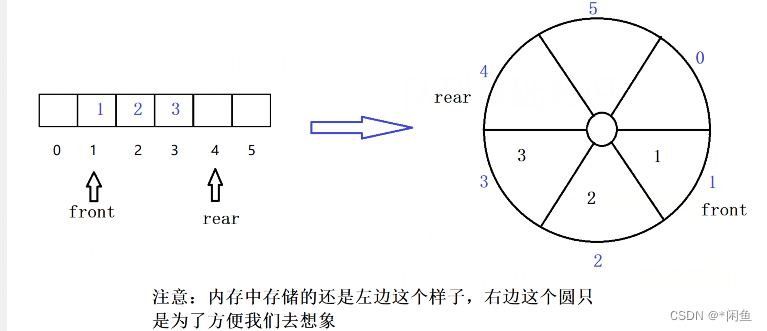
2）因为难点1，我们让头尾相连，且数据不动指针动，这样我们就会发现一个问题，判空条件和判满条件冲突了，
判空条件：rear == front
判满条件：rear == front
解决方案：加标记
第一方案：结构体设计的时候，额外加一个成员，加一个有效长度length,则使用第一种方案，
判空条件：fron t== rear&&length== 0
判满条件：front== rear&&lengeh!=0
第二方案：在队尾处房费一个空间不用，作为标记去使用，则使用第二种方案：
判空条件：front==rear
判满条件：队尾指针，向后再走一步，就遇到了队头，则认为满了
在队尾处浪费一个空间不用，作为标记去使用
3）因为我们将顺序表实现的队列，臆想成环形，头尾相连，这样怎么求循环队列中有多少个有效元素？（怎么求有效长度）
两种情况：
第一种：rear>front

第二种：rear
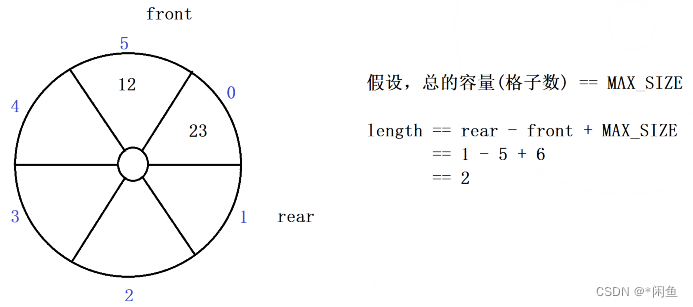
我们计算有效长度便要将这两种方法整合在一块，（MAX_SIZE为总容量）
总公式：length=(rear-front+MAX_SIZE)%MAX_SIZE
+MAX_SIZE：防止rear-front出现负数，
%MAX_SIZE：防止rear-front没有出现负数，导致MAX_SIZE加多了

链式队列设计思路

初始化：
首先我们的结构体设计分为头节点个有效结点，初始化只需要初始化头节点，因为没有有效结点，头结点的两个指针域都为NULL
入队：（尾插）
1）普通情况：队列中存在有效结点

2）特殊情况：队列中没有数据，也就是插入的第一个数据既是第一个有效结点也是尾结点。

出队：（头删）
1）普通情况（队列中有大于一个有效数据）

只需要将头节点指向第二个有效结点，然后释放第一个有效结点即可
2）特殊情况：只有一个有效结点

根据上图，删除的方式便是头节点的两个指针域都为NULL，释放第一个有效结点

代码

循环队列代码设计

结构体设计

typedef int ELEM_TYPE;
#define MAX_SIZE 100

typedef struct Queue
{
	ELEM_TYPE *base;//用来接收malloc在堆内申请的连续内存，用于分配空间
	int front;//队头指针，若队列不空，则指向队头元素
	int rear;//队尾指针，若队列不空，则指向队列尾元素的下一个位置

	//int length;//用于第二个难点：用于区分判空判满条件
}Queue, *PQueue;
1
2
3
4
5
6
7
8
9
10
11

函数实现

//初始化
void Init_queue(struct Queue* qu)
{
	assert(qu != NULL);

	qu->base = (ELEM_TYPE*)malloc(MAX_SIZE * sizeof(ELEM_TYPE));
	assert(qu->base != NULL);

	qu->front = qu->rear = 0;

}

//入队
bool Push(struct Queue* qu, ELEM_TYPE val)
{
	assert(qu != NULL);
	if (Is_Full(qu))
	{
		return false;
	}

	qu->base[qu->rear] = val;
	qu->rear = (qu->rear + 1) % MAX_SIZE;//队尾指针注意不要忘记向后走一步，但是不能用++

	return true;
}

//出队
bool Pop(struct Queue* qu) {
	assert(qu != NULL);
	if (Is_Empty(qu))
	{
		return false;
	}
	qu->front = (qu->front + 1)% MAX_SIZE;
	return true;
}

//获取队头元素值
ELEM_TYPE Front(struct Queue* qu) {
	assert(qu != NULL);
	if (Is_Empty(qu))
	{
		printf("error!!!");
		exit(1);
	}
	return qu->base[qu->front];
}

//搜索
int Search(struct Queue* qu, ELEM_TYPE val) {
	assert(qu != NULL);
	for (int i = qu->front; i != qu->rear; i=(i+1)%MAX_SIZE) {
		if (qu->base[i] == val) {
			return i;
		}
	}
	return NULL;
}

//判空
bool Is_Empty(struct Queue* qu) {
	return qu->front==qu->rear;
}

//判满
bool Is_Full(struct Queue* qu) {
	return(qu->rear + 1)%MAX_SIZE == qu->front;
}

//获取有效值个数
int Get_length(struct Queue* qu) {
	/*
	int count=0; 
	for (int i = qu->front; i != qu->rear; i=(i+1)%MAX_SIZE) {
		count++;
	}
	*/
	return (qu->rear-qu->front+MAX_SIZE)%MAX_SIZE;
}

//清空
void Clear(PQueue qu) {
	qu->front = qu->rear = 0;//等不等于0均可
}

//销毁
void Destroy(PQueue qu) {
	free(qu->base);
	qu= NULL;
}

//打印
void Show(PQueue qu) {
	assert(qu!=NULL);
	for (int i = qu->front; i < qu->rear; i++) {
		printf("%d ",qu->base[i]);
	}
	printf("\n");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

链式队列代码设计

结构体设计

//链式队列有效节点结构体设计（一个数据域+一个指针域）
typedef struct Node
{
	ELEM_TYPE data;//数据域
	struct Node* next;//指针域
}Node;


//链式队列头结点结构体设计（二个指针域）
typedef struct List_Queue
{
	struct Node* front;//队头指针
	struct Node* rear;//队尾指针
}List_Queue;
1
2
3
4
5
6
7
8
9
10
11
12
13
14

函数实现

//初始化
void Init_list_queue(struct List_Queue* lqu)
{
	assert(lqu != NULL);
	lqu->front = NULL;
	lqu->rear = NULL;
}

//入队（尾插）
bool Push(struct List_Queue* lqu, ELEM_TYPE val)
{
	assert(lqu != NULL);
	//1.购买新节点
	struct Node* pnewnode = (struct Node*)malloc(sizeof(struct Node));
	assert(pnewnode != NULL);
	pnewnode->data = val;


	//2.分情况，进行插入，首先处理特殊情况：空队列时，进行入队
	if (Is_Empty(lqu))
	{
		pnewnode->next = NULL;
		lqu->front = lqu->rear = pnewnode;

		return true;
	}

	//3.普通情况(队列中已经有数据)
	//插入到尾节点后面(尾结点地址由rear指针保存)
	pnewnode->next = lqu->rear->next;
	lqu->rear->next = pnewnode;

	//注意：队尾指针需要重新指向
	lqu->rear = pnewnode;

	return true;
}

//出队（头删）
bool Pop(struct List_Queue* lqu)
{
	assert(lqu != NULL);
	if (Is_Empty(lqu))
	{
		return false;
	}

	//1.用指针p指向待删除节点
	struct Node* p = lqu->front;


	//2. 分情况处理，先处理特殊情况：删除的是仅剩下的唯一一个有效节点
	if (p->next == NULL)
	{
		free(p);
		lqu->front = lqu->rear = NULL;
		return true;
	}

	//3.剩下的就是普遍情况(队列中有效节点的个数>=2，就是不仅一个)
	//用指针q指向待删除节点的上一个节点
	//可以用lqu代替q

	//3.跨越指向
	lqu->front = p->next;

	//4.释放节点
	free(p);

	return true;

}

//获取队头元素值
ELEM_TYPE Front(struct List_Queue* lqu)
{
	assert(lqu != NULL);
	if (Is_Empty(lqu))
	{
		printf("error\n");
		exit(1);
	}

	return lqu->front->data;

}

//搜索
struct Node* Search(struct List_Queue* lqu, ELEM_TYPE val)
{
	//不需要前驱的for循环
	struct Node* p = lqu->front;

	for (; p != NULL; p = p->next)
	{
		if (p->data == val)
		{
			return p;
		}
	}

	return NULL;
}

//判空
bool Is_Empty(struct List_Queue* lqu)
{
	return lqu->front == NULL;
}

//判满 //链式队列不存在判满


//获取有效值个数
int Get_length(struct List_Queue* lqu)
{
	//不需要前驱的for循环
	int count = 0;

	struct Node* p = lqu->front;
	for (; p != NULL; p = p->next)
	{
		count++;
	}

	return count;
}

//清空
void Clear(struct List_Queue* lqu)
{
	Destroy1(lqu);
}

//销毁1 //无限头删
void Destroy1(struct List_Queue* lqu)
{
	while (lqu->front != NULL)
	{
		Pop(lqu);
	}
}
//销毁2 //不借助头结点，但是需要两个临时指针p和q
void Destroy2(struct List_Queue* lqu)
{
	//assert
	struct Node* p = lqu->front;
	struct Node* q = NULL;

	lqu->front = lqu->rear = NULL;

	while (p != NULL)
	{
		q = p->next;
		free(p);
		p = q;
	}

}

//打印
void Show(struct List_Queue* lqu)
{
	//不需要前驱的for循环
	struct Node* p = lqu->front;
	for (; p != NULL; p = p->next)
	{
		printf("%d ", p->data);
	}
	printf("\n");

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172