-
【红黑树】都这样讲了，不会还有人不会红黑树吧
1. 简介红黑树 and 红黑树的性质
我们在前面学习过二叉树，而二叉树有被简单的分为普通二叉树，二叉搜索树，完全二叉树，二叉平衡树等，在二叉搜索树中包含有 AVL树，红黑树。博主在以前的文章中写过AVL树的相关内容，有兴趣的读者可以去康康，直接甩链接(124条消息) 【数据结构高阶】终于有人把AVL树给说清了_小小怪下士～的博客-CSDN博客
我们学习过AVL树的同学们都知道，AVL树是一个绝对平衡的二叉树，
所谓的绝对平衡说的就是一个节点的左右子树的高度之差的绝对值是不能超过1的，我们同时也知道这个AVL树主要是被用于查找元素的，为了提高查找元素的效率我们才让它绝对平衡，这样它的查找元素的时间复杂度就为O(logn)，它中添加和删除元素的时候，就显得格外吃力了。于是我们今天介绍一个我们的红黑树，这个特殊的二叉树其实也是一个平衡树，但是没有AVL树那么的绝对，它是相对平衡的。
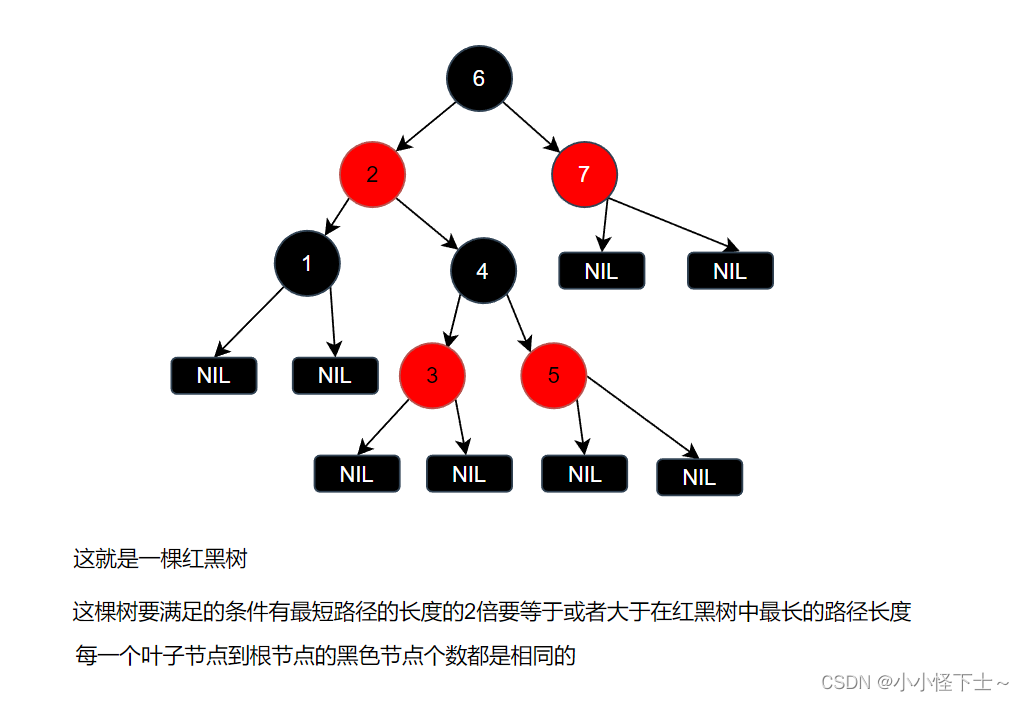
有关于红黑树的性质：
-
每个节点要么是黑色，要么是红色
-
根节点永远是黑色的
-
每个叶子节点(NIL)是黑色的
-
每个红色节点的两个子节点一定都是黑色，不能有两个红色节点相连
-
任意一个节点到每个叶子节点的路径都包含相同数量的黑色节点
-
如果一个节点是黑色的，那么这个节点肯定存在两个子节点
2. 在红黑树中操作元素
2.1 在红黑树中查找一个元素
其实这里所谓的红黑树也就是一个变得较为平衡的二叉搜索树，但是这个平衡没有AVL树那么的绝对平衡。也就是因为这一点，我们这里的红黑树的查询效率会比AVL树稍逊一筹。原因还是归结于红黑树不是那么严格平衡的二叉树，它要求树中的最大的遍历路径要小于树中最短遍历路径的2倍。
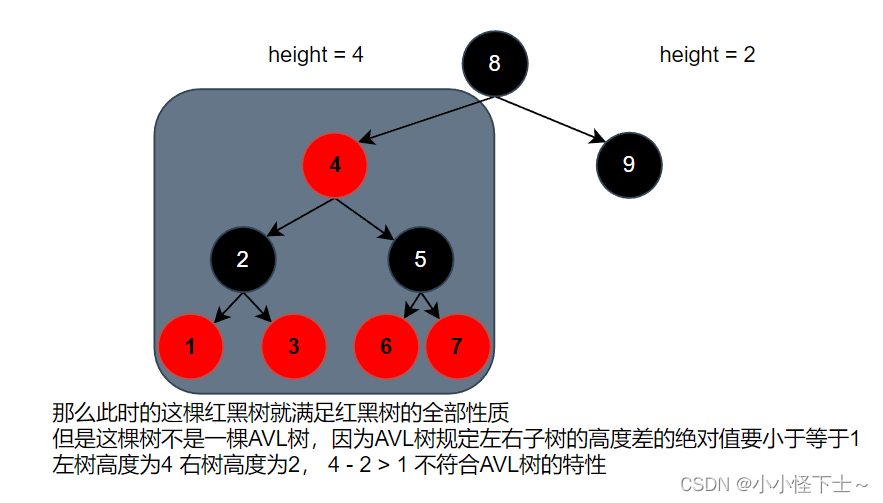
说起查找元素还是和普通的二叉搜索树是一样的。就还是那上面的这张图来说，就比如我现在要在红黑树中查找
7这个元素：即从根节点看是找到，8 > 7，那么就要左子树中寻找，然后遇到了4,4 < 7 去右子树中寻找，接着又遇到了5,5 < 7 ，又去右子树中寻找，紧接着就碰到了7， 7 == 7 那么此时就找到了元素。其实在红黑树中查找元素的最好效率就是O(logn)，这就是当每个节点的最右子树的是平衡的，那么此时的红黑树就变成了AVL树。总之呢，AVL树的查找效率 >= 红黑树的查找效率 （=:红黑树变成了AVL树）
2.2 在红黑树中插入元素
那么就下来就介绍一个红黑树的插入喽❤️❤️❤️❤️❤️❤️
插入操作大致分为这两个步骤：
- 查找插入位置(在插入元素的时候，还是涉及查找滴😏😏😏)
- 插入后自平衡(还记着博主说的红黑树的性质吗，我们在插入节点的时候，可不能违背它们哦)
那么我们分析一下，我们要在红黑树树中要插入什么颜色的节点呢?
咦??为什么会有这个问题，有些同学就会问红黑树 红黑 红黑，就是插入 红色和黑色的节点呀，我想插什么颜色，就插什么颜色。其实这样是不行的，那么就同学们分别看看在一个红黑树中插入红色节点和黑色节点的时候，到底会遇到什么情况?
在插入一个黑色节点的时候图例：
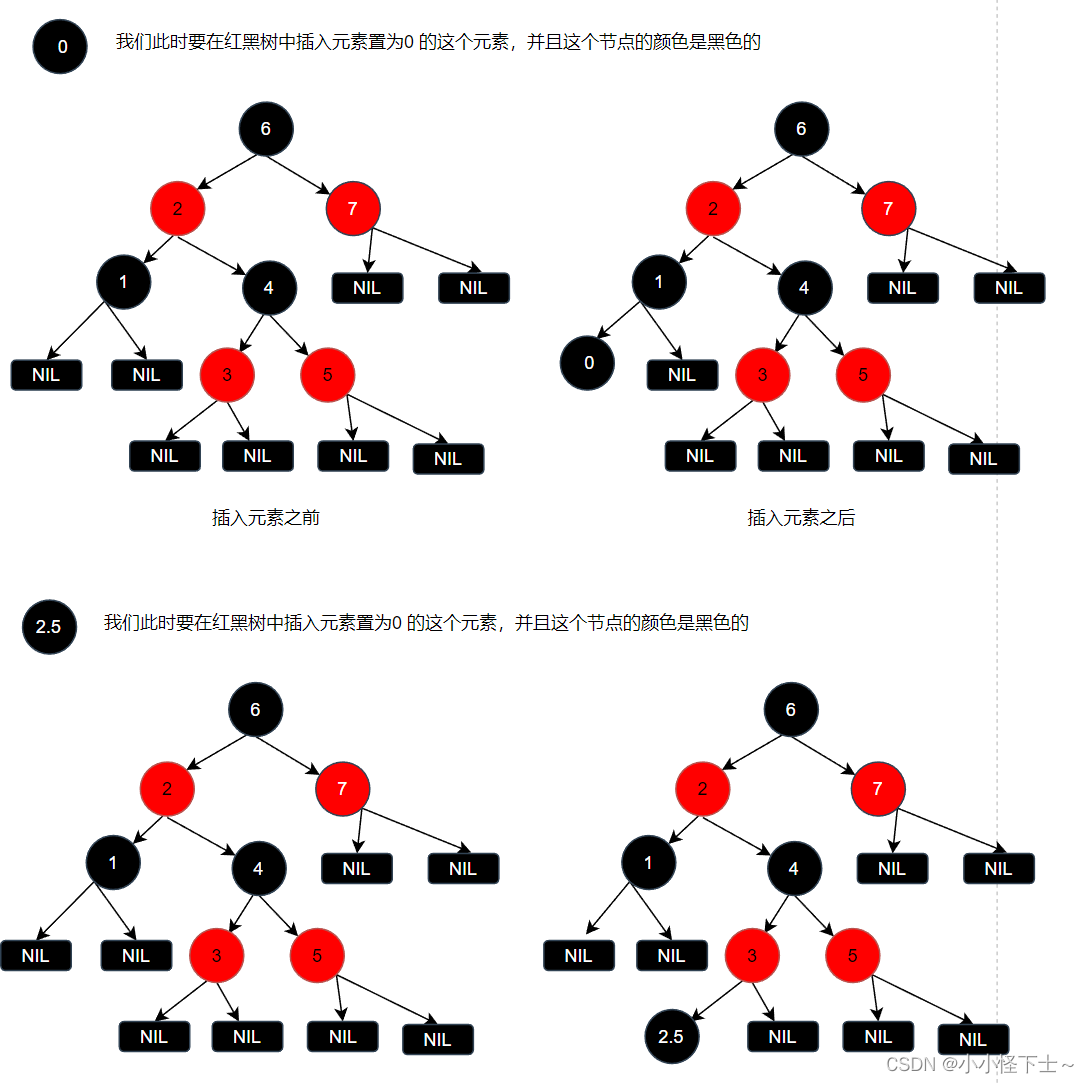
老铁们请看第一种情况：我们在红黑树中插入了颜色为黑色的，值为0的节点，它的父亲节点是黑色的。但是大家此时看看看一下每个叶子节点到根节点上的黑节点的个数是多少？很明显我们在添加0这个节点的路径上比其他的路径上的黑色节点要多一个。那么就不符合红黑树的性质。
第二种情况，我在红黑树中添加了一个值为2.5的黑色节点，但是我们在比较一下，这个节点插入的路径上的黑色节点是不是要比其他路径上的黑色节点要多出一个。那么也不符合红黑树的形式。
在插入一个红色节点的时候图例：
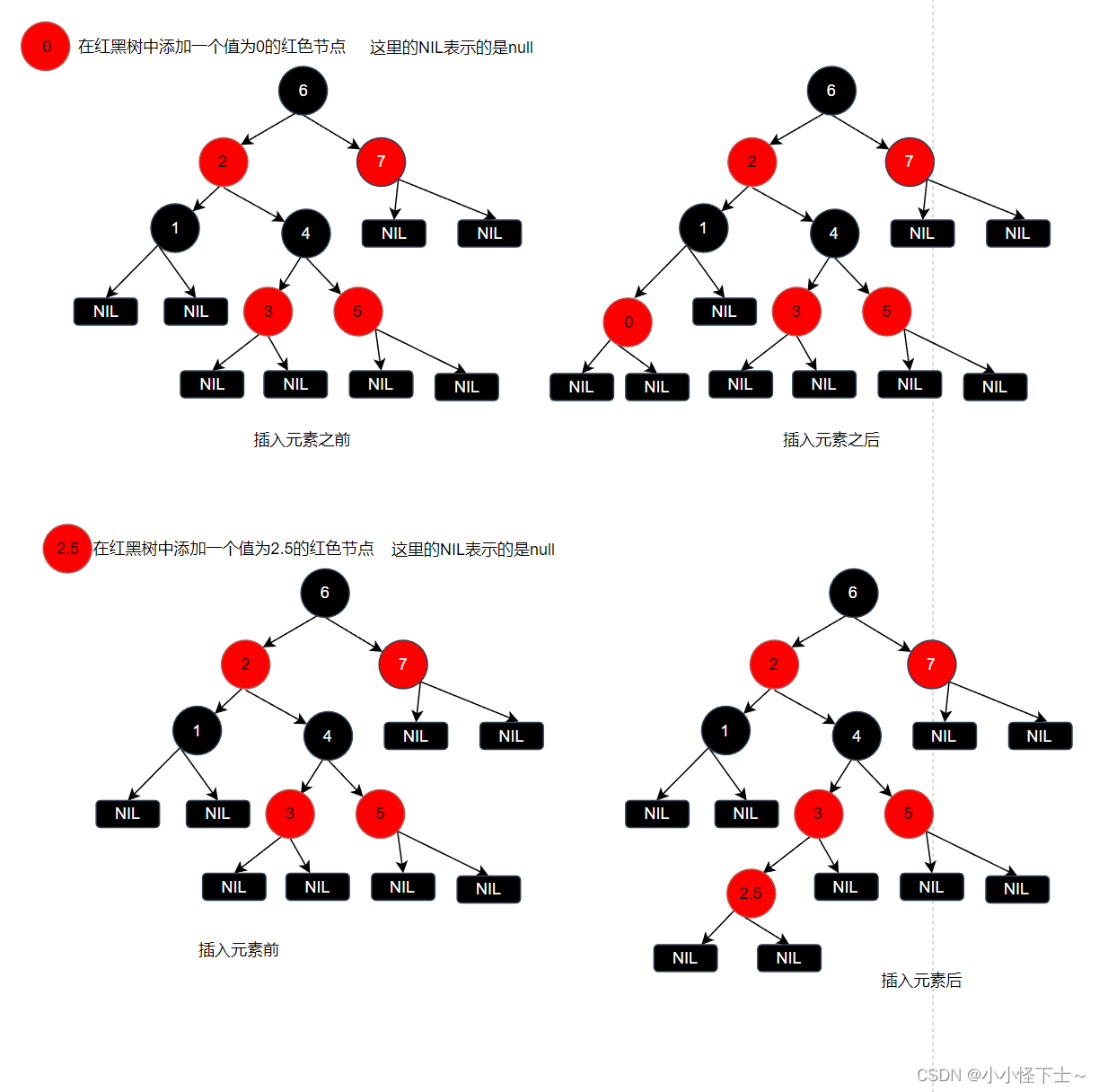
第一种情况： 我们在红黑树中插入了一个值为0的红色节点，可以看出这个红色的节点就直接添加到了值为1的黑色节点的左面。那么我们在看看在插入元素之后，是否满足原本红黑树的性质，答案是满足的。
第二中情况： 我们在红黑树中插入一个值为2.5的红色节点，这个节点被添加到了值为3的红色节点的左面。那么我们再看看在插入元素之后，是否满足红黑树的性质?其实还是有一点不满足的，那就是不能有两个红色的节点相连。这样就破坏了红黑树的特性，那么此时就要进行左旋或者右旋。
其实这里会有许多的同学会问，为什么会有这些条条框框的束缚，其实这是因为我们要提高红黑树的插入元素和删除元素的效率。PS:就是把低于AVL树的那些查找效率给予了，插入和删除(详细在文末介绍)
**总结上述，我们在红黑树中插入节点的时候，插入节点的颜色必须为红色。**在插入红色节点之后，红黑树会自平衡，在自平衡的过程中就会改变节点的颜色。
总体来说在红黑树插入中有四种情况：第一种情况： 红黑树原本为空树，那么我们直接将插入的黑色节点设置为根节点
第二种情况： 插入节点的key已经存在了，不需要处理，我们在这是在添加元素的时候，其实这个元素是一个
RBNode其中的值是一个键值对类似于 (key,value)这样。如果我们在查找的插入节点位置的时候，遇到了相同的key，那么就直接用插入节点的value值覆盖以前节点的value值。
图示：
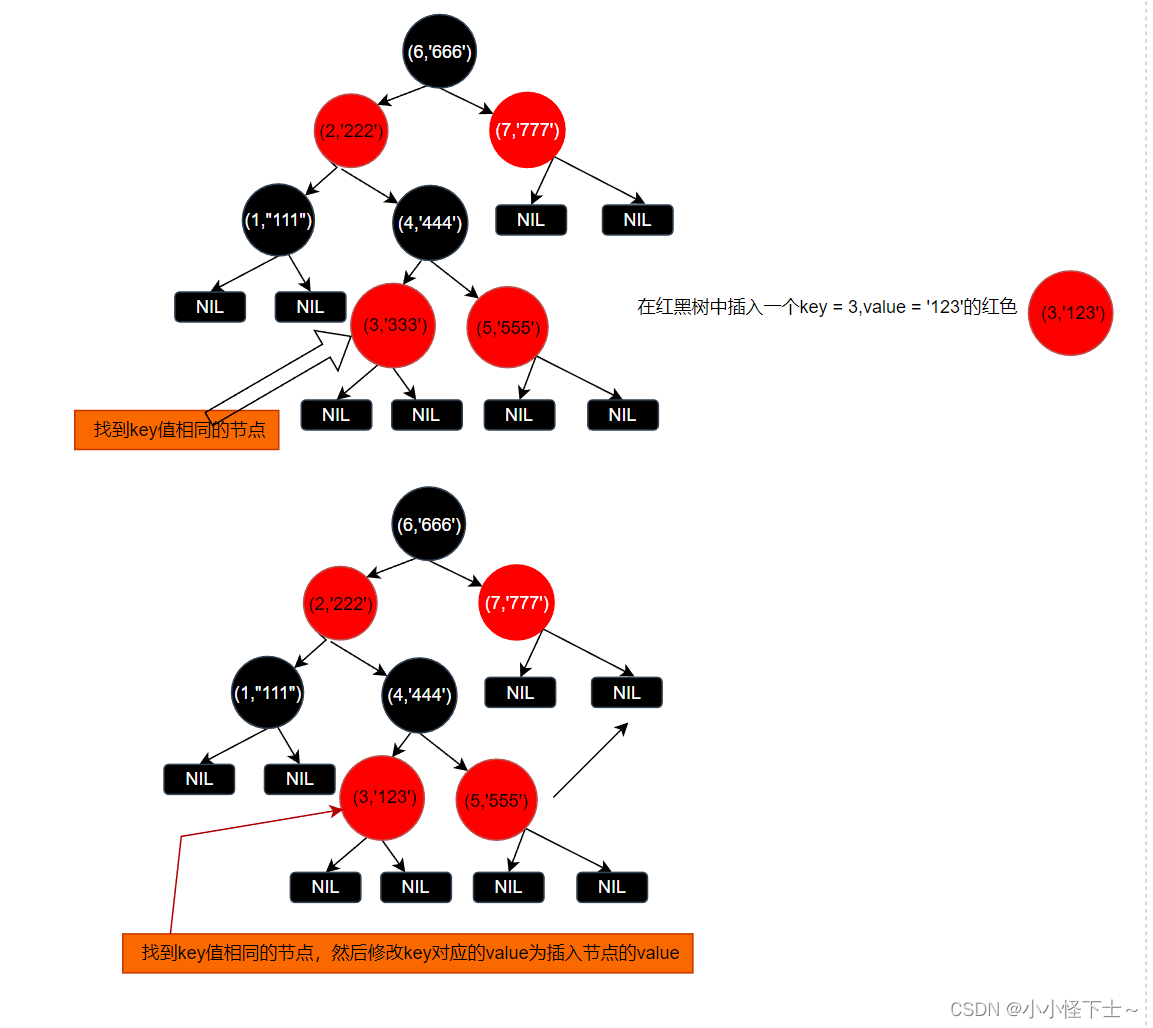
第三种情况： 插入节点的父亲节点为黑色节点，因为你插入的路径，黑色节点没有发生变化，所以红黑树依然平衡，所以不需要处理。
图示：
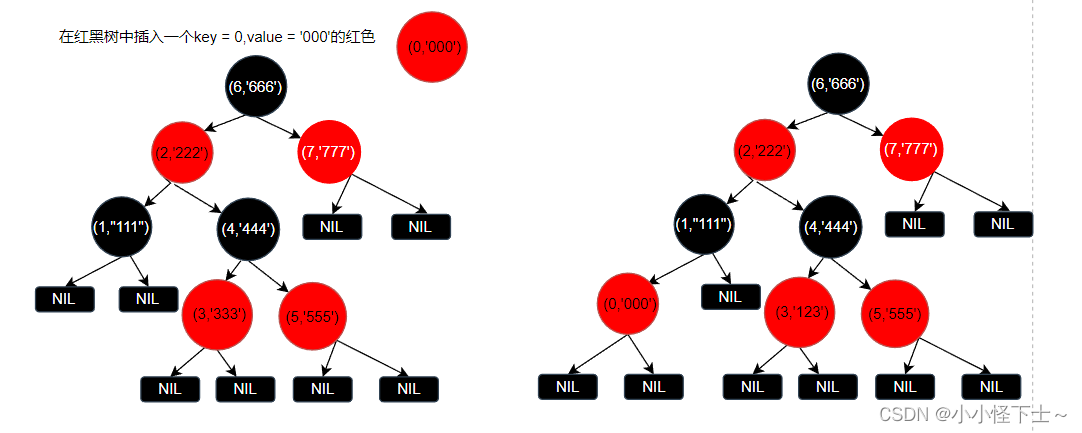
第四种情况：
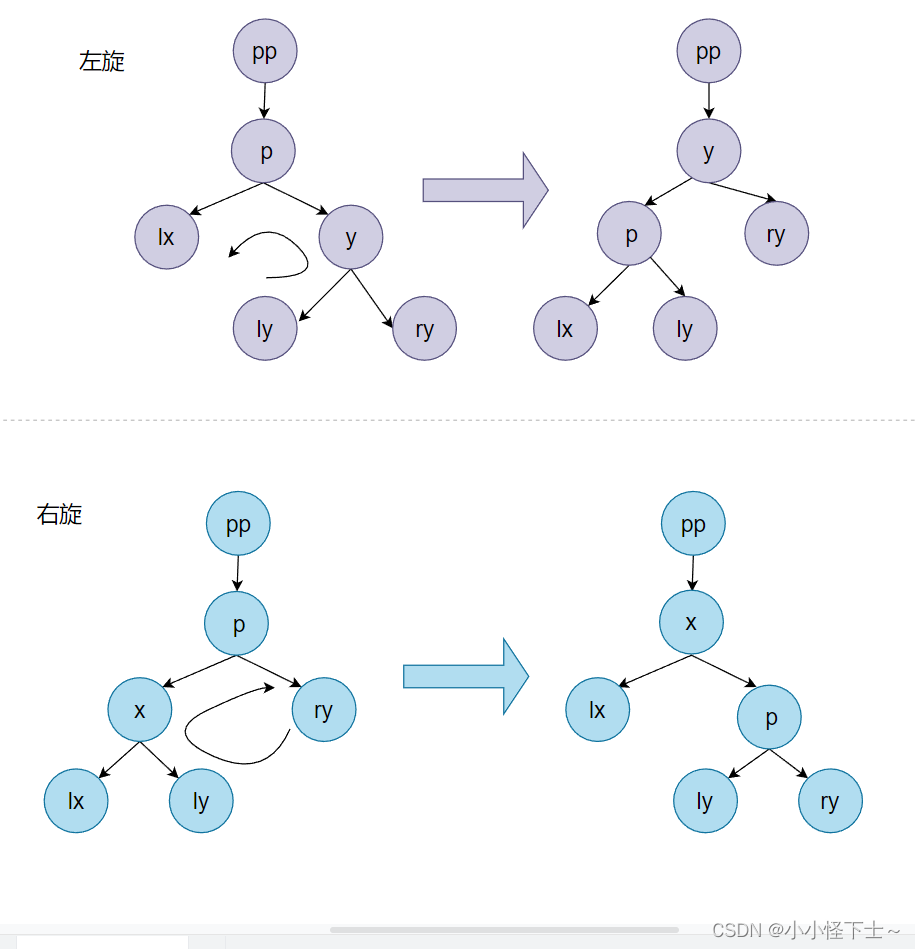
那么此时就要说一说我们的左旋和右旋了。
其实博主在AVL树中说过左旋和右旋，但是我觉得那里还是说的不够好，如果看AVL树那一块博文的读者在左旋后右旋方面有不会的，可以详细阅读以下的片段。
右旋：
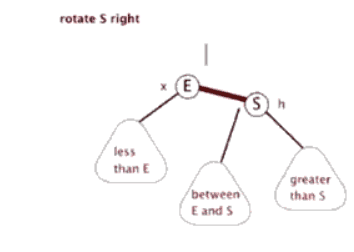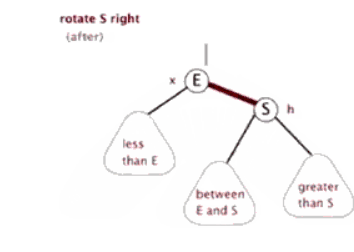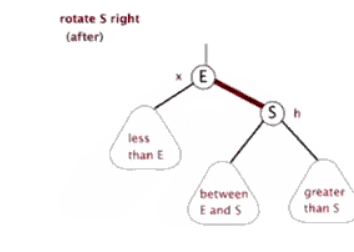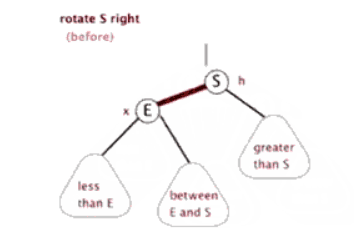
左旋：
在这里我们那左旋和右旋都举一个小栗子❤️❤️❤️：
情况4.1： 叔叔节点存在，并且为红色，还有就是父亲节点也为红色。
图例：
调整之前：
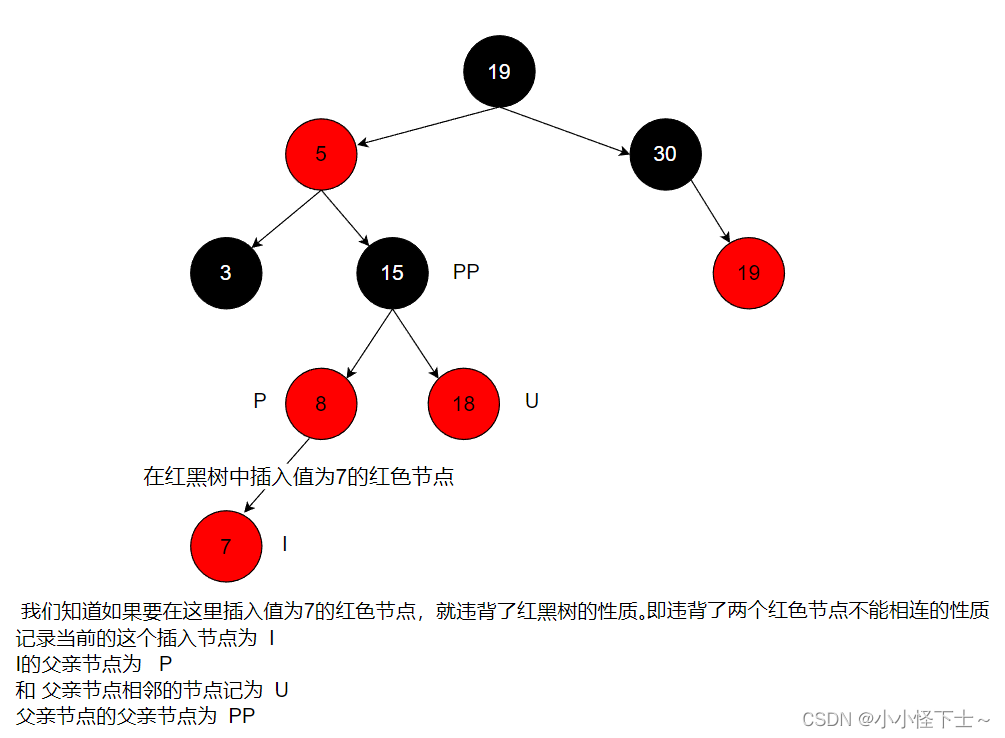
此时的解决办法：
将爸爸节点P和叔叔节点U染为黑色，将爷爷节点PP染为红色，并且在以爷爷节点为当前节点，进入下一轮处理。调整之后：
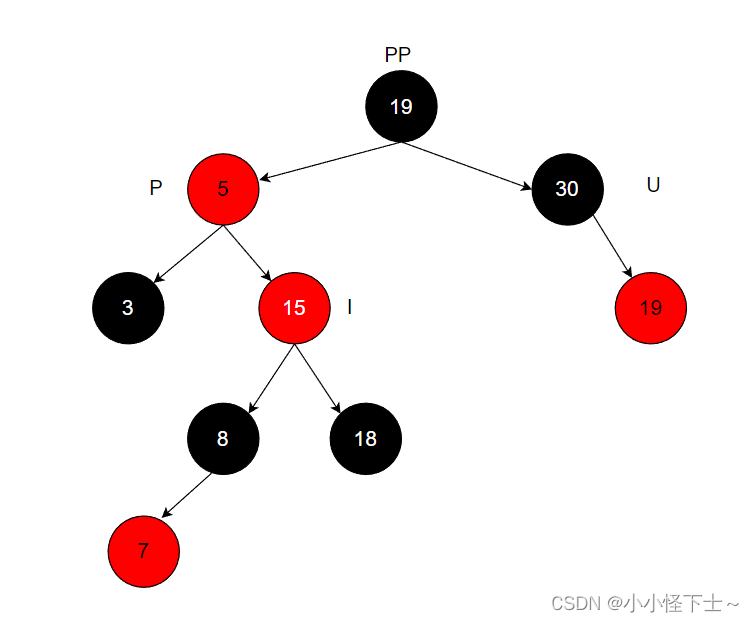
那么我们此时已经把这棵小的子树已经调整满足了红黑树的性质，那么此时就在把当前节点前上移动，
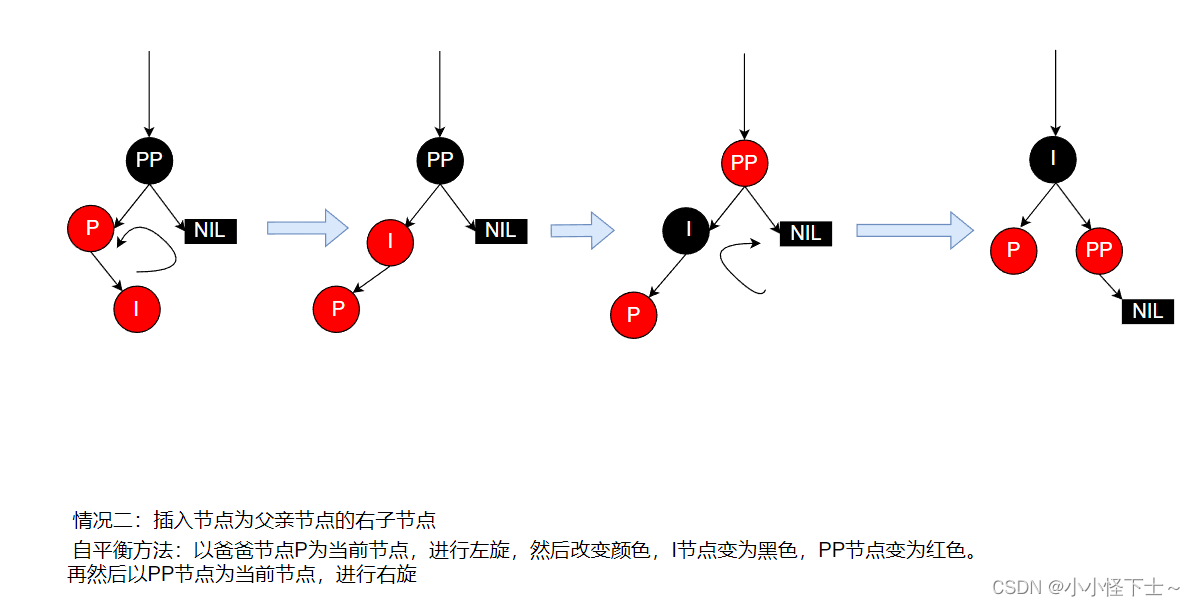
如果由于我们刚才的变色导致其他的节点违背了红黑树的性质，还需要进行调整。正如上图所示此时的爸爸节点 P 和 孩子节点 I 就产生冲突(在红黑树中两个红色节点不能相连)，但是此时的叔叔节点U 不是红色的，那么此时的这个情况就要另当别论了。情景4.2： 叔叔节点不存在或者为黑色节点，父亲节点为爷爷节点的左子树。
图例：
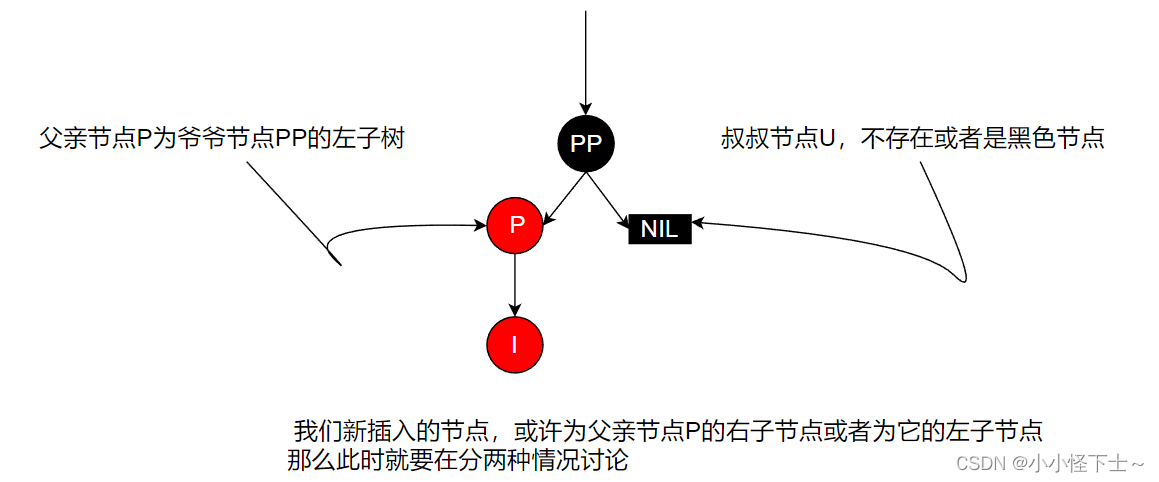
情况4.2.1： 插入节点为父亲节点的左子节点(LL双红)
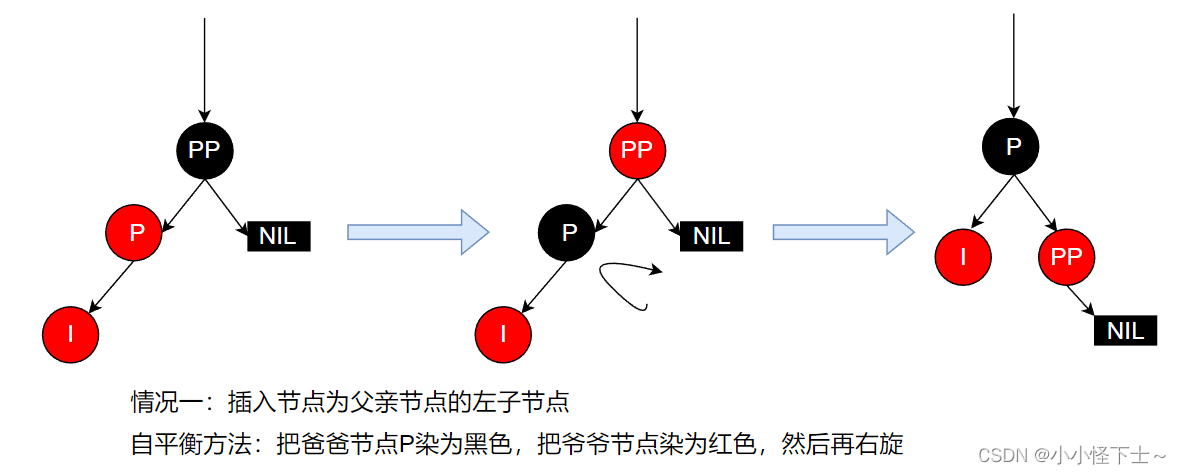
部分伪代码实现：
rightRotate() //1.得到通过插入节点得到爸爸节点 P 和 爷爷节点 PP,即插入节点为node RBNode P = parentOf(node); //parentOf()方法，通过此方法得到node的爸爸节点 RBNode PP = parentOf(parent); //2.变色 P.setColor(Black); PP.setColor(Red); //3.右旋 PP.left = P.right; //更新爷爷节点PP的左指向 if(P.right != null){ P.right.parent = PP; //更新爸爸节点的右子节点的父亲指向 } if(PP.parent != null){ //如果此时的PP.parent不为null，那么就说明此时的这个PP节点之下的树，只是一个子树而已 P.parent = PP.parent; //把爷爷节点原来的父亲之前赋给爸爸节点 if(PP.parent.left == PP){ PP.parent.left = P; }else if(PP.parent.right == PP){ PP.parent.right = P; } }else{ //此时的PP就是一棵树的根节点，于是直接调整根节点 this.root = P; this.root.parent = null; } //更新爷爷节点PP的指向,和爸爸节点P的指向 P.right = PP; PP.parent = P;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
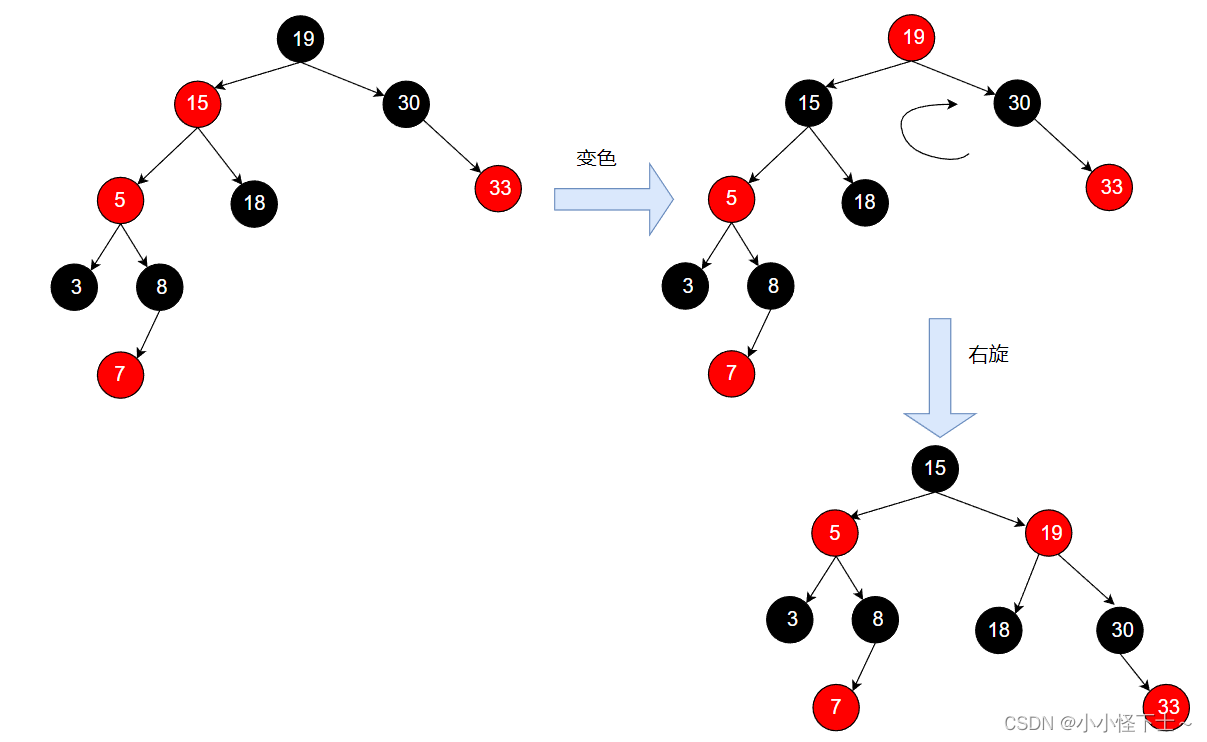
情景4.2.2：
部分代码：
//左旋 // p p // | | // x y // / \ / \ // lx y x ry // / \ / \ // ly ry lx ly private void leftRotate(RBNode x){ //x 节点表示的是当前节点，其实就是爷爷节点 PP RBNode y = x.right; //此时的y 就表示的是爸爸节点 P x.right = y.left; //调整x / PP节点的指向，为 y / P节点的右孩子 if(y.left != null){ y.left.parent = x; //y / P 节点的右孩子的父亲指向改变为 x / PP节点 } //此时的这个x作为头节点的一个树，其实是一棵子树 if(x.parent != null){ y.parent = x.parent; if(x == x.parent.left){ x.parent.left = y; }else{ x.parent.right = y; } }else{ //原来的x为根节点，那么就那y设置为root this.root = y; this.root.parent = null; } x.parent = y; y.left = x; //然后再调用右旋方法 rightRotate(x); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
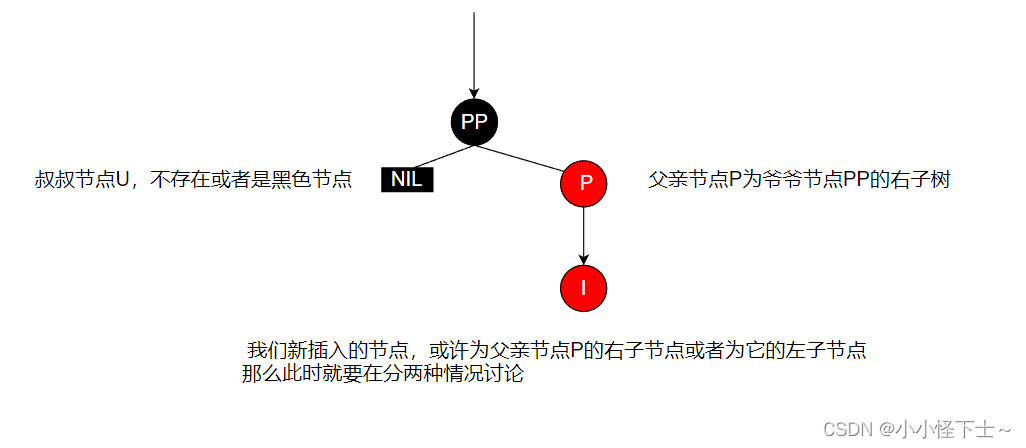
情景4.3： 叔叔节点U不存在，或者为黑色，父亲节点为爷爷节点的右子树
图例：
情况4.3.1：
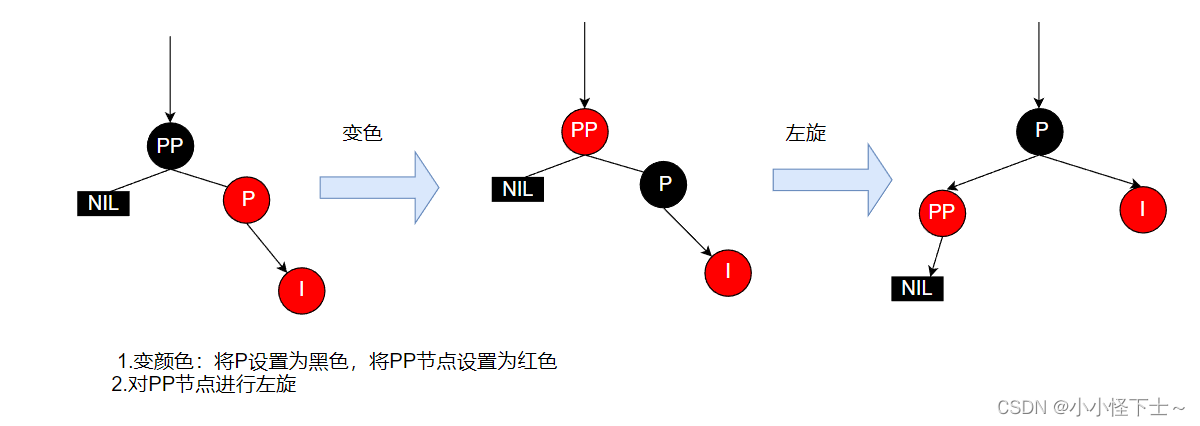
部分伪代码：
//1.得到通过插入节点得到爸爸节点 P 和 爷爷节点 PP,即插入节点为node RBNode P = parentOf(node); //parentOf()方法，通过此方法得到node的爸爸节点 RBNode PP = parentOf(parent); //2.变色 P.setColor(Black); PP.setColor(Red); //3.左旋 PP.right = P.left; //更新爷爷节点PP的右指向 if(P.left != null){ P.left.parent = PP; //更新爸爸节点的左子节点的父亲指向 } if(PP.parent != null){ //如果此时的PP.parent不为null，那么就说明此时的这个PP节点之下的树，只是一个子树而已 P.parent = PP.parent; //把爷爷节点原来的父亲之前赋给爸爸节点 if(PP.parent.left == PP){ PP.parent.left = P; }else if(PP.parent.right == PP){ PP.parent.right = P; } }else{ //此时的PP就是一棵树的根节点，于是直接调整根节点 this.root = P; this.root.parent = null; } //更新爷爷节点PP的指向,和爸爸节点P的指向 P.left = PP; PP.parent = P;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
情况4.3.2：
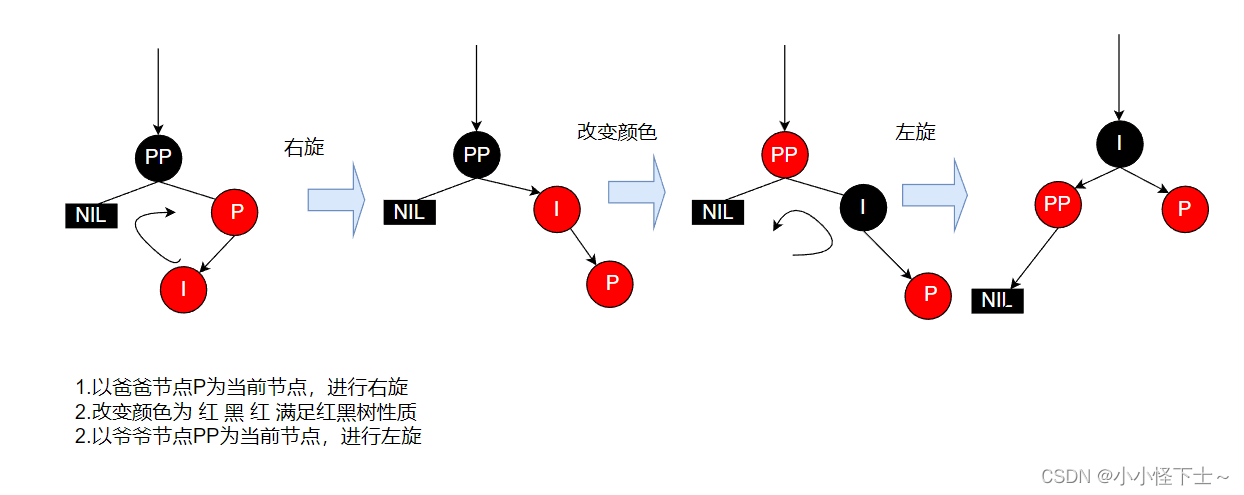
部分代码：
//右旋 // p p // | | // y x // / \ / \ // x ry lx y // / \ /\ //lx ly ly ry private void rightRotate(RBNode y){ RBNode x = y.left; y.left = x.right; if(x.right != null){ x.right.parent = y; } if(y.parent != null){ x.parent = y.parent; if(y.parent.left == y){ y.parent.left = x; }else{ y.parent.right = x; } }else{ this.root = x; this.root.parent = null; } y.parent = x; x.right = y; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
3. 手撕红黑树
public class RBTree<K extends Comparable<K>,V> { //设置红黑节点 private static final boolean RED = true; private static final boolean BLACK = false; //表示树跟 private RBNode root; public RBNode getRoot() { return root; } public void setRoot(RBNode root) { this.root = root; } /***获取当前节点的父亲节点**/ private RBNode parentOf(RBNode node){ if(node != null){ return node.parent; } return null; } /** 判断当前节点是不是红色**/ private boolean isRed(RBNode node){ if(node != null){ return node.color == RED; } return false; } /** 判断当前节点是不是黑色**/ private boolean isBlack(RBNode node){ if(node != null){ return node.color == BLACK; } return false; } /**设置节点红色**/ private void setRed(RBNode node){ if(node != null){ node.color = RED; } } /**设置节点红色**/ private void setBlack(RBNode node){ if(node != null){ node.color = BLACK; } } //中序遍历二叉树 public void inOrderPrint(){ this.inOrderPrint(root); } //中序打印 private void inOrderPrint(RBNode node){ if(node != null){ inOrderPrint(node.left); System.out.println("key : " + node.key + " " + "value = " + node.value); inOrderPrint(node.right); } } //左旋 // p p // | | // x y // / \ / \ // lx y x ry // / \ / \ // ly ry lx ly private void leftRotate(RBNode x){ RBNode y = x.right; x.right = y.left; if(y.left != null){ y.left.parent = x; } //此时的这个x作为头节点的一个树，其实是一棵子树 if(x.parent != null){ y.parent = x.parent; if(x == x.parent.left){ x.parent.left = y; }else{ x.parent.right = y; } }else{ //原来的x为根节点，那么就那y设置为root this.root = y; this.root.parent = null; } x.parent = y; y.left = x; } //右旋 // p p // | | // y x // / \ / \ // x ry lx y // / \ /\ //lx ly ly ry private void rightRotate(RBNode y){ RBNode x = y.left; y.left = x.right; if(x.right != null){ x.right.parent = y; } if(y.parent != null){ x.parent = y.parent; if(y.parent.left == y){ y.parent.left = x; }else{ y.parent.right = x; } }else{ this.root = x; this.root.parent = null; } y.parent = x; x.right = y; } //插入方法 public void insert(K key,V value){ RBNode node = new RBNode(); node.setKey(key); node.setValue(value); node.setColor(RED); insert(node); } private void insert(RBNode node){ //找到插入位置，插入节点 //设置父亲节点 RBNode parent = null; RBNode x = this.root; while(x != null){ parent = x; int cmp = node.key.compareTo(x.key); if(cmp > 0){ x = x.right; }else if(cmp == 0){ x.setValue(node.getValue()); return; }else{ x = x.left; } } node.parent = parent; if(parent != null){ //判断node和parent中的key谁大 int cmp = node.key.compareTo(parent.key); if(cmp > 0){ //当前node中的key比parent中的key大 parent.right = node; }else{ parent.left = node; } }else{ //第一次插入 this.root = node; } //自平衡 insertFixup(node); } private void insertFixup(RBNode node) { this.root.setColor(BLACK); //设置根节点为黑色 RBNode parent = parentOf(node); RBNode gparent = parentOf(parent); //情景1：插入的节点的父节点为红色 if(isRed(parent)){ //如果父节点是红色，那么就一定存在爷爷节点，因为在红黑树中的根节点不可能为红色节点 RBNode uncle = null; if(parent == gparent.left){ uncle = gparent.right; //uncle 存在 并且爸爸节点和叔叔节点都为红色，那么就把爸爸和叔叔节点的颜色变为黑色，爷爷节点的颜色变为红色 if(isRed(uncle)){ setBlack(parent); setBlack(uncle); setRed(gparent); //如果此时修改颜色之后，对其他节点产生了影响，并且此时还是不满足红黑树的性质，就继续在红黑树上向上判断，自平衡 insertFixup(gparent); return; } //4.2.1 uncle 不存在 或者为black if(uncle == null || isBlack(uncle)){ if(node == parent.left){ // 黑 红 黑 // / \ / \ / \ // 红 null / 黑 黑 null / 黑 红 红 // / / \ // 红 红 null / 黑 setBlack(parent); setRed(gparent); //右旋 rightRotate(gparent); //return; }else{ // 黑 黑 红 黑 // / \ / \ / \ / \ // 红 null / 黑 红 null / 黑 黑 null / 黑 红 红 // \ / / \ // 红 红 红 null/黑 leftRotate(parent); insertFixup(parent); return; } } }else{ uncle = gparent.left; if(isRed(uncle)){ setBlack(parent); setBlack(uncle); setRed(gparent); insertFixup(gparent); return; } if(uncle == null || isBlack(uncle)){ if(node == parent.getRight()){ // 黑 红 黑 // / \ / \ / \ // null/黑 红 null/黑 黑 红 红 // \ \ / // 红 红 null/黑 setBlack(parent); setBlack(uncle); setRed(gparent); leftRotate(gparent); return; }{ // 黑 黑 红 黑 // / \ / \ / \ / \ // null/黑 红 null/黑 红 null/黑 黑 红 红 // / \ \ / // 红 红 红 null/黑 rightRotate(parent); insertFixup(parent); return; } } } } } //定义节点中的属性 static class RBNode <K extends Comparable<K>,V>{ private RBNode parent; private RBNode left; private RBNode right; private boolean color; private K key; private V value; public RBNode(RBNode parent, RBNode left, RBNode right, boolean color, K key, V value) { this.parent = parent; this.left = left; this.right = right; this.color = color; this.key = key; this.value = value; } public RBNode(){ } public RBNode getParent() { return parent; } public void setParent(RBNode parent) { this.parent = parent; } public RBNode getLeft() { return left; } public void setLeft(RBNode left) { this.left = left; } public RBNode getRight() { return right; } public void setRight(RBNode right) { this.right = right; } public boolean isColor() { return color; } public void setColor(boolean color) { this.color = color; } public K getKey() { return key; } public void setKey(K key) { this.key = key; } public V getValue() { return value; } public void setValue(V value) { this.value = value; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
打印红黑树：
public class TreeOperation { /* 树的结构示例： 1 / \ 2 3 / \ / \ 4 5 6 7 */ // 用于获得树的层数 public static int getTreeDepth(RBTree.RBNode root) { return root == null ? 0 : (1 + Math.max(getTreeDepth(root.getLeft()), getTreeDepth(root.getRight()))); } private static void writeArray(RBTree.RBNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) { // 保证输入的树不为空 if (currNode == null) return; // 先将当前节点保存到二维数组中 res[rowIndex][columnIndex] = String.valueOf(currNode.getKey() + "-" + (currNode.isColor() ? "R" : "B") + ""); // 计算当前位于树的第几层 int currLevel = ((rowIndex + 1) / 2); // 若到了最后一层，则返回 if (currLevel == treeDepth) return; // 计算当前行到下一行，每个元素之间的间隔（下一行的列索引与当前元素的列索引之间的间隔） int gap = treeDepth - currLevel - 1; // 对左儿子进行判断，若有左儿子，则记录相应的"/"与左儿子的值 if (currNode.getLeft() != null) { res[rowIndex + 1][columnIndex - gap] = "/"; writeArray(currNode.getLeft(), rowIndex + 2, columnIndex - gap * 2, res, treeDepth); } // 对右儿子进行判断，若有右儿子，则记录相应的"\"与右儿子的值 if (currNode.getRight() != null) { res[rowIndex + 1][columnIndex + gap] = "\\"; writeArray(currNode.getRight(), rowIndex + 2, columnIndex + gap * 2, res, treeDepth); } } public static void show(RBTree.RBNode root) { if (root == null) System.out.println("EMPTY!"); // 得到树的深度 int treeDepth = getTreeDepth(root); // 最后一行的宽度为2的（n - 1）次方乘3，再加1 // 作为整个二维数组的宽度 int arrayHeight = treeDepth * 2 - 1; int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1; // 用一个字符串数组来存储每个位置应显示的元素 String[][] res = new String[arrayHeight][arrayWidth]; // 对数组进行初始化，默认为一个空格 for (int i = 0; i < arrayHeight; i ++) { for (int j = 0; j < arrayWidth; j ++) { res[i][j] = " "; } } // 从根节点开始，递归处理整个树 // res[0][(arrayWidth + 1)/ 2] = (char)(root.val + '0'); writeArray(root, 0, arrayWidth/ 2, res, treeDepth); // 此时，已经将所有需要显示的元素储存到了二维数组中，将其拼接并打印即可 for (String[] line: res) { StringBuilder sb = new StringBuilder(); for (int i = 0; i < line.length; i ++) { sb.append(line[i]); if (line[i].length() > 1 && i <= line.length - 1) { i += line[i].length() > 4 ? 2: line[i].length() - 1; } } System.out.println(sb.toString()); } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
测试类：
import java.util.Scanner; public class TestDemo { public static void main(String[] args) { RBTree<String,Object> rbTree = new RBTree<>(); Scanner scanner = new Scanner(System.in); while(true){ System.out.println("请输入key "); String key = scanner.next(); System.out.println(); rbTree.insert(key,null); TreeOperation.show(rbTree.getRoot()); } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
运行结果：
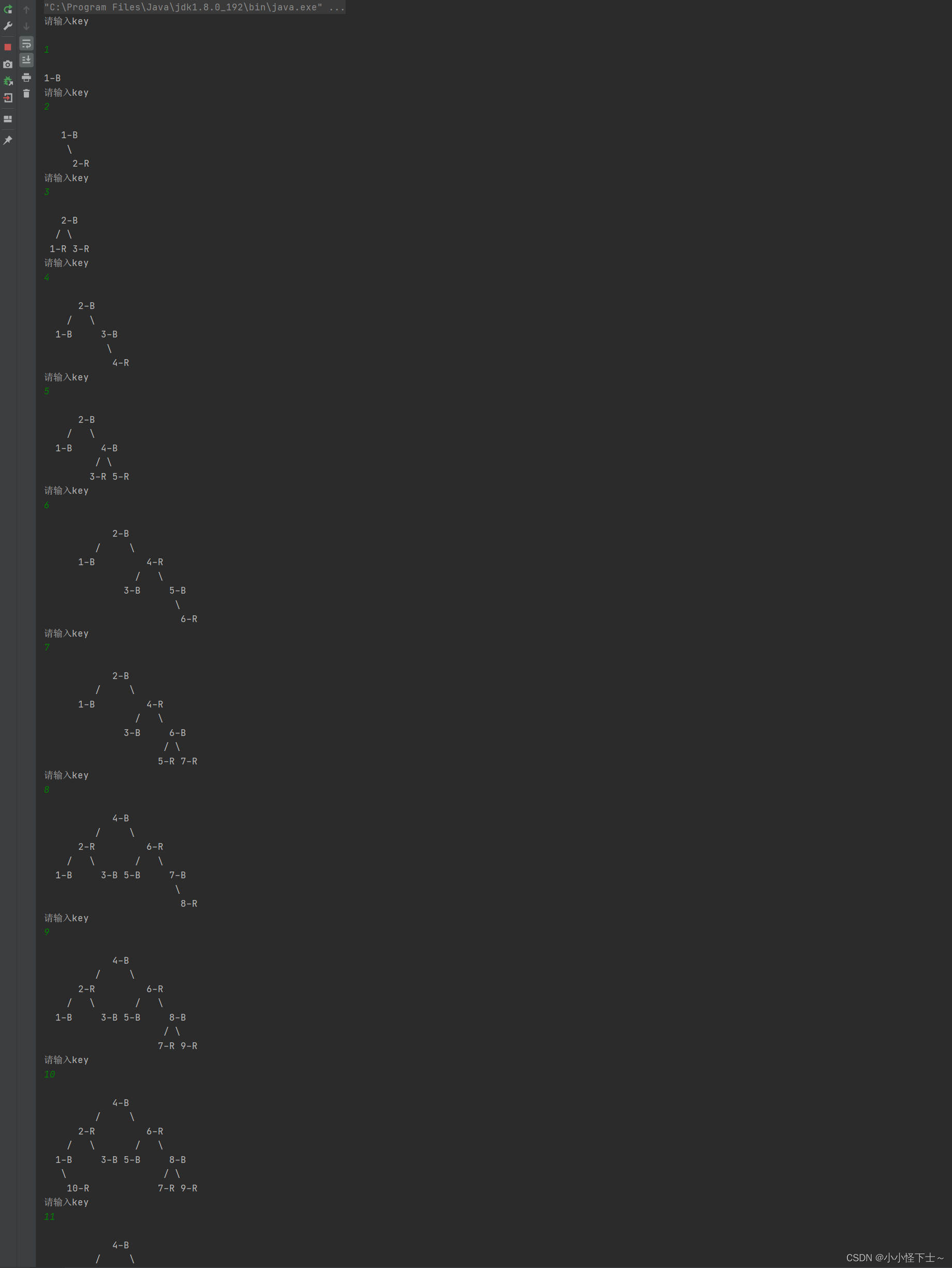
4. 通过总体聊聊AVL树和红黑树
AVL 的操作代价分析：
(1) 查找代价： AVL是严格平衡的BST（平衡因子不超过1）。那么查找过程与BST一样，只是AVL不会出现最差情况的BST(单支树)。因此查找效率最好，最坏情况都是O(logN)数量级的。
(2) 插入代价： AVL必须要保证严格平衡(|bf|<=1)，那么每一次插入数据使得AVL中某些结点的平衡因子超过1就必须进行旋转操作。事实上，AVL的每一次插入结点操作最多只需要旋转1次(单旋转或双旋转)。因此，总体上插入操作的代价仍然在O(logN)级别上(插入结点需要首先查找插入的位置)。
(3) 删除代价：AVL删除结点的算法可以参见BST的删除结点，但是删除之后必须检查从删除结点开始到根结点路径上的所有结点的平衡因子。因此删除的代价稍微要大一些。每一次删除操作最多需要O(logN)次旋转。因此，删除操作的时间复杂度为O(logN)+O(logN)=O(2logN)
AVL 效率总结 : 查找的时间复杂度维持在O(logN)，不会出现最差情况
AVL树在执行每个插入操作时最多需要1次旋转，其时间复杂度在O(logN)左右。
AVL树在执行删除时代价稍大，执行每个删除操作的时间复杂度需要O(2logN)。
红黑树(Red-Black Tree )
二叉平衡树的严格平衡策略以牺牲建立查找结构(插入，删除操作)的代价，换来了稳定的O(logN) 的查找时间复杂度。 红黑树并不追求“完全平衡”——它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。
RBT 的操作代价分析：
(1) 查找代价：由于红黑树的性质(最长路径长度不超过最短路径长度的2倍)，可以说明红黑树虽然不像AVL一样是严格平衡的，但平衡性能还是要比BST要好。其查找代价基本维持在O(logN)左右，但在最差情况下(最长路径是最短路径的2倍少1)，比AVL要略逊色一点。
(2) 插入代价：RBT插入结点时，需要旋转操作和变色操作。但由于只需要保证RBT基本平衡就可以了。因此插入结点最多只需要2次旋转，这一点和AVL的插入操作一样。虽然变色操作需要O(logN)，但是变色操作十分简单，代价很小。
(3) 删除代价：RBT的删除操作代价要比AVL要好的多，删除一个结点最多只需要3次旋转操作。
RBT 效率总结 : 查找 效率最好情况下时间复杂度为O(logN)，但在最坏情况下比AVL要差一些，但也远远好于BST。
插入和删除操作改变树的平衡性的概率要远远小于AVL（RBT不是高度平衡的）。因此需要的旋转操作的可能性要小，而且一旦需要旋转，插入一个结点最多只需要旋转2次，删除最多只需要旋转3次(小于AVL的删除操作所需要的旋转次数)。虽然变色操作的时间复杂度在O(logN)，但是实际上，这种操作由于简单所需要的代价很小。
AVL 和RBT 都是二叉查找树的优化。其性能要远远好于二叉查找树。他们之间都有自己的优势，其应用上也有不同。
结构对比： AVL的结构高度平衡，RBT的结构基本平衡。平衡度AVL > RBT.
查找对比： AVL 查找时间复杂度最好，最坏情况都是O(logN)。
RBT 查找时间复杂度最好为O(logN)，最坏情况下比AVL略差。
插入删除对比：
1. AVL的插入和删除结点很容易造成树结构的不平衡，而RBT的平衡度要求较低。因此在大量数据插入的情况下，RBT需要通过旋转变色操作来重新达到平衡的频度要小于AVL。
- 如果需要平衡处理时，RBT比AVL多一种变色操作，而且变色的时间复杂度在O(logN)数量级上。但是由于操作简单，所以在实践中这种变色仍然是非常快速的。
3. 当插入一个结点都引起了树的不平衡，AVL和RBT都最多需要2次旋转操作。但删除一个结点引起不平衡后，AVL最多需要logN 次旋转操作，而RBT最多只需要3次。因此两者插入一个结点的代价差不多，但删除一个结点的代价RBT要低一些。
4. AVL和RBT的插入删除代价主要还是消耗在查找待操作的结点上。因此时间复杂度基本上都是与O(logN) 成正比的。
总体评价：大量数据实践证明，RBT的总体统计性能要好于平衡二叉树。
-
-
相关阅读:
《Oracle系列》Oracle 通过触发器记录一张表所有数据的增删改操作，然后插入到另外一张表中
pybind11:python联合c++编译
如何理解方正证券量化交易接口的优势？
从新手到熟练，怎么学好Zbrush？
解放双手，根据代码自动生成时序图，这款IDEA插件真香~
vue 中为什么需要虚拟DOM、VDOM 是如何生成的、VDOM 如何做 diff 的?
java基于ssm的房屋租赁出租管理系统
(CVPR-2019)选择性的内核网络
【云原生 | Docker 高级篇】10、Docker 资源配额
数据可视化之雷达图：自助数据集处理，完美演绎球员数据可视化
- 原文地址：https://blog.csdn.net/qq_54883034/article/details/127747234
