[时间序列预测]基于BP、RNN、LSTM、CNN-LSTM算法多特征（多影响因素）用电负荷预测[保姆级手把手教学]

系列文章目录

深度学习原理-----线性回归+梯度下降法
深度学习原理-----逻辑回归算法
深度学习原理-----全连接神经网络
深度学习原理-----卷积神经网络
深度学习原理-----循环神经网络（RNN、LSTM）
时间序列预测-----基于BP、LSTM、CNN-LSTM神经网络算法的单特征用电负荷预测
时间序列预测(多特征)-----基于BP、LSTM、CNN-LSTM神经网络算法的多特征用电负荷预测

---

系列教学视频

快速入门深度学习与实战
[手把手教学]基于BP神经网络单特征用电负荷预测
[手把手教学]基于RNN、LSTM神经网络单特征用电负荷预测
[手把手教学]基于CNN-LSTM神经网络单特征用电负荷预测
[多特征预测]基于BP神经网络多特征电力负荷预测
[多特征预测]基于RNN、LSTM多特征用电负荷预测
[多特征预测]基于CNN-LSTM网络多特征用电负荷预测

---

前言

  在时间序列预测任务中，一般根据输入分为两种类别的任务，第一种任务是单特征输入的任务，例如在对股票闭盘价格进行预测的时候，输入到神经网络的数据只有股票的闭盘价格，也就是利用闭盘价格来预测闭盘价格，此时的闭盘价格数据既是特征X也是标签Y；还有一种任务是多特征输入的任务，在这样的任务下，神经网络的输入特征就不是单一的特征了，而是多特征的，例如在股票预测这样的案例中预测股票的闭盘价格，可以输入股票的开盘价、最高价、最低价、闭盘价来预测闭盘价，在多特征输入的时间预测任务，数据的预处理可能稍微要比单特征输入任务要复杂一些。
  类比上述的股票闭盘价格的预测任务，在电力负荷预测任务中也是一样的，单特征输入电力负荷预测输入的是电力负荷值，利用电力负荷值来预测电力负荷值；多特征电力负荷预测就是本文接下来要讲解的项目，在本项目中输入的特征有温度、湿度、电价和负荷特征，利用上述的特征来进行电力负荷的预测，具体讲解了利用BP神经网络、RNN、LSTM神经网络、组合的CNN-LSTM神经网络进行多特征电力负荷的预测，并最后进行对比。

---

一、多影响因素电力负荷数据分析

1.1、数据展示

  关于多影响因素的电力负荷预测深度学习实验数据集如下所示：
  具体数据可以去如下课程所获取，里面有理论到实战的讲解。
  [多特征预测]基于BP神经网络多特征电力负荷预测
  [多特征预测]基于RNN、LSTM多特征用电负荷预测
  [多特征预测]基于CNN-LSTM网络多特征用电负荷预测

  从数据的截图可以看出，该数据含有，干球温度、露点温度、湿球温度、湿度、电价和用电负荷数据；其中该数据是2006年到2010年，一共有5年的数据量。其中数据的采样点为半个小时采样一次，一天一共有48个采样点，除了2008年数据有17568个采样外，2006年、2007年、2009、2010年都为17520个采样点，因此数据一共有87648个采样点。

1.2、电力负荷和影响因素对比

  从直观的角度来讲，天气因素和电价对用电量是有一定的关系的。因此将电力负荷和天气电价在一个图上绘制出；具体的图如下所示：

  通过分析可以发现，不管是干球温度、露点温度还是湿球温度，它们随着时间的变化，其变化的趋势是及其相似的，因此可以判断他们之间存在着很强的相关性。通过观察电力负荷波形和温度数据的波形，发现当温度越高或者越低的时候，正是电力负荷数据越大的时候，因此可以判定温度数据和电力负荷数据之间存在着很强的相关性，温度的大小对电力负荷数据的大小的影响是很大的。进而观察湿度数据和电价数据，相对于温度数据，湿度数据观察不出明显的规律特征和周期特性。而电价数据除了某些时间段有很大的价格变动以外，没有明显的波动。从图中不能很明显的观察出湿度和电价对用电负荷有着很明显的影响。

1.3、分析电力负荷中的规律

  如图为该数据2006年到2010年5年的每年的用电负荷曲线图。

  从图2-6可以看出，2006年至2010年这5年期间，每年的的用电负荷趋势是大致相同的，呈现一定的周期性特性；每年的用电高峰大致都是在12月至2月、6月至8月，这很明显是和季节相关的。
  为了对数据有个更加全面的了解和更深入的解析。选取每年4月份倒数第二周的周电力负荷数据。图所示，图中的电力负荷数据分别为2006年4月17日至23日、2007年4月16日至22日、2008年4月21日至27日、2009年4月20日至26日、2010年4月19日至25日一共5周的周电力负荷数据。

  从图中可以看出每年的4月份倒数第二周的周电力负荷数据的趋势是及其相似的，尤其周六和周日的数据是很吻合的。而2006年4月17日和2008年4月25日的用电负荷相对其他年份的用电数据来说出现了明显的降低，但是用电的趋势是相似的。导致该曲线特性的原理可能是由于电力数据是有一定的随机性和外部的多种影响因素相关，不同年份的同一月的同一个星期的用电负荷曲线可能因为当时天气的异常、停电等一系列的外部原因导致有一定的差异。虽然不同的年份的周电力负荷数据有一定的差异，但是从中也可以得出共有的规律；不管是哪个年份，一周的数据呈现很明显的周期性变化，一周的波形近似于正弦波，这很显然和人们的生活作息是相关的，人们在夜间休息的时候用电量急剧下滑，导致用电在夜间处于一个很低的数值，而在白天要维持工作和生活又要消耗大量的电力能源，因此电力的消耗随着人们的休息完毕呈现一个急剧上升的一个状态；反反复复呈现一个周期循环的一个状态。
  从上述的分析可以得出一个基本的的结论，天气影响因素对用电量是用一定的影响因素的，同时电力负荷数据又是一个典型的时间序列数据，因为数据不断呈现周期性的变化，该变化和人们的生活作息有着很强的相关性；因此前面时刻的用电数据对后续用电是有着一定的影响的，这是时间序列数据典型的特征。
  本文的多特征电力负荷预测实验数据是半个小时一个采样点，也就是一天将会采样48个点。由于前面分析过电力负荷数据是随着人的作息而成周期性变化的，同时还有天气和电价等因素对其产生影响；因而在多特征电力负荷预测中取前面48个采样点中的天气因素、电价、负荷数据作为模型的输入特征来预测第49个采样点的电力负荷数据；以此为规律不断的滚动下去。

---

二、基于BP神经网络多特征电力负荷预测

2.1、BP神经网络模型应用于多特征电力负荷预测

  现在回到多特征电力负荷预测任务上来，从任务的本质上来说，多特征电力负荷预测本质上还是一个回归预测任务，只不过在神经网络输入上相对于单特征电力负荷来说，输出中多了天气影响因素、电价影响因素；就神经网络搭建来说，网络的搭建变化不大，同时在现在深度学习框架发展成熟的情况下，搭建网络就变成一个很简单的事情了；但是相对于单特征电力负荷预测，数据处理，构建成BP神经网络可以学习的数据格式要稍稍复杂一点。
  我一直认为对于初学者来说，利用深度学习来训练一个自己任务的网络模型有两点比较复杂；第一点就是环境的搭建、第二点就是数据处理，因此在我的课程中有很详细的手把手教学，大家可以看看。
  [多特征预测]基于BP神经网络多特征电力负荷预测
  [多特征预测]基于RNN、LSTM多特征用电负荷预测
  [多特征预测]基于CNN-LSTM网络多特征用电负荷预测
  下面我们整体看看BP神经网络怎么利用多特征电力负荷数据进行电力负荷预测任务的。和前面单特征电力负荷预测一样，BP神经网络模型的结构如下所示：

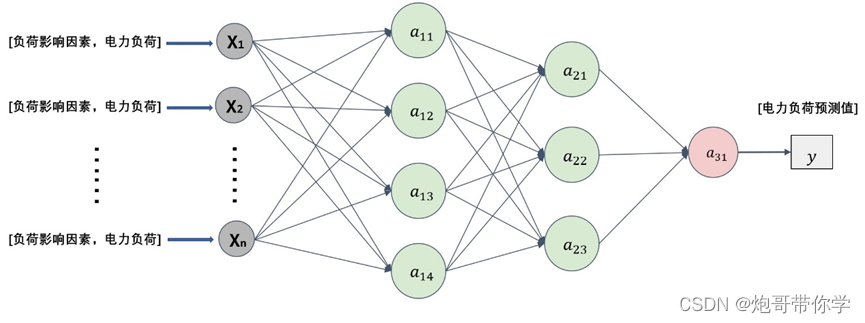
  从上面的图分析可以发现，相对于单特征负荷预测模型来说，他们之间唯一的不同就是，输入数据的不同，单特征的输入数据只有前面采样点的电力负荷数据，而多特征电力负荷预测的输入数据为前面采样点中含有对电力负荷影响因素和电力负荷数据；他们最终的预测值为电力负荷值；因此这两个模型在电力负荷数据处理上有着显然的不同，这也是电力负荷预测模型的难点之一。

2.2、 数据预处理与数据集划分

  如下是电力负荷预测数据集的预处理与划分部分：

# 进行数据归一化，将数据归一化到0-1之间
scaler = MinMaxScaler(feature_range=(0, 1))
train = scaler.fit_transform(train)
val = scaler.fit_transform(val)

"""
进行训练集数据特征和对应标签的划分，其中前面48个采样点中的天气特征、电价特征和负荷特征
来预测第49个点的电力负荷值。
"""

# 设置训练集的特征列表和对应标签列表
x_train = []
y_train = []

for i in np.arange(48, len(train)):
    x_train.append(train[i - 48:i, :])
    y_train.append(train[i, 5])
    
# 将训练集由list格式变为array格式
x_train, y_train = np.array(x_train), np.array(y_train)
x_train, y_train = np.reshape(x_train, (x_train.shape[0], 48*6)), np.reshape(y_train, (y_train.shape[0], 1))

# 设置训练集的特征列表和对应标签列表
x_val = []
y_val = []

for i in np.arange(48, len(val)):
    x_val.append(val[i - 48:i, :])
    y_val.append(val[i, 5])

# 将训练集由list格式变为array格式
x_val, y_val = np.array(x_val), np.array(y_val)
x_val, y_val = np.reshape(x_val, (x_val.shape[0], 48*6)), np.reshape(y_val, (y_val.shape[0], 1))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

  首先对获取的数据进行归一化的处理，在电力负荷数据中不同特征之间的物理量纲是不一样的，那么就可能到导致有些物理量的数值比较大，在神经网络计算的时候会使其误认为该特征比较重要，同时也会使时间网络的计算比较慢，因此在进行数据预测的时候第一步就是对其进行归一化预处理，将所有的特征归一化到0-1之间。
  同时设置训练集和验证集对应的特征和标签的列表用来装对应的数据和标签，方便后续神经网络可以利用数据特征进行学习，在利用前向传播输出值和真实标签计算出来的误差进行反向传播更新神经网络的权重参数，从而使神经网络从数据中不断学习到有用信息。

---

2.3、模型搭建

如下是利用深度学习框架搭建的BP神经网络模型：

# 利用keras搭建BP神经网络，该网络隐藏层一共有两层，神经元分别为10
model = Sequential()
model.add(Dense(10, activation='relu'))
model.add(Dense(10, activation='relu'))
model.add(Dense(1))


# 对模型进行编译，选用Adam优化器，学习率为0.01
model.compile(optimizer=keras.optimizers.Adam(0.01), loss='mean_squared_error')

# 将训练集和测试集放入网络进行训练，每批次送入的数据为512个数据，一共训练30轮，将测试集样本放入到神经网络中测试其验证集的loss值
history = model.fit(x_train, y_train, batch_size=512, epochs=30, validation_data=(x_val, y_val))

# 保存训练好的模型
model.save('BP_model.h5')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

  此时BP神经网络已经搭建完毕，此时可以进行神经网络的训练了，同时将训练好的网络模型保存到BP_model.h5中，后续可以该训练好的模型参数进行电力负荷的预测推理了。
  如下图为BP电力负荷网络训练的过程：
  从下图图可以看到神经网络的训练集和验证集的loss在不断的下降，很显然神经网络模型在不断的收敛。具体看一下BP神经网络的最终的loss值对比图如下所示：

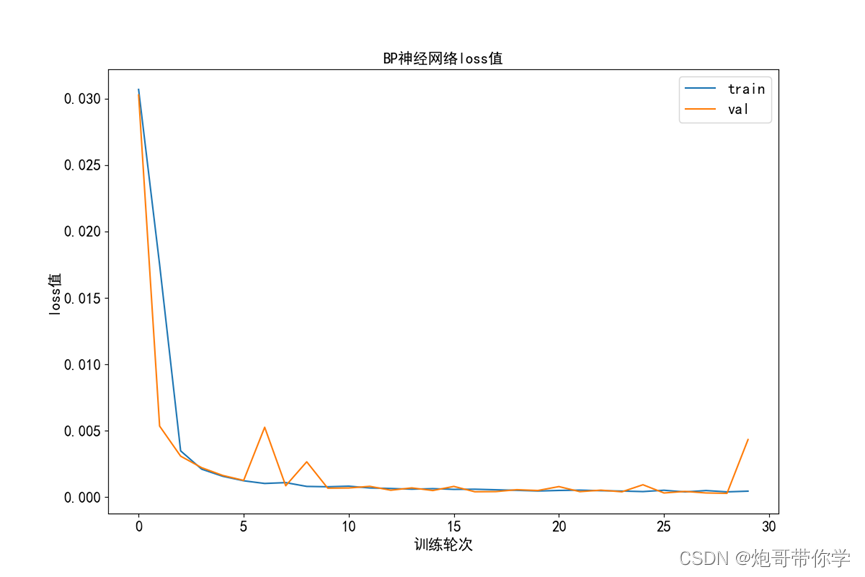
  如上图所示，该图记录了BP神经网络30轮训练过程中的训练集和验证集的loss值，很显然在15轮以后该神经网络模型就已经收敛。

---

2.4、模型预测

  从项目文件夹中可以看到已经产生保存训练好的模型文件，利用该模型参数文件可以直接对输入数据特征进行模型推理，产生的模型文件如下图所示:

  此时可以利用训练好的模型对测试进行测试，并对预测出来的预测值进行反归一化处理。具体代码如下所示：

# 导入训练好的模型权重文件
model = load_model("BP_model.h5")


# 测试集输入模型进行预测
predicted = model.predict(x_test)
# print(predicted.shape)
# print(test.shape)

# 将真实值标签进行反归一化操作，方便后续和真实值进行对比
real = np.concatenate((test[48:, :-1], y_test), axis=1)
real = scaler.inverse_transform(real)
real = real[:, 5]


# 将模型预测出的值进行反归一化操作
prediction = np.concatenate((test[48:, :-1], predicted), axis=1)
prediction = scaler.inverse_transform(prediction)
prediction = prediction[:, 5]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

  将预测值和真实的标签进行对比，并绘制如下的预测值和真实值的对比图。

  从上图对比可以发现，BP神经网络对电力负荷预测是有一定的效果的，但是可以看出在峰值和峰谷的预测和真实值是有一定的误差的。具体可以利用模型的评价指标对模型进行评价。

# 计算模型的评价指标
R2 = r2_score(real, prediction)
MAE = mean_absolute_error(real, prediction)
RMSE = np.sqrt(mean_squared_error(real, prediction))
MAPE = np.mean(np.abs((real-prediction) / prediction))

# 打印模型的评价指标
print('R2:', R2)
print('MAE:', MAE)
print('RMSE:', RMSE)
print('MAPE:', MAPE)
1
2
3
4
5
6
7
8
9
10
11
12

  具体的评价指标计算如下

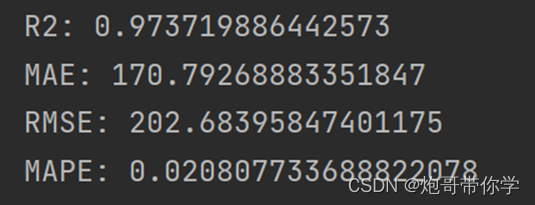
  更加详细的讲解和完整代码可以去我的课程去获取：
  [多特征预测]基于BP神经网络多特征电力负荷预测
  [多特征预测]基于RNN、LSTM多特征用电负荷预测
  [多特征预测]基于CNN-LSTM网络多特征用电负荷预测

---

三、基于RNN、LSTM神经网络多特征电力负荷预测

3.1、RNN、LSTM神经网络模型应用于多特征电力负荷预测

  在前面的文章中已经很详细的讲解了RNN/LSTM神经网络模型的原理了有不懂的可以具体看看这篇文章深度学习原理-----循环神经网络（RNN、LSTM），同时也可以去看看我录制的课程，里面很详细的对这个模型进行了讲解快速入门深度学习与实战。
  现在我们已经知道了RNN神经网络的模型和LSTM神经网络的模型可以用如下的图表示：

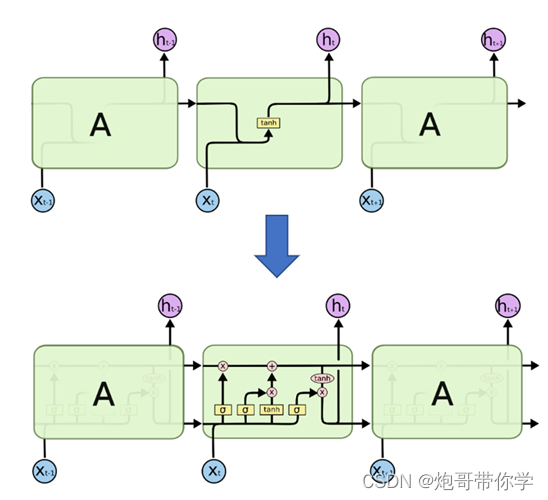
  如上图所示，该图为RNN神经网络和LSTM神经网络的对比图，其中上面的图为RNN神经网络的结构图，下面的图为LSTM神经网络的结构图，很显然除了神经网络单元不一样以外，RNN神经网络和LSTM神经网络基本是一样的。那么下面就以LSTM神经网络为例来看看LSTM神经网络怎么利用多特征电力负荷数据进行电力负荷预测任务的。

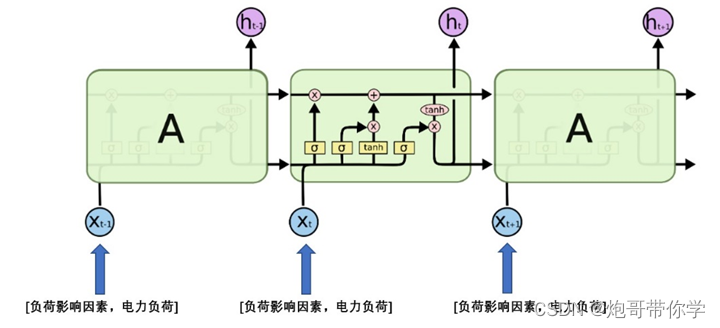
  如上图所示，展示了多特征电力负荷数据如何输入到LSTM神经网络中；这里要强调一点，看这个图不能从整体上看，而是应该从左往右看，也就是有先后顺序的。图中绘制了3个时间步的数据输入。首先输入t-1时刻的负荷影响因素和电力负荷数据值进行LSTM神经网络单元的计算，计算出来值分别送到两个地方，第一个作为该神经网络隐层的输出输出到下一层去，第二个作为下一个时间步的输入；因此在t时间输入的数据为该时刻的负荷影响因素和电力负荷数据同时还有上一时刻时间步的输出结果，因此t的时刻的输入包好前面时刻的信息。t时刻的输出和t-1时刻一样有两个输出。而t+1时刻的计算和t时刻的计算是一样的，因此按照上述的规律不断的计算直至设置的最后的一个时刻计算结束。
  本文的数据是半个小时一个采样点，也就是一天将会采样48个点。由于前面分析过电力负荷数据是随着人的作息而成周期性变化的，同时还有天气和电价等因素对其产生影响；因而在多特征电力负荷预测中取前面48个采样点中的天气因素、电价、负荷数据作为模型的输入特征来预测第49个采样点的电力负荷数据；以此为规律不断的滚动下去。
  因此在此实验中，LSTM神经网络要不断循环计算48个时间步直至最终的预测值输出。这里要强调一下，计算48个时间步不是说上述的计算单元有48个，而是同样的一个单元不断重复计算48次，因此这样的神经网络又叫作循环神经网络。同理RNN神经网络和LSTM神经网络的计算过程是一样的。

---

3.2、数据预处理与数据集划分

  如下是电力负荷预测数据集的预处理与划分部分：

# 进行数据归一化，将数据归一化到0-1之间
scaler = MinMaxScaler(feature_range=(0, 1))
train = scaler.fit_transform(train)
val = scaler.fit_transform(val)
"""
进行训练集数据特征和对应标签的划分，其中前面48个采样点中的天气特征、电价特征和负荷特征
来预测第49个点的电力负荷值。
"""
# 设置训练集的特征列表和对应标签列表
x_train = []
y_train = []

# 将前48个采样点的天气特征和电价特征和负荷特征作为训练特征添加到列表中
# 按照上述规律不断滑动取值
for i in np.arange(48, len(train)):
    x_train.append(train[i - 48:i, :])
    y_train.append(train[i, 5])

# 将训练集由list格式变为array格式,LSTM神经网络的输入格式3维，样式为（输入样本数，时间步，特征数量）
x_train, y_train = np.array(x_train), np.array(y_train)

# 设置训练集的特征列表和对应标签列表
x_val = []
y_val = []

# 将前48个采样点的天气特征和电价特征和负荷特征作为训练特征添加到列表中
# 按照上述规律不断滑动取值
for i in np.arange(48, len(val)):
    x_val.append(val[i - 48:i, :])
    y_val.append(val[i, 5])

# 将训练集由list格式变为array格式
x_val, y_val = np.array(x_val), np.array(y_val)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

  如上是LSTM神经网络模型的数据预处理和训练集和验证集的划分部分，和前面的BP神经网络数据集的预处理一样，数据在拿到手后一定要进行数据的归一化处理，这一步加速了神经网络的参数更新的同时也有利于提高神经网络的预测精度。
  这里要强调一下，RNN和LSTM等循环神经网络输出网络模型的数据的格式是[样本数，时间步，特征数量]；样本数量很好理解，就是训练集一共有多少样本；时间步就是循环神经网络一共要循环多少次计算，例如本案例的实验是利用前面48个时间步的影响因素和负荷数据作为特征来预测第49个点的数据，那么循环神经网络就需要循环计算48次，每次计算一个时间步的特征数据；特征数据也很好理解，在本实验中就是影响因素加上负荷，具体为干球温度、露点温度、湿球温度、湿度、电价和用电负荷数据这6个特征（这里需要注意的是电力负荷数据既是特征又是标签）。因此我们来看看最终制作的数据集的数据维度为：

  显然训练集的样本有67600个，时间步为48，特征为6；显然验证集的样本有9952个，时间步为48，特征为6。

3.3、模型搭建

  如下是利用深度学习框架搭建的RNN神经网络模型：

# 利用keras搭建RNN神经网络，该网络隐藏层一共有两层，神经元分别为10
model = Sequential()
model.add(SimpleRNN(10, return_sequences=True, activation='relu'))
model.add(SimpleRNN(10, return_sequences=False, activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(1))

# 对模型进行编译，选用Adam优化器，学习率为0.01
model.compile(optimizer=keras.optimizers.Adam(0.01), loss='mean_squared_error')

# 将训练集和测试集放入网络进行训练，每批次送入的数据为512个数据，一共训练30轮，将测试集样本放入到神经网络中测试其验证集的loss值
history = model.fit(x_train, y_train, batch_size=512, epochs=30, validation_data=(x_val, y_val))

# 保存训练好的模型
model.save('RNN_model.h5')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

如下是利用深度学习框架搭建的LSTM神经网络模型：

# 利用keras搭建LSTM神经网络，该网络隐藏层一共有两层，神经元分别为10
model = Sequential()
model.add(LSTM(10, return_sequences=True, activation='relu'))
model.add(LSTM(10, return_sequences=False, activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(1))

# 对模型进行编译，选用Adam优化器，学习率为0.01
model.compile(optimizer=keras.optimizers.Adam(0.01), loss='mean_squared_error')

# 将训练集和测试集放入网络进行训练，每批次送入的数据为512个数据，一共训练30轮，将测试集样本放入到神经网络中测试其验证集的loss值
history = model.fit(x_train, y_train, batch_size=512, epochs=30, validation_data=(x_val, y_val))

# 保存训练好的模型
model.save('LSTM_model.h5')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

  下面利用LSTM神经网络作为例子进行讲解。LSTM神经网络训练的过程如下图所示,可以看到loss值在不断的下降，模型训练完毕后，模型的loss值如下所示：

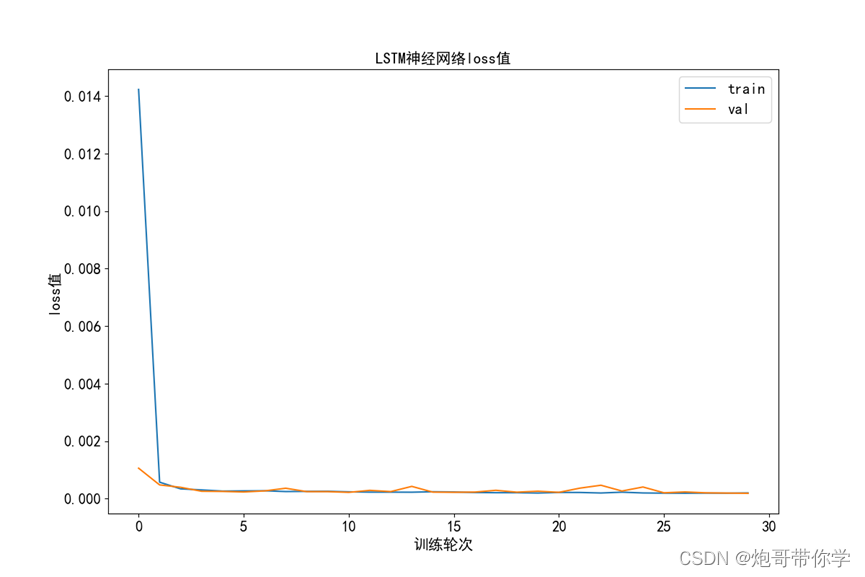
  很显然该网络在5轮左右的时候就已经接近收敛，相对于BP神经网络来说，收敛的更快。

---

3.4、模型预测

  模型训练完了以后保存训练好的模型，利用该模型参数文件可以直接对输入数据特征进行模型推理，产生的模型参数如下:

  此时可以利用训练好的模型对测试进行测试，并对预测出来的预测值进行反归一化处理。具体代码如下所示：

# 导入训练好的模型参数
model = load_model("LSTM_model.h5")


# 测试集输入模型进行预测
predicted = model.predict(x_test)


# 将真实值标签进行反归一化操作，方便后续和真实值进行对比
real = np.concatenate((test[48:, :-1], y_test), axis=1)
real = scaler.inverse_transform(real)
real = real[:, 5]

# 将模型预测出的值进行反归一化操作
prediction = np.concatenate((test[48:, :-1], predicted), axis=1)
prediction = scaler.inverse_transform(prediction)
prediction = prediction[:, 5]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

  将预测值和真实的标签进行对比，并绘制如下的预测值和真实值的对比图。

  从上图对比可以发现，LSTM神经网络对电力负荷预测的效果是很不错的，具体可以利用模型的评价指标对模型进行评价。
  具体的评价指标代码如下

# 计算模型的评价指标
R2 = r2_score(real, prediction)
MAE = mean_absolute_error(real, prediction)
RMSE = np.sqrt(mean_squared_error(real, prediction))
MAPE = np.mean(np.abs((real-prediction) / prediction))

# 打印模型的评价指标
print('R2:', R2)
print('MAE:', MAE)
print('RMSE:', RMSE)
print('MAPE:', MAPE)
1
2
3
4
5
6
7
8
9
10
11

  具体的评价指标计算如下：

  更加详细的讲解和完整代码可以去我的课程去获取：
  [多特征预测]基于BP神经网络多特征电力负荷预测
  [多特征预测]基于RNN、LSTM多特征用电负荷预测
  [多特征预测]基于CNN-LSTM网络多特征用电负荷预测

---

四、基于CNN-LSTM神经网络多特征电力负荷预测

  相比较单一的神经网络模型，在有些场景下往往组合模型的效果要优于单一模型的效果，因为组合模型往往存在着模型优势互补的情况。CNN-LSTM网络模型是该系列讲解的第一个组合神经网络模型。从神经网络模型的名字就不难发现，该神经网络模型是由CNN神经网络和LSTM神经网络进行组合对电力负荷数据进行学习预测的。但是这里要强调一下，这里使用的CNN神经网络是一维卷积神经网络；而大家在深度学习的学习过程中接触到的卷积神经网络基本上是2维卷积神经网络，因为相比较其他的神经网络而言，二维卷积神经网络在图像的特征提取上效果的确要优于其他的神经网络；但是本文是利用组合神经网络模型对电力负荷数据进行特征的提取，由上面的分析可以知道电力负荷数据是一个典型的时间序列模型的数据。因此可以利用一维卷积神经网络进行时间序列数据的提取。在学习一维卷积神经网络之前建议学习一下二维卷积神经网络，这里有我写的相关文章和对应的视频课程深度学习原理-----卷积神经网络 ，快速入门深度学习与实战。

4.1、一维卷积运算和池化运算

4.1.1、一维卷积运算

  相对于二维卷积运算在整个特征图上进行左右上下滑动进行卷积运算，一维卷积运算只在数据特征H上进行不断的滑动进行卷积运算。具体如图所示。

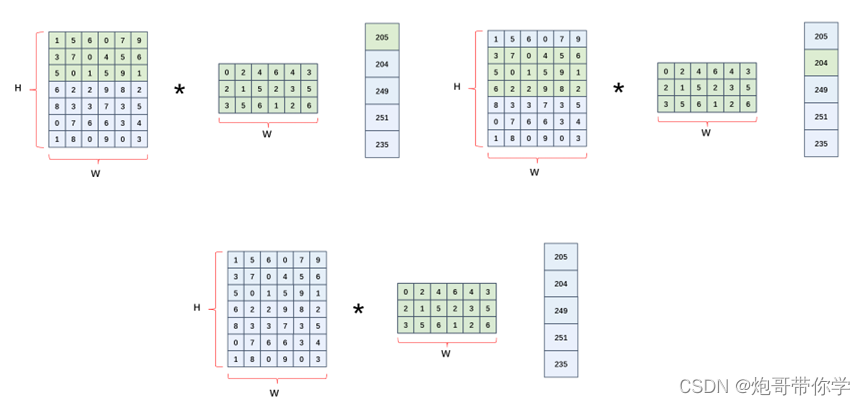
  如上图所示，假设此时的数据的维度为H×W，那么此时只要设定卷积核的高就行，如图所示，设卷积核的高为3，那么该卷积核的维度大小一定为3×W，因为一维卷积运算只进行一个方向的滑动；当然该卷积运算也可以在设定步幅等二维卷积运算有的操作。利用设定好的卷积核在数据特征上进行不断滑动，卷积核和对应的感受野进行对应因素相乘最后求和。不断重复操作直到不能再往下滑动为止。具体的操作如上图所示。
  当然进行一维卷积的数据不一定是单通道的数据，该数据可能有多个通道，同时希望人为设定经过卷积运算输出数据的通道，具体计算如下图所示：

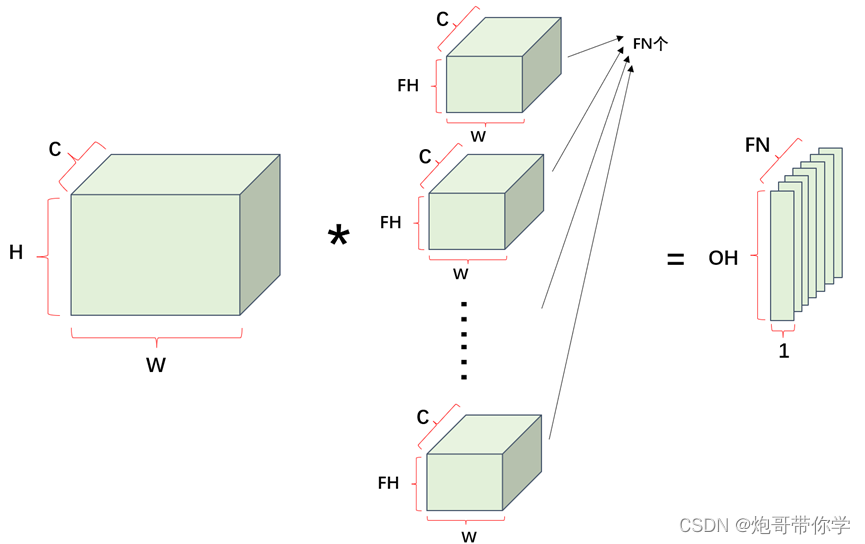
  如上图所示，假设输入数据的维度大小为H×W×C；那么此时对应的卷积核的通道数量一定为C，同时一维卷积运算的卷积核的宽一定要和特征图的宽一样，那么卷积核的宽也为W；同时设定卷积核的高为FH，那么卷积核的维度为FH×W×C；如果想设定输出数据的通道数量，那么就要设定卷积核的数量；假设希望输出的数据的通道大小为FN，那么就要设定卷积核的数量为FN个。因此通过计算最终输出的数据的维度为OH×1×FN。

4.1.2、一维池化运算

  和二维池化一样，一维卷积运算有最大池化和平均池化两种池化方式，下面来具体看看。
  （1）最大池化
  最大池化，就是对选定的区域选取最大值，具体和二维池化操作一样，具体如下图所示：

  （2）平均池化
  平均池化，就是对选定的区域选取平均值，具体和二维池化操作一样，具体如下图所示：

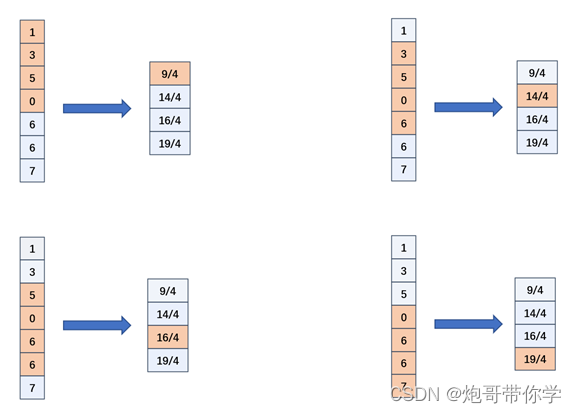
4.2、CNN-LSTM模型应用于多影响因素电力负荷预测

  经过如上的一维卷积运算和池化运行的分析以后搭建如下图所示的CNN-LSTM的组合神经网络模型。

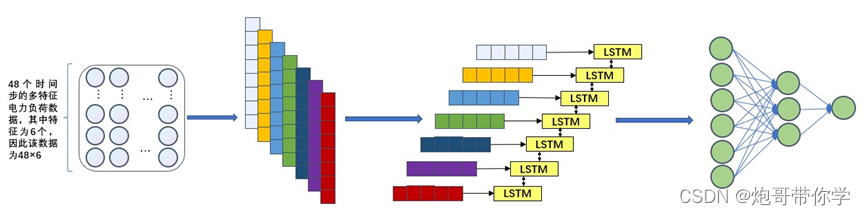
  由图可知，该神经网络的网络的输入是多特征的电力负荷数据，数据是30分钟以采样，那么就是一天的采样是48个时间点，电力负荷数据是典型的时间序列数据，前面的数据时间的数据对后面数据有着一定的影响，前面对该数据进行了分析，该份数据是以天为周期的数据，因此取48个点作为数据的输入，而数据的影响特征有为干球温度、露点温度、湿球温度、湿度、电价和用电负荷数据这6个特征，因此输入的数据为48×6这样的维度。
  首先对数据进行一维卷积运算，由前面可知一维卷积运算后的数据是一个N×1维度的数据，图中利用7个卷积核进行一维卷积算法，因此得出的7个N×1维的数据；也就是得到一个数据通道数为7，长和宽为N×1的数据。
  然后对卷积完的数据进行一维池化运算，不管是二维池化还是一维池化，进行池化运算后的数据通道数是不变的。经过一维池化运算后的数据的长比原来小了（当然也可能不变或者变大，具体要看池化运算的具体参数值）。经过池化运算后的数据也是可以再进行一维卷积运算的，但是为了方便观察整体的结构，本文的模型就画了一个卷积和一个池化运算。
  最后将经过卷积神经网络提取出来的特征结构输入到LSTM神经网络中，由LSTM神经网络对其进行时间序列信息的学习。并在神经网络结构最后接入全连接神经网络层，由全连接神经网络对前面提取和学习到特征进行预测，最终输出预测值。

4.3、数据预处理与数据集划分

  如下是电力负荷预测数据集的预处理与划分部分：

# 进行数据归一化，将数据归一化到0-1之间
scaler = MinMaxScaler(feature_range=(0, 1))
train = scaler.fit_transform(train)
val = scaler.fit_transform(val)

"""
进行训练集数据特征和对应标签的划分，其中前面48个采样点中的天气特征、电价特征和负荷特征
来预测第49个点的电力负荷值。
"""
# 设置训练集的特征列表和对应标签列表
x_train = []
y_train = []
# 将前48个采样点的天气特征和电价特征和负荷特征作为训练特征添加到列表中
# 按照上述规律不断滑动取值
for i in np.arange(48, len(train)):
    x_train.append(train[i - 48:i, :])
    y_train.append(train[i, 5])

# 将训练集由list格式变为array格式, LSTM神经网络的输入格式3维，样式为（输入样本数，时间步，特征数量）
x_train, y_train = np.array(x_train), np.array(y_train)

# 设置训练集的特征列表和对应标签列表
x_val = []
y_val = []

# 将前48个采样点的天气特征和电价特征和负荷特征作为训练特征添加到列表中
# 按照上述规律不断滑动取值
for i in np.arange(48, len(val)):
    x_val.append(val[i - 48:i, :])
    y_val.append(val[i, 5])

# 将训练集由list格式变为array格式
x_val, y_val = np.array(x_val), np.array(y_val)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

4.4、模型搭建

  如下是利用深度学习框架搭建的CNN-LSTM神经网络模型：

model = Sequential()
model.add(Conv1D(filters=32, kernel_size=3, strides=1, activation="relu"))
model.add(MaxPooling1D(pool_size=2, strides=1,))
model.add(Conv1D(filters=64, kernel_size=2, strides=1, activation="relu"))
model.add(MaxPooling1D(pool_size=3, strides=1))
model.add(LSTM(10, return_sequences=True, activation='relu'))
model.add(LSTM(10, return_sequences=False, activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(1))

# 对模型进行编译，选用Adam优化器，学习率为0.01
model.compile(optimizer=keras.optimizers.Adam(0.01), loss='mean_squared_error')

# 将训练集和测试集放入网络进行训练，每批次送入的数据为512个数据，一共训练30轮，将测试集样本放入到神经网络中测试其验证集的loss值
history = model.fit(x_train, y_train, batch_size=512, epochs=1, validation_data=(x_val, y_val))
# print(model.summary())

# 保存训练好的模型
model.save('CNN_LSTM_model.h5')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

  CNN-LSTM神经网络训练的过程如下图所示,可以看到loss值在不断的下降：

4.5、模型预测

  模型训练完了以后保存训练好的模型，利用该模型参数文件可以直接对输入数据特征进行模型推理，产生的模型参数如下:

  此时可以利用训练好的模型对测试集进行测试，并对预测出来的预测值进行反归一化处理。具体代码如下所示：

# 导入训练好的模型参数
model = load_model("CNN_LSTM_model.h5")


# 测试集输入模型进行预测
predicted = model.predict(x_test)


# 将真实值标签进行反归一化操作，方便后续和真实值进行对比
real = np.concatenate((test[48:, :-1], y_test), axis=1)
real = scaler.inverse_transform(real)
real = real[:, 5]

# 将模型预测出的值进行反归一化操作
prediction = np.concatenate((test[48:, :-1], predicted), axis=1)
prediction = scaler.inverse_transform(prediction)
prediction = prediction[:, 5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

  将预测值和真实的标签进行对比，并绘制如下的预测值和真实值的对比图。

  貌似CNN-LSTM神经网络的预测结果没有单一的LSTM神经网络结果预测效果好，具体看看模型的评价指标。
  具体的评价指标代码如下：

# 计算模型的评价指标
R2 = r2_score(real, prediction)
MAE = mean_absolute_error(real, prediction)
RMSE = np.sqrt(mean_squared_error(real, prediction))
MAPE = np.mean(np.abs((real-prediction) / prediction))

# 打印模型的评价指标
print('R2:', R2)
print('MAE:', MAE)
print('RMSE:', RMSE)
print('MAPE:', MAPE)
1
2
3
4
5
6
7
8
9
10
11

  具体的评价指标计算如下：

  更加详细的讲解和完整代码可以去我的课程去获取：
  [多特征预测]基于BP神经网络多特征电力负荷预测
  [多特征预测]基于RNN、LSTM多特征用电负荷预测
  [多特征预测]基于CNN-LSTM网络多特征用电负荷预测

---

五、多特征电力负荷预测模型对比分析总结

  我们已经搭建好BP、LSTM、CNN-LSTM神经网络，并利用测试集对其进行测试了，同时也计算出来对应模型的评价指标的指数，下面利用这样的评价指标的值对上述搭建的神经网络模型进行分析。具体的评价指标的值入下表所示：

  如上表所示，是本文利用BP、LSTM、CNN-LSTM神经网络对多特征电力负荷预测的评价指标；其中评价指标有R2、MAE、RMSE、MAPE；R2是值越接近1越好，而MAE、RMSE、MAPE三个评价指标是越接近0越好；从表中可以得出，LSTM效果最好、CNN-LSTM效果要次之、BP的效果最差，分析可得出如下的结论：
  1、本文的数据量比较充足，因此最终三个算法模型在效果上其实都是很不错的。可以很好的预测出电力负荷数值。
  2、从大量的论文来看，最终证明CNN-LSTM的效果是比LSTM效果好的，但是本文得出的效果是LSTM效果好，其中原因有如下可能：
（1）本文中的LSTM和CNN-LSTM的模型参数没有经过调参，因此不一定是最优模型。
（2）本文并没有在大量的实验下进行统计，只是做了一两次实验得出来的实验结果，可能具有偶然性。
（3）本文的数据是比较充足的，是否在数据比较少的情况下才可以显现出CNN-LSTM模型的优越性。

---

六、电力负荷预测模型后续更新计划

  以下的相关算法的电力负荷预测模型相关文章和教学视频预计在23年年底全部更新完毕，如果有想继续学习电力负荷预测，或者需要毕设的可以关注我，同时将该文章收藏，我会持续不断的更新相关的文章和教学视频。
   6.1、基于BP、LSTM、CNN-LSTM神经网络算法的单特征用电负荷预测（完结）
  6.2、基于BP、RNN、LSTM、CNN-LSTM算法多特征用电负荷预测
  6.3、基于贝叶斯优化的BP、RNN、LSTM、CNN-LSTM算法电力负荷预测
  6.4、基于粒子群算法优化的BP、RNN、LSTM、CNN-LSTM算法电力负荷预测
  6.5、基于蚁群算法优化的BP、RNN、LSTM、CNN-LSTM算法电力负荷预测
  6.6、基于遗传算法优化的BP、RNN、LSTM、CNN-LSTM算法电力负荷预测
  6.7、基于狼群算法优化的BP、RNN、LSTM、CNN-LSTM算法电力负荷预测
  6.8、基于狼群算法优化的BP、RNN、LSTM、CNN-LSTM算法电力负荷预测
  6.9、基于注意力机制的BP、RNN、LSTM、CNN-LSTM算法电力负荷预测
  6.10、基于transformer算法电力负荷预测