-
二叉搜索树的实现
1.二叉搜索树的概念
概念:二叉搜索树又称二叉排序树,它是一颗空树或者是一颗具有以下特征的二叉树:
- 若它的左子树不为空,则它的左子树上所有的结点值都小于根节点的值。
- 若它的右子树不为空,则它的柚子树上所有的结点值都大于根节点的值。
- 它的左右子树也为二叉搜索树。

如图所示,左子树的结点数值总小于根节点,有子树的结点数值总大于根节点数值。二叉搜索树的三个基本操作
- 插入操作。
- 查找操作。
- 删除操作。
实现操作前需要的相应准备
//实现一个树所需要的节点 static class TreeNode{ public int val; public TreeNode left; public TreeNode right; public TreeNode(int val){ this.val = val; } } //实现树的头结点。 public TreeNode root = null;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
2.查找操作
实现思路
这里的实现思路很简单,只要明确,在二叉搜索树中,左子树的值小于根节点的值小于右子数的值,就很容易实现。
//实现查找方法 public TreeNode search(int val){ //在二叉搜索树中,根左边的元素总是比根右边的元素大 TreeNode cur = root; while(cur != null){ //出现当要查找的值小于当前节点的情况 if(cur.val < val){ cur = cur.right; //出现当前要查找的值大于当前节点的情况 }else if(cur.val > val){ cur = cur.left; }else{ return cur; } } //当全部搜索完后没找到相应的值 return null; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
3.插入操作
操作如图

实现思路首先这里需要定义一个 cur 参数来通过比较来找到适合插入的位置 , 但是 , 由上图所示不难发现 cur 参数随着查找的进行 , 最终会到达被插入的位置 , 导致无法找到其根节点进行插入操作 .
因此 , 我们需要一个 parent 参数来实现对根节点的记录 , 便于后序的插入.
代码实现
//定义cur用来查找位置,定义parent用来定位插入前的位置 TreeNode cur = root; TreeNode parent = null; while(cur != null){ if(cur.val < key){ parent = cur; cur = cur.right; }else if(cur.val > key){ parent = cur; cur = cur.left; }else{ //在找到相同元素的情况下 return false; } } //到达此处表明要将元素插入合适位置 //将元素放到一个结点中 TreeNode node = new TreeNode(key); //判断插入到该节点的右边还是左边 if(key < parent.val){ parent.left = node; }else{ parent.right = node; } return true; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
测试
这里我们以数组元素[5,3,4,1,7,8,2,6,0,9]为例 , 对于二叉搜索树 , 如果进行中序遍历的操作 , 就会出现从小到大依次排列的情况.public static void main(String[] args) { BinarySearchTree binarySearchTree = new BinarySearchTree(); int[] array = {5,3,4,1,7,8,2,6,0,9}; for (int i = 0; i < array.length; i++) { binarySearchTree.insert(array[i]); } binarySearchTree.inOrder(binarySearchTree.root); } public void inOrder(TreeNode root){ if(root == null){ return; } inOrder(root.left); System.out.print(root.val+ " "); inOrder(root.right); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
如图:

4.删除操作
**注:**删除操作相对情况较多 , 实现相对复杂 , 有以下三种大类情况.
设待删除结点为 cur, 待删除结点的双亲结点为 parent
-
cur.left == null
1.cur 是 root,则 root = cur.right
2.cur 不是 root,cur 是 parent.left,则 parent.left = cur.right
3 cur 不是 root,cur 是 parent.right,则 parent.right = cur.right -
cur.right == null
1.cur 是 root,则 root = cur.left
2.cur 不是 root,cur 是 parent.left,则 parent.left = cur.left
3.cur 不是 root,cur 是 parent.right,则 parent.right = cur.left -
cur.left != null && cur.right != null
需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题
图示分析
情况1.
cur 不是 root,cur 是 parent.left

cur 不是 root,cur 是 parent.right

情况2cur 不是 root,cur 是 parent.left
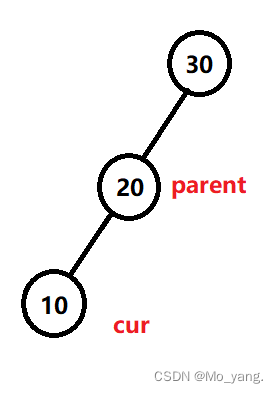
cur 不是 root,cur 是 parent.right

情况3替换法: 如图
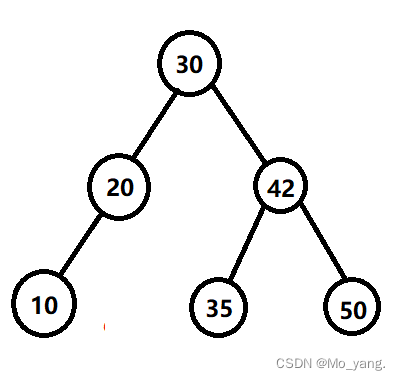
假设这里要删除的元素是 42 .我们已知二叉搜索树有一个规律 , 即 ,左子树小于根节点小于右子树 . 因此 , 通过观察图我们不难发现 , 将右子树 以 42 为根节点以下看做为一颗二叉树 , 想要删除 42 只要将 元素 35 与 42 进行交换即可 , 不难发现 , 这样的替换方法并没有影响到二叉搜索树的规律性.
代码实现
//实现删除方法 public void remove(int key){ TreeNode cur = root; TreeNode parent = null; while(cur != null){ //当找到要删除的元素 if(key == cur.val){ removeNode(parent,cur); return; }else if(key < cur.val){ parent = cur; cur = cur.left; }else{ parent = cur; cur = cur.right; } //当没有找到时返回即可 return; } } private void removeNode(TreeNode parent,TreeNode cur) { //这里删除有三种大情况 //情况1 if (cur.left == null) { //标记结点左节点为NULL的情况时 if (cur == root) { root = cur.right; } else if (cur == parent.left) { parent.left = cur.right; } else { parent.right = cur.right; } //情况2 } else if (cur.right == null) { //标记结点的右节点为NULL时 if (cur == root) { root = cur.left; } else if (cur == parent.left) { parent.left = cur.left; } else { parent.right = cur.left; } } else { //情况3 //左右都不为Null时 TreeNode target = cur.right; TreeNode targetParent = cur; while (target.left != null) { targetParent = target; //一直向左树深入,找到最左端对应的最小的值,替换之后也会满足搜索树的性质 target = target.left; } //进行值得交换 cur.val = target.val; //实现对最后一个元素的跨越 if (target == targetParent.left) { targetParent.left = target.right; } else { targetParent.right = target.right; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
-
相关阅读:
一文带你搞定抖音最近最火的情侣微信早报信息推送
LeetCode解法汇总2698. 求一个整数的惩罚数
神器 SpringDoc 横空出世!最适合 SpringBoot 的API文档工具来了
聚观早报 | vivo Y100官宣;极氪001 FR将上市
嵌入式基础知识-IP地址与子网划分
uniapp开发微信小程序:为什么用户授权信息弹窗没有了?
Stable DIffusion系统教程 | 局部重绘,增删修改的魔法棒
计算机思维基础
web自动化测试(一)之web控件定位
C++ Reference: Standard C++ Library reference: C Library: cmath: erf
- 原文地址:https://blog.csdn.net/qq_62905847/article/details/127741960
