【数据结构与算法】之递归算法

前言

本文为 【数据结构与算法】 递归算法 相关知识，下边将对斐波那契数列、抢5游戏，上台阶问题，汉诺塔问题，树和图的遍历等递归问题进行介绍，帮助大家理解递归算法~

📌博主主页：小新要变强的主页
👉Java全栈学习路线可参考：【Java全栈学习路线】最全的Java学习路线及知识清单，Java自学方向指引，内含最全Java全栈学习技术清单~
👉算法刷题路线可参考：算法刷题路线总结与相关资料分享，内含最详尽的算法刷题路线指南及相关资料分享~
👉Java微服务开源项目可参考：企业级Java微服务开源项目（开源框架，用于学习、毕设、公司项目、私活等，减少开发工作，让您只关注业务！）

---

目录

学习递归之前，我们可以首先思考一下“递推”这个概念？

因为，人的思想是更适合 【递推】 而不是 【递归】。

一、斐波那契数列

1️⃣递推

我们举一个小例子，给出下列的一组数据，那么第10个数字是多少？

1，1，2，3，5，8....
1

正常人的思维肯定是，从前边的数据总结规律，然后从前向后，也就是“自低向上”寻求解决问题的思路，这个过程就是 【递推】 的过程，代码如下：

// 我们传入的n是从1开始计算的，第五个
private static int fibonacci1(int n) {
    // 创建一个数组，用来存放结果
    int[] result = new int[n];
    result[0] = result[1] = 1;
    // 从第三项开始递推，知道第n-1
    for(int i = 2 ; i <= n-1 ; i++){
        result[i] = result[i-1] + result[i-2];
    }
    return result[n-1];
}
1
2
3
4
5
6
7
8
9
10
11

时间复杂度： O(n)。

空间复杂度： O(n)。

2️⃣递归

递归的思路恰恰是相反的，递归的思路是要明确，我们要计算第九个，只要知道第7个和第8个就可以了，以此类推，想要知道第7个就只需要知道第6个和第5个就可以了，一直进行推算直到需要知道第一个和第二个为止。

其实我们可以给这个递推过程推导出一个方程如下，我们可以把他解释为”状态转移方程“：
f ( n ) = { 1 , n = 1 , 2   f ( n − 1 ) + f ( n − 2 ) , n > 2 f(n)=

f(n)={1,n=1,2 f(n−1)+f(n−2),n>2​ 我们甚至可以画出如下的图形：

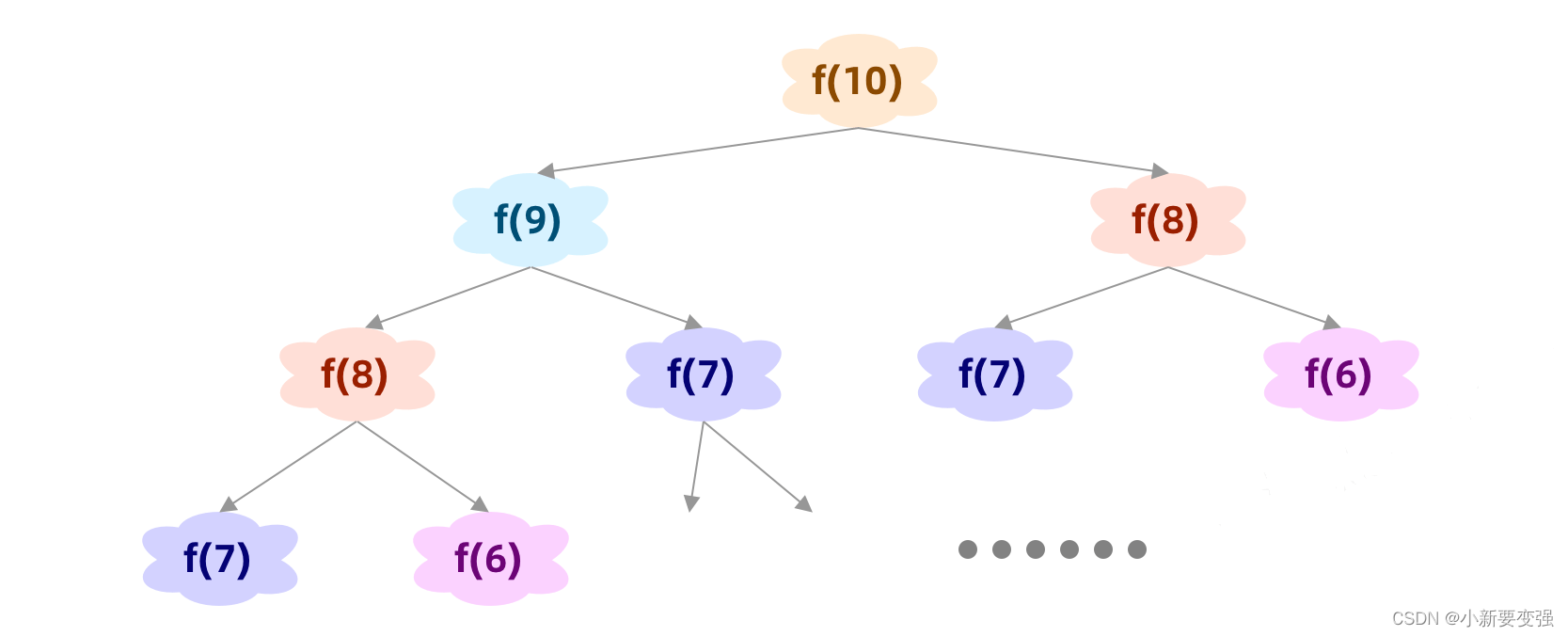
我们可以专门定义一个函数fibonacci2(int n)，这个函数就是用来求第n个斐波那契数列的值的函数，代码如下：

private static int fibonacci2(int n) {
    if (n == 1 || n == 2)
        return 1;
    return fibonacci1(n - 1) + fibonacci1(n - 2);
}
1
2
3
4
5

f(n) = f(n-1) + f(n-2) = f(n-2) + f(n-3) + f(n-3) + f(n-4)，每一项都裂变出两项，最终得出结论：O(2^n)
1

3️⃣重复子问题

我们再一次看看上边的图，会发现一个问题，很多的计算都是重复的，不多说，仅仅是上图中的内容，f(7)出现了3次，f(8)出现了两次，大量的计算是很消耗资源的，那有没有什么办法防止这些重复的计算呢？

我们可以使用一个备忘录，进行存储，每次计算完成之后将结果保存在一个数组（集合）中，代码如下：

// 使用一个数组memo进行保存，memo的下标代表第几个，值就是结果
private static int fibonacci2(int[] memo,int n) {
    // 如果存在就直接返回
    if (memo[n] > 0){
        return memo[n];
    }
    if (n == 0 || n == 1){
        memo[n] = 1;
    } else {
        memo[n] = fibonacci2(memo,n-1) + fibonacci2(memo,n-2);
    }
    return memo[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13

时间复杂度为 O(n)，每一次计算的结果都进行保存，相当于计算n个结果。

4️⃣性能

我们比较一下三种方法的性能：

public static void main(String[] args) {
    long start = System.currentTimeMillis();
    System.out.println(fibonacci1(40));
    long end = System.currentTimeMillis();
    System.out.println(end - start);

    start = System.currentTimeMillis();
    System.out.println(fibonacci2(new int[40],40));
    end = System.currentTimeMillis();
    System.out.println(end - start);

    start = System.currentTimeMillis();
    System.out.println(fibonacci3(40));
    end = System.currentTimeMillis();
    System.out.println(end - start);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

我们会发现，当有了【备忘录】之后，性能得到了大幅度的提升，这就是所谓的【空间换时间】。

二、抢5游戏

两个人先从【数字1或2】中选择一个，然后，另一个人在这个基础上选择加1或者加2，正好加到5为止，如果是你怎么能保证这个游戏必赢呢？

这个问题很简单，我们把各种情况列出来，总能找到答案，因为一共就只有五个数字。

那换一个数字呢，比如20，你会发现，从递推的角度去思考很难得出答案，我先说2 然后…后面有非常多中情况 ，规则虽然很简单，但是这个思路确实不太行得通。此时递归的思路就来了，递归的思路是这个样子的：

-（1）我要是最后必须喊20，就必须让对手喊19或18。
-（2）我只要喊17，就可以让对手喊19或18，至于要倒数第二次喊17就行。
-（3）一次类推，只要我想喊17，上一次就必须是14，在上一次我就是11，以此类推 8 ，5，2
-（4）最后的结论就是只要我先喊2，然后依次5，8，11，14，17，20，我就必胜。

而这个思想就是一个递归的思想，递归的思想有两个明显的妙用：

-（1）只要解决了上一步的问题就能解决下一步的问题，一依次类推就能解决全部的问题。
-（2）推倒的过程是相同的，是可以复制的。

但是，使用递归一定要注意，过程相同，单要有结束条件。

规律： 倒着数，每次减3，最后的结果是2或1时停止：

我们可以下面代码：

public class Game {

    public static void main(String[] args) {
        List<Integer> five = getFive(20, new ArrayList<>());
        System.out.println(five);
    }

    private static List<Integer> getFive(int num,List<Integer> res){
        if (num > 0) {
            res.add(num);
            getFive(num - 3, res);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

结果如下：

三、上台阶问题

一个人上台阶，每次只能上1个或2个台阶，问，有多少种情况可以上到第20个台阶？这个问题其实是斐波那契数列的应用。

前提条件是每次只能上一个或两个台阶，我们要上第20个台阶不外乎就是从第十八个或者第十九个台阶上，也就意味着上第十八个台阶的方式的数量+上第19个台阶的数量之和。

说的简单一点就是，我有x种情况可以上到第18个台阶，我有y种情况可以上到第19个台阶，那么上到第20个台阶的情况就有x+y种。

公式还是：f(n)=f(n-1)+f(n-2)。

四、汉诺塔问题

传说越南河内有一个寺庙，寺庙里有三根柱子，憎侣之间传言如果按照某个规定将64个盘子全部移动另外的柱子上，世界末日也就到了。事实证明，如果僧侣每一秒移动一个，大概需要5800亿年，当然这只是一个传说，这也是汉诺塔（Hanoi就是河内的意思）。

汉诺塔问题的描述：有三个柱子A、B、C，现在有n个盘子，需要从A柱转移到C柱，需要满足一下条件：

• （1）每次只能移动一个盘子
• （2）任何时候小盘子不能放在大盘子下边
• （3）B柱可以用来零时存放盘子，但是依然要满足小盘子不能放在大盘子下边的条件

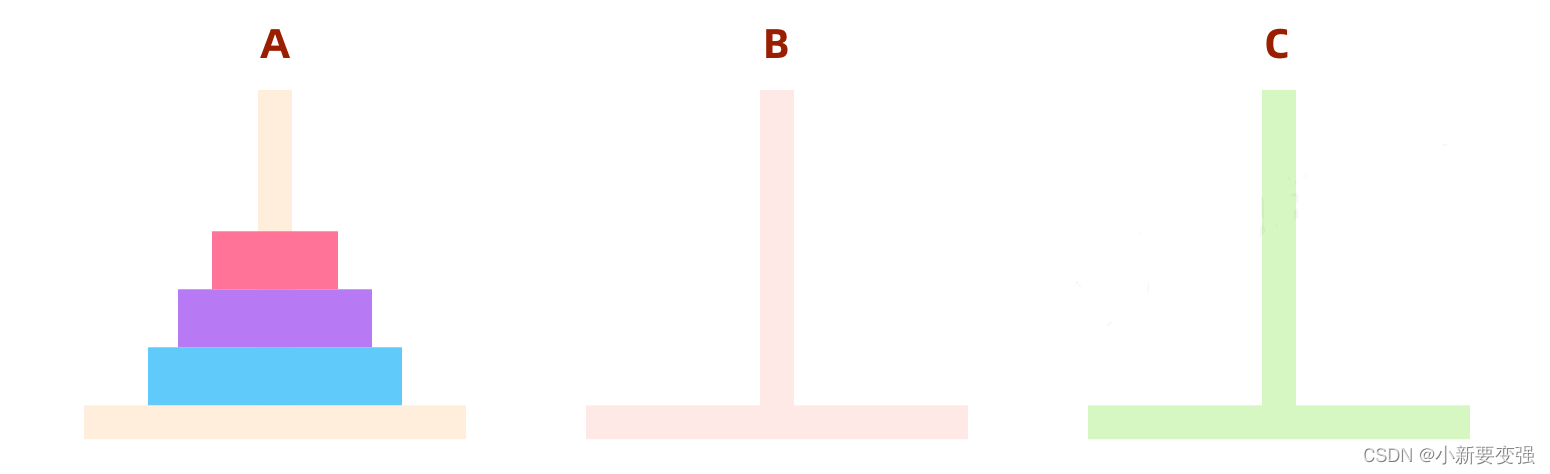
其实，这个游戏我们小时候都玩过，如果只有三个盘子这个游戏是很简单的，但是盘子数量一旦多起来就不是很好处理了：

我们以三个盘子为例，我们不妨简单的玩一下：

• 第一步

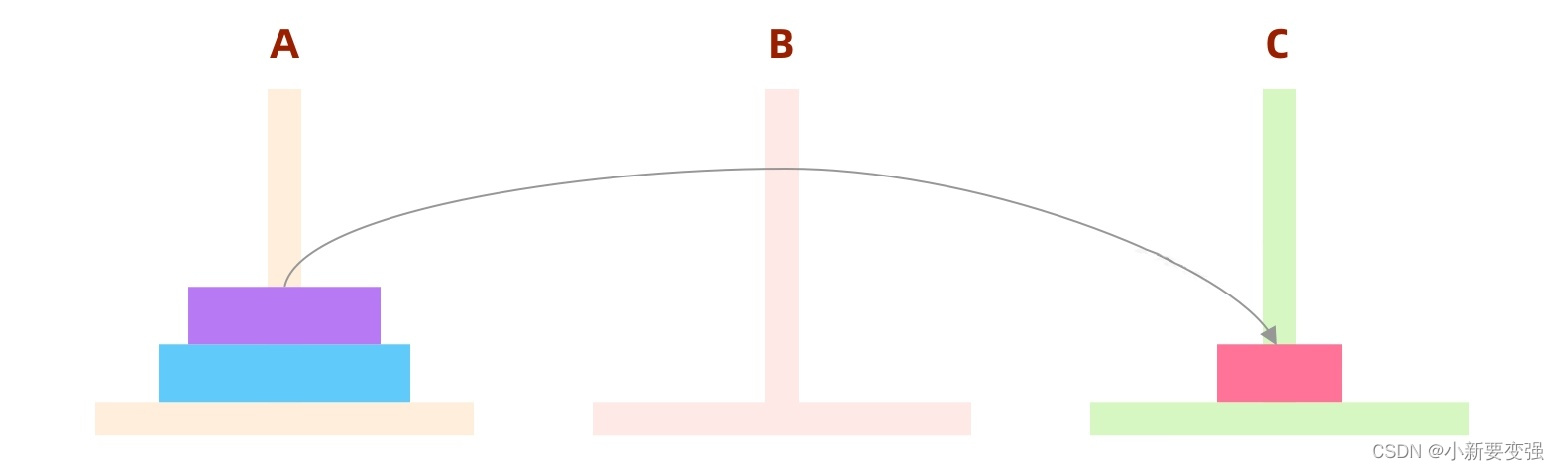
• 第二步

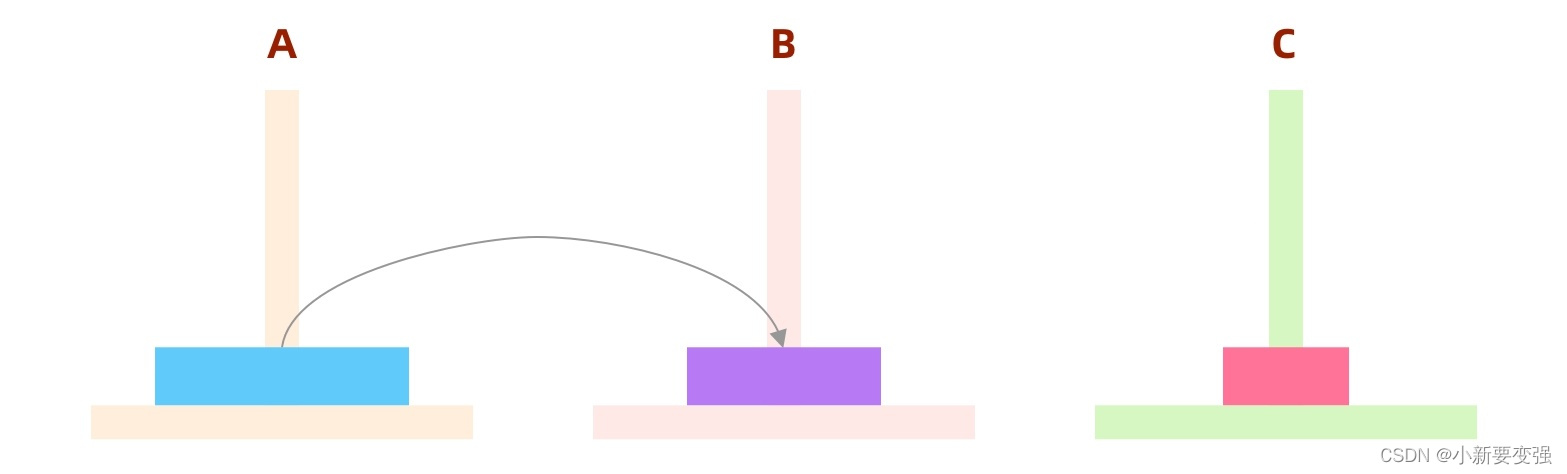
• 第三步

• 第四步

• 第五步

• 第六步

• 第七步

对于三个盘子的汉诺塔来说，还是比较简答的，但是盘子的数量如果增加一杯呢？
如果从递推的角度去思考这个问题，一定要理性的分析一下这个过程中的规律，才能下结论。

但是如果思维反转，用递归来思考呢？

我们要实现64个盘子的汉诺塔，那么要让63个的变成一个什么样子呢？
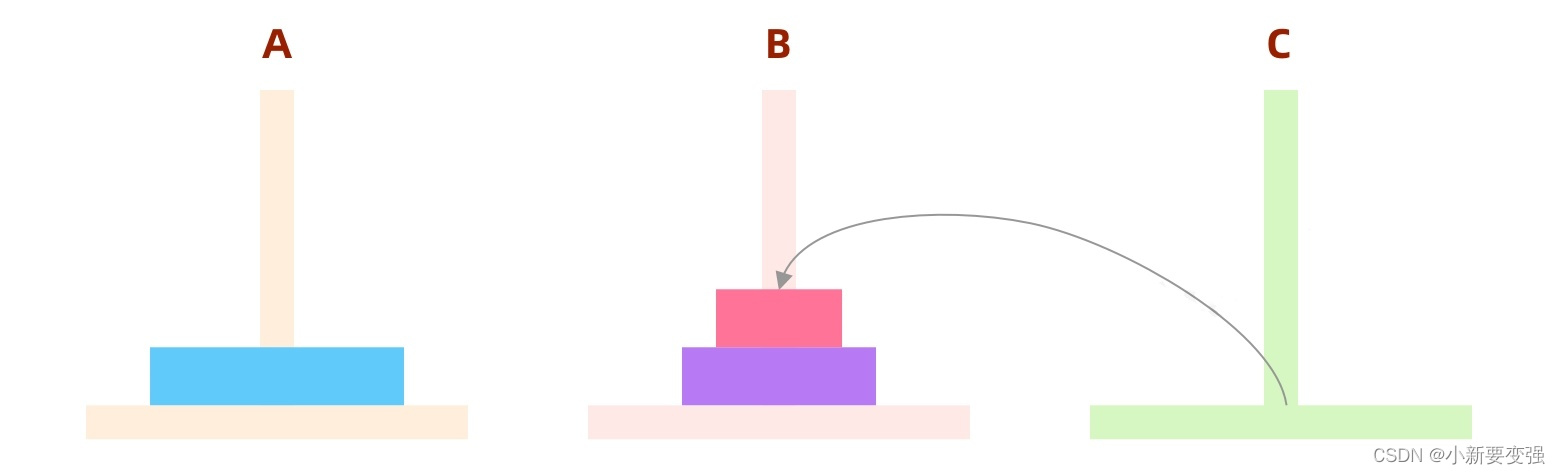
我们要做的就是将前63个移动到B柱，将第64个从A移动到C，此时最大号的盘子就转移成功了：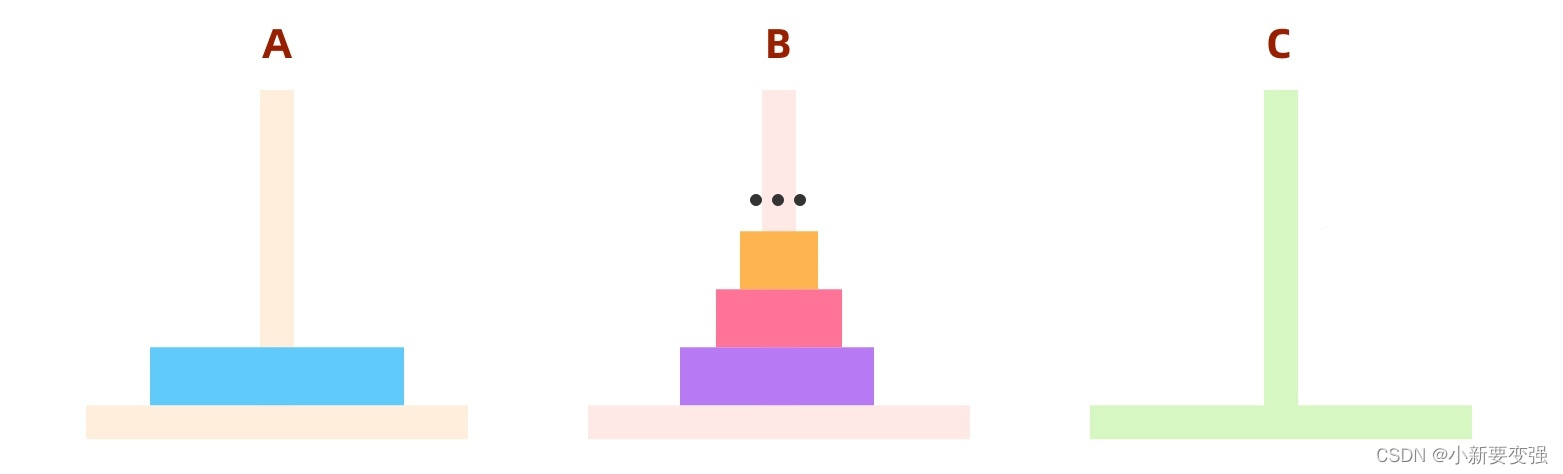

然后我们再将B柱的所有盘子移动到C柱就好了。

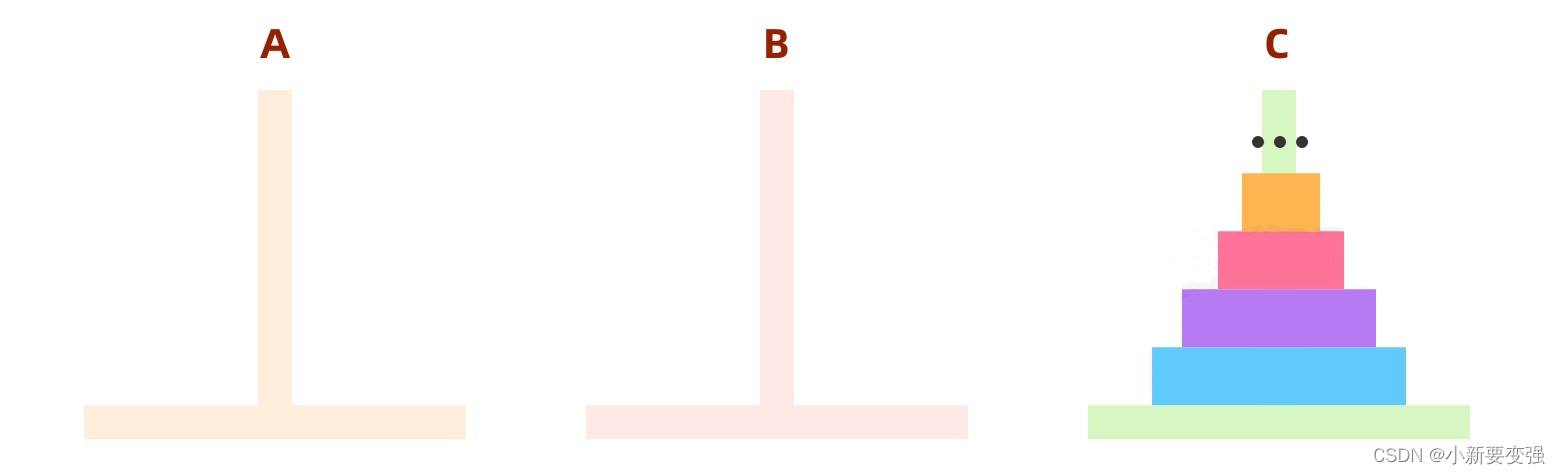
通过这个问题，我们巧妙的将大的问题抽象成一个统一可复制的算法，而计算机最大的优势就在于快速的做出大量的重复性问题。

public class Hanoi {

    public static void main(String[] args) {
        hanoi(3,'A','B','C');
    }

    /**
     * 解决n层汉诺塔问题的方法
     * @param num 盘子的数量
     * @param from 第1根柱子
     * @param temp 第2根柱子
     * @param to 第3根柱子
     */
    public static void hanoi(int num,char from, char temp,char to){
        if(num < 1){
            System.out.println("您输入的数字不合法！");
        }
        if (num == 1){
            System.out.println("将【"+ num +"】个盘子从【"+from+"】转移到【"+to+"】");
        } else {
            //要解决n层汉诺塔的问题，可以将n个盘子分解成（n-1） 1
            // 1、先处理n-1个盘子的汉诺塔问题，从from转移到temp，
            hanoi(num-1,from,to,temp);
            // 2、挪动盘子
            System.out.println("将【"+ num +"】个盘子从【"+from+"】转移到【"+to+"】");
            // 3、再处理一次n-1个盘子的汉诺塔问题，从temp转移到to，
            hanoi(num-1,temp,from,to);
        }

    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

时间复杂度的计算：

用递归来解决汉诺塔问题是非常方便的选择，最后我们来分析一下汉诺塔问题的时间复杂度。 我们很容易得到汉诺塔问题的递推公式，64层汉诺塔，需要将63层的汉诺塔在A和B之间转换两次+最大的盘子移动一次： f ( n ) = { 1 , n = 1   2 f ( n − 1 ) + 1 , n > 1   f(n)=

\ f(n)={1,n=1 2f(n−1)+1,n>1​ 

计算过程：
$$f(n)=2f(n-1)+1=2\ast （2f(n-2)+1）+1=2\ast 2f(n-2)+3=2^{（}n-1）+(1+3+7+...)=2^n-1$$
舍掉常数项，所以汉诺塔问题的时间复杂度为O(2^n)。

五、树和图的遍历

树的遍历，其实本质也是一种递归：

public class RecursiveBinaryTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int v) {
            value = v;
        }
    }


    // 先序打印所有节点
    public static void Preorder(Node root) {
        if (root == null) {
            return;
        }
        System.out.println(root.value);
        Preorder(root.left);
        Preorder(root.right);
    }

    public static void Inorder(Node root) {
        if (root == null) {
            return;
        }
        Inorder(root.left);
        System.out.println(root.value);
        Inorder(root.right);
    }

    public static void Postorder(Node root) {
        if (root == null) {
            return;
        }
        Postorder(root.left);
        Postorder(root.right);
        System.out.println(root.value);
    }

    public static void main(String[] args) {
        Node root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
        root.right.left = new Node(6);
        root.right.right = new Node(7);


        Preorder(root);
        System.out.println("====先序遍历====");
        Inorder(root);
        System.out.println("====中序遍历====");
        Postorder(root);
        System.out.println("====后续遍历====");

    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

使用递归对图进行深度优先遍历，它的结构和之前的栈可能有些不同：

// 使用递归遍历图
public static <T> void recursive(Vertex<T> vertex){
    // 拿到顶点进行遍历操作
    if(!vertex.visited){
        System.out.println(vertex.t);
        vertex.visited = true;
    }
    // 看看当前的顶点时候有邻接节点，如果有执行相同错做
    if(vertex.neighborList != null){
        for (Vertex<T> tVertex : vertex.neighborList) {
            recursive(tVertex);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

---

后记

👉Java全栈学习路线可参考：【Java全栈学习路线】最全的Java学习路线及知识清单，Java自学方向指引，内含最全Java全栈学习技术清单~
👉算法刷题路线可参考：算法刷题路线总结与相关资料分享，内含最详尽的算法刷题路线指南及相关资料分享~
👉Java微服务开源项目可参考：企业级Java微服务开源项目（开源框架，用于学习、毕设、公司项目、私活等，减少开发工作，让您只关注业务！）