【李宏毅机器学习】adversarial attack 对抗攻击

note：

• 对抗训练（adversarial training）通过对抗攻击（adversarial attack）的手段，即生成对抗样本（对部分原样本加入微小的扰动，可能导致误分类），是的NN能适应这种改变，能够有效增强model对对抗样本鲁棒性。而对抗训练的研究一般就是找合适的扰动，如何让模型更具鲁棒性。
• FGSM和FGM区别在于归一化的方法不同，FGSM通过sign函数对梯度采取max归一化，而FGM采用L2归一化。前者max归一化是说如果梯度某个维度上的值为正，则为1，反之为-1；后者L2归一化是说将梯度的每个维度除以梯度的L2范数。
• 根据威胁模型可以将现有的对抗性攻击分为白盒、灰盒和黑盒攻击。这3种模型之间的差异在于攻击者了解的信息。
  • 在白盒攻击的威胁模型中，假定攻击者具有关于其目标模型的完整知识，包括模型体系结构和参数。因此攻击者可以通过任何方式直接在目标模型上制作对抗性样本。
  • 在灰盒威胁模型中，攻击者了解的信息仅限于目标模型的结构和查询访问的权限。
  • 在黑盒威胁模型中，攻击者只能依赖查询访问的返回结果来生成对抗样本。
• 对抗训练借鉴了强化学习的思路，最大化扰动的同时最小化对抗期望风险。对抗训练给NN的随机梯度优化限制了一个李普希茨（Lipschitz）的约束。$$\underset{\theta }{\mathrm{argmin}}{\mathbb{E}}_{(x,y)\sim D}\left[\underset{ϵ\in S}{\max }L(\theta ,x+ϵ,y)\right]$$

零、adversarial attack概念

源自《Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey》section2的adversarial attack概念。

1.1 Adversarial example/image

Adversarial example/image is a modified version of a clean image that is intentionally perturbed (e.g. by adding noise) to confuse/fool a machine learning technique, such as deep neural networks.

对抗样本/图像是干净图像的一个修改版本，它被故意干扰(例如通过添加噪声)来混淆/愚弄机器学习技术，如深层神经网络。

1.2 Adversarial perturbation

Adversarial perturbation is the noise that is added to the clean image to make it an adversarial example.

对抗性扰动是指加到干净的图像中，使其成为一个对抗样本的噪声。

1.3 Adversarial training

Adversarial training uses adversarial images besides the clean images to train machine learning models.

对抗训练是指除了使用干净的图像外，还使用对抗性图像来训练机器学习模型

1.4 Adversary

Adversary more commonly refers to the agent who creates an adversarial example. However, in some cases the example itself is also called adversary.

对抗者更多的是指创造对抗样本的代理人。然而，在某些情况下，这个对抗样本本身也被称为对抗者。

1.5 Black-box attacks & ‘semi-black-box’ attacks

Black-box attacks feed a targeted model with the adversarial examples (during testing) that are generated without the knowledge of that model. In some instances, it is assumed that the adversary has a limited knowledge of the model (e.g. its training procedure and/or its architecture) but definitely does not know about the model parameters. In other instances, using any information about the target model is referred to as ‘semi-black-box’attack. We use the former convention in this article.

黑箱攻击向目标模型提供了不了解该模型而生成的对抗样本(在测试期间)。在某些情况下，假定对抗者对模型的了解有限(例如，训练过程和/或其结构)，但肯定不知道模型参数。在其他情况下，使用任何关于目标模型的信息都被称为“半黑箱”攻击。

1.6 White-box attacks

White-box attacks assume the complete knowledge of the targeted model, including its parameter values, architecture, training method, and in some cases its training data as well.

白箱攻击假定（对抗者）完全了解目标模型，包括其参数值、体系结构、训练方法，在某些情况下还包括其训练数据。

1.7 Detector

Detector is a mechanism to (only) detect if an image is an adversarial example.

检测器是一种用于(仅)检测图像是否是对抗样本的工具。

1.8 Fooling ratio/rate

Fooling ratio/rate indicates the percentage of images on which a trained model changes its prediction label after the images are perturbed.

欺骗率是指一个经过训练的模型在受到干扰后改变其预测标签的图像百分比。

1.9 One-shot/one-step methods & iterative methods

One-shot/one-step methods generate an adversarial perturbation by performing a single step computation, e.g. computing gradient of model loss once. The opposite are iterative methods that perform the same computation multiple times to get a single perturbation. The latter are often computationally expensive.

一次/一步方式通过执行一步计算，例如计算模型损失梯度一次来产生对抗扰动。相反的是迭代方式，它们多次执行相同的计算以获得单个扰动。后者通常在计算上很昂贵。

1.10 Quasi-imperceptible perturbations

Quasi-imperceptible perturbations impair images very slightly for human perception.

准不可察觉的扰动会轻微地损害图像，就人类感知方面而言。

1.11 Rectifier

Rectifier modifies an adversarial example to restore the prediction of the targeted model to its prediction on the clean version of the same example.

整流器（校正器）修改对抗样本，以将目标模型的预测恢复到其对同一示例的干净版本的预测。

1.12 Targeted attacks & non-targeted attacks

Targeted attacks fool a model into falsely predicting a specific label for the adversarial image. They are opposite to the non-targeted attacks in which the predicted label of the adversarial image is irrelevant, as long as it is not the correct label.

目标攻击欺骗了模型，使其错误地预测对抗性图像为特定标签。它们与非目标攻击相反，在非目标攻击中，对抗性图像的预测标记是不相关的，只要它不是正确的标记。

1.13 Threat model

Threat model refers to the types of potential attacks considered by an approach, e.g. black-box attack.

威胁模型是指一种方法所考虑的潜在攻击类型，例如黑匣子攻击。

1.14 Transferability

Transferability refers to the ability of an adversarial example to remain effective even for the models other than the one used to generate it.

可转移性是指对抗性范例即使对生成模型以外的模型也保持有效的能力。

1.15 Universal perturbation & universality

Universal perturbation is able to fool a given model on ‘any’ image with high probability. Note that, universality refers to the property of a perturbation

being ‘image-agnostic’ as opposed to having good transferability.

普遍扰动能够以很高的概率在任意图像上欺骗给定模型。请注意，普遍性是指扰动的性质是“图像不可知论”，而不是具有良好的可转移性。

一、how to attack

如CV中，给原始图像加入微小噪声，想使得训练得到的classifier把猫图识别为[非猫]。如果是non-targeted则是只是输出非猫，如果是targeted类就是classifier输出具体的非猫类别（如小脑虎）。

在威胁模型（白盒、灰盒和黑盒攻击）的框架中，研究者开发了许多用于对抗样本生成的攻击算法，比如基于有限内存的 BFGS（limited-memory Broyden-Fletcher-Goldfarb-Shan-no, L-BFGS）、快速梯度符号法（fast gradient sign method, FGSM）、基本迭代攻击/投影梯度下降（basic iterative attack/projected gradient descent, BIA/PGD）、分布式对抗攻击（distributionally adversarial attack, DAA）、Carlini和Wagner（C&W）攻击、基于雅可比的显著图攻击（Jacobian-based saliency map attack, JSMA）以及DeepFool。尽管这些攻击算法最初是在白盒威胁模型下设计的，但是由对抗样本在模型之间的可传递性可知：它们同样适用于灰盒威胁模型和黑盒威胁模型。

1.1 attack approach

x0为初始图片，x为攻击后（加入人眼无法察觉的噪声）的图片，目标是使得分类器输出的概率分布远离cat的概率分布。其实在NLP中也有使用对抗攻击，如通过对一个句子中的某些词进行同义词替换使得情感分类错误等。

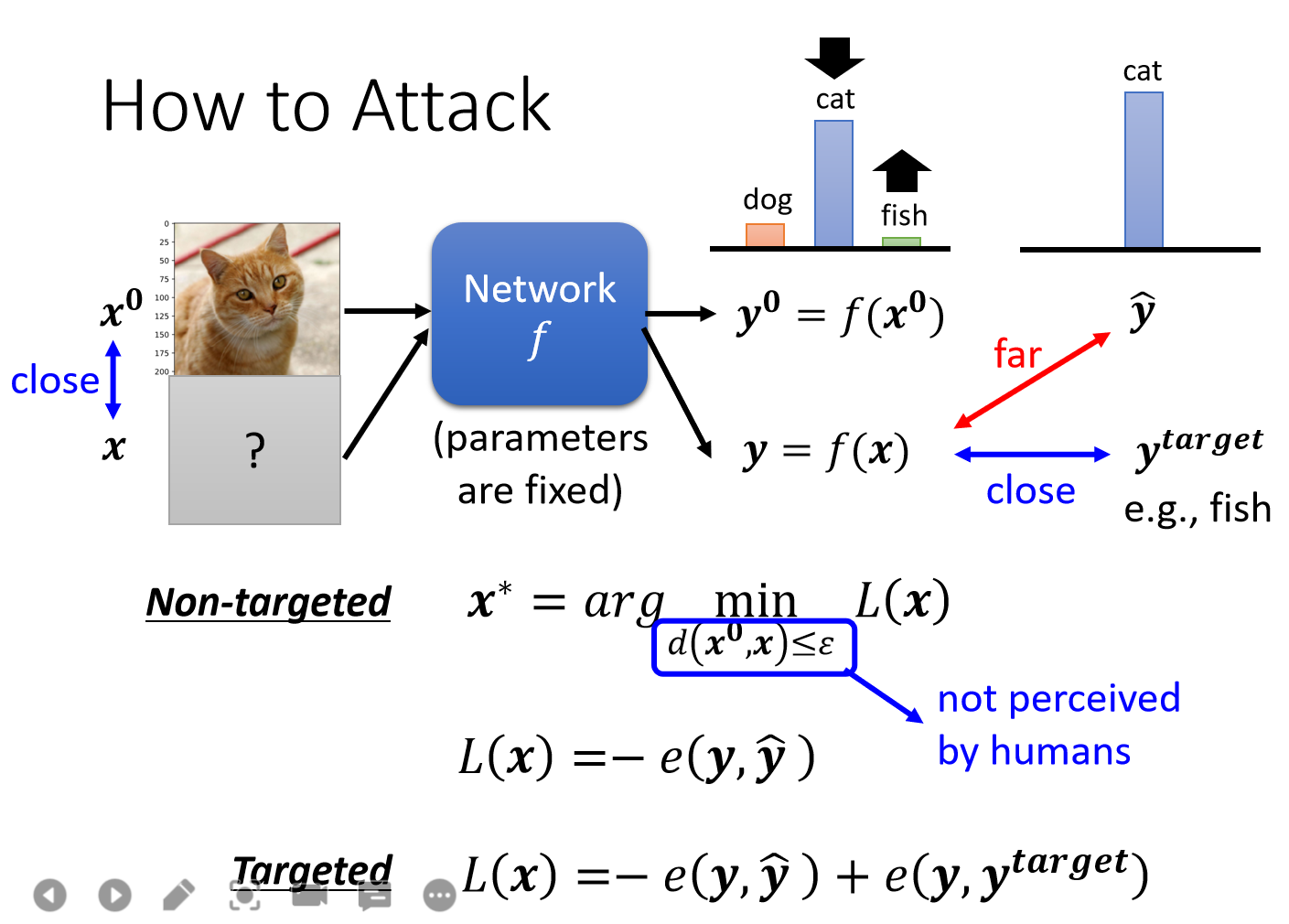
这个问题的loss函数是:Non-targeted: $\mathrm{L}(\mathrm{x})=-\mathrm{e}(\mathrm{y},\hat{\mathrm{y}})$
targeted: 不仅需要 $\mathrm{y}$ 与 $\hat{\mathrm{y}}$ 越远越好, 还要保证 $\mathrm{y}$ 与 ${\mathrm{y}}^{\text{target }}$ 越近越好
$$\mathrm{L}(\mathrm{x})=-\mathrm{e}(\mathrm{y},\hat{\mathrm{y}})+\mathrm{e}\left(\mathrm{y},{\mathrm{y}}^{\text{target }}\right)$$

1.2 Non-perceivable

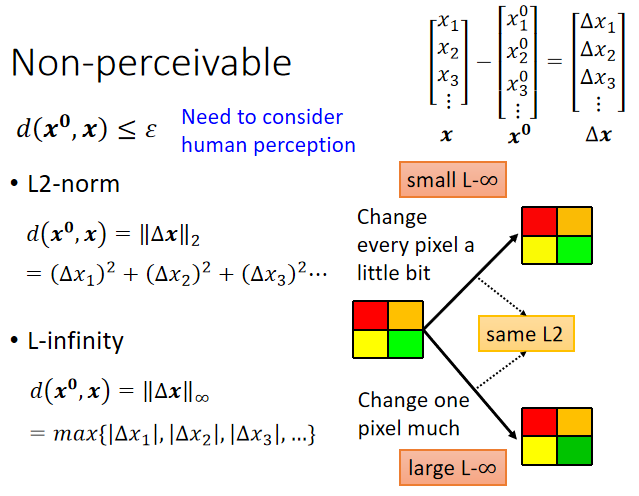
L-infinity norm比L2 norm更能衡量加入噪声后的样本和原始样本之间的距离。

1.3 FGSM和FGM模型

Fast Gradient Sign Method (FGSM) and Fast Gradient Method (FGM)

paper: Explaining and Harnessing Adversarial Examples、Adversarial Training Methods for Semi-Supervised Text Classification

Goodfellow在15年提出的FGSM优化问题如下，主要思想是让扰动的方向沿着梯度提升的方向：
$${\mathrm{x}}^{\ast }=\underset{\mathrm{d}\left({\mathrm{x}}^0,\mathrm{x}\right)\le \epsilon }{\mathrm{argmin}}\mathrm{L}(\mathrm{x})$$
FGSM值更新一次x，并且保证更新后的x满足一定约束。后来17年对FGSM进行修改为FGM（取消符号函数），用F-norm：$${\mathrm{x}}^{\mathrm{t}}\leftarrow {\mathrm{x}}^{\mathrm{t}-1}-\epsilon \frac{\mathrm{g}}{\Vert \mathrm{g}{\Vert }_2}$$

在MIT发的《Towards Deep Learning Models Resistant to Adversarial Attacks》中有下面这幅图，很多生成对抗样本的白盒方法是在原始数据的Lp-norm附近寻找对抗样本，但adversarial training的目标是让原始数据的Lp-norm附近的数据都被分在同一类，因此如果对抗样本处在以原始数据为中心的Lp-norm中，并不会改变分类结果。adversarial training可看做是特殊的正则化regularization（L1、L2正则化限制参数，adversarial training直接“限制”梯度，利用对抗样本进行数据增强）。

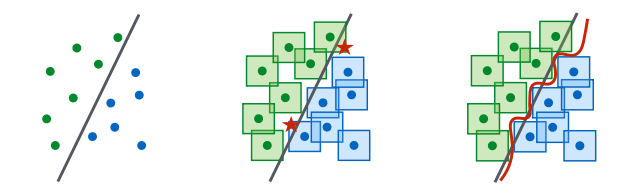
1.4 PGD模型

Projected Gradient Descent (PGD)
paper: Towards Deep Learning Models Resistant to Adversarial Attacks

PGD在生成对抗样本的过程中，使用“小步走，多走几步”的策略，如果走出扰动半径（阈值）的空间，就映射回“球面”，保证扰动不过大。梯度下降求解x时，每次更新x后都检查x是否满足约束，如果不满足约束则进行fix修正。论文中还证明了PGD得到的攻击样本是一阶对抗样本中最强的，但是PGD需要进行T次迭代，即生成一次对抗样本就需要进行T次正向传播和反向传播，所以速度慢。

# 基于pytorch实现的PGD代码实现
class PGD:
    def __init__(self, model, eps=1., alpha=0.3):
        self.model = (
            model.module if hasattr(model, "module") else model
        )
        self.eps = eps
        self.alpha = alpha
        self.emb_backup = {}
        self.grad_backup = {}
 
    def attack(self, emb_name='word_embeddings', is_first_attack=False):
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                if is_first_attack:
                    self.emb_backup[name] = param.data.clone()
                norm = torch.norm(param.grad)
                if norm != 0 and not torch.isnan(norm):
                    r_at = self.alpha * param.grad / norm
                    param.data.add_(r_at)
                    param.data = self.project(name, param.data)
 
    def restore(self, emb_name='word_embeddings'):
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                assert name in self.emb_backup
                param.data = self.emb_backup[name]
        self.emb_backup = {}
 
    def project(self, param_name, param_data):
        r = param_data - self.emb_backup[param_name]
        if torch.norm(r) > self.eps:
            r = self.eps * r / torch.norm(r)
        return self.emb_backup[param_name] + r
 
    def backup_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad and param.grad is not None:
                self.grad_backup[name] = param.grad.clone()
 
    def restore_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad and param.grad is not None:
                param.grad = self.grad_backup[name]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

在更新时, PGM 还会用梯度的 F-norm 作一个 scale, 一次迭代的过程可以写为如下形式：
$$\begin{array}{rl}\mathrm{g}\left({\mathrm{x}}_{\mathrm{t}}\right)& ={\nabla }_{\mathrm{x}}\mathrm{L}\left(\theta ,{\mathrm{x}}_{\mathrm{t}},\mathrm{y}\right)\\ {\mathrm{x}}_{\mathrm{t}+1}& ={\Pi }_{\mathrm{x}+\mathcal{S}}\left({\mathrm{x}}_{\mathrm{t}}+\alpha \mathrm{g}\left({\mathrm{x}}_{\mathrm{t}}\right)/{\Vert \mathrm{g}\left({\mathrm{x}}_{\mathrm{t}}\right)\Vert }_2\right)\end{array}$$
其中, $\mathcal{S}=\left\{\mathrm{r}\mid \mathrm{r}\in {\mathbb{R}}^{\mathrm{d}},\Vert \mathrm{r}{\Vert }_2\le ϵ\right\}$ 为扰动的约束空间, $\mathrm{r}$ 为增加的扰动, $\alpha$ 为步长, ${\Pi }_{\mathrm{x}+\mathcal{S}}$ 用 于将扰动投影到 $ϵ$-ball 上。

1.5 黑盒攻击和白盒攻击

（1）黑盒攻击

黑盒攻击是不知道模型的参数和信息，仅通过model的输入和输出，生成对抗样本，再对网络进行攻击。

黑盒开篇：Practical Black-Box Attacks against Machine Learning

1.单像素攻击

（1）Simple Black-Box Adversarial Attacks on Deep Neural Networks
（2）One Pixel Attack for Fooling Deep Neural Networks

2.基于查询（query-based attack）

基于查询的又可分为基于分数的和基于决策的
socre-based attack
（1）SimBA：Simple Black-box Adversarial Attacks
（2）MetaSimulator：Simulating Unknown Target Models for Query-Efficient Black-box Attacks

decision-based attack
（1）开篇：Decision-Based Adversarial Attacks: Reliable Attacks Against Black-Box Machine learning Models
（2）HSJA：HopSkipJumpAttack: A Query-Efficient Decision-Based Attack
（3）SurFree：SurFree: a fast surrogate-free black-box attack
（4）f-attack：Decision-Based Adversarial Attack With Frequency Mixup

3.基于迁移

（1）开篇：Transferability in Machine Learning: from Phenomena to Black-Box Attacks using Adversarial Samples
（2）Delving into Transferable Adversarial Examples and Black-box Attacks
（3）Enhancing the Transferability of Adversarial Attacks through Variance Tuning
（3）元学习：Meta Gradient Adversarial Attack

4.基于替代

（1）DaST:Data-free Substitute Training for Adversarial Attacks
（2）Delving into Data: Effectively Substitute Training for Black-box Attack
（3）Learning Transferable Adversarial Examples via Ghost Networks

5.其他

（1）通用黑盒攻击UAP：Universal adversarial perturbations
（2）AdvDrop: Adversarial Attack to DNNs by Dropping Information
（3）Practical No-box Adversarial Attacks against DNNs
（4）ZOO: Zeroth Order Optimization Based Black-box Attacks to Deep Neural Networks without Training Substitute Models

（2）白盒攻击

攻击者已知模型的参数等信息，基于给定模型的梯度生成对抗样本，对网络进行攻击。

二、对抗防御

2.1 主动防御 proactive defense

对抗训练

2.2 被动防御 passive defense

在模型前加一个filter（滤波器）

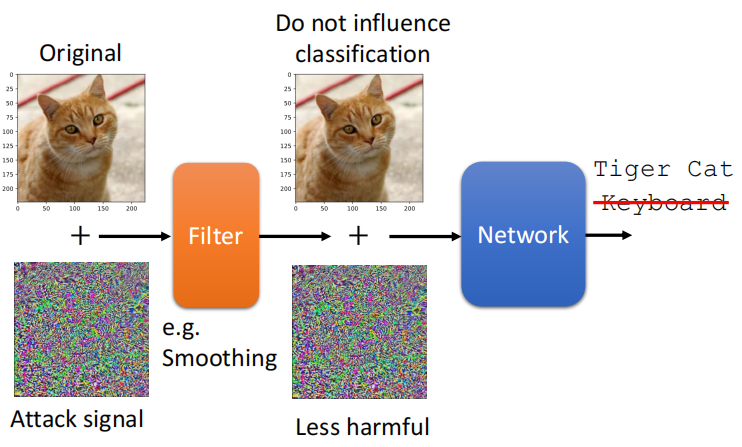
• 图像压缩（先压缩再解压避开攻击）
• Generator（按照对抗样本根据generator生成一张图片）
• Randomization（随机的防御）

四、Adversarial Training in NLP

在NLP中的对抗训练，一般生成对抗样本的做法是把句子中一些词替换成其近义词。可以参考：

[1]马里兰大学在读博士生朱晨: FreeLB—适用于自然语言理解的对抗学习
[2] 某乎：一文搞懂NLP中的对抗训练FGSM/FGM/PGD/FreeAT/YOPO/FreeLB/SMART

五、models list

• FGSM (https://arxiv.org/abs/1412.6572)
• Basic iterative method (https://arxiv.org/abs/1607.02533)
• L-BFGS (https://arxiv.org/abs/1312.6199)
• Deepfool (https://arxiv.org/abs/1511.04599)
• JSMA (https://arxiv.org/abs/1511.07528)
• C&W (https://arxiv.org/abs/1608.04644)
• Elastic net attack (https://arxiv.org/abs/1709.04114)
• Spatially Transformed (https://arxiv.org/abs/1801.02612)
• One Pixel Attack (https://arxiv.org/abs/1710.08864)

Reference

[1] 李宏毅21版视频地址：https://www.bilibili.com/video/BV1JA411c7VT
[2] 李宏毅ML官方地址：http://speech.ee.ntu.edu.tw/~tlkagk/courses.html
[3] https://github.com/unclestrong/DeepLearning_LHY21_Notes
[4]《Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey》section2
[5] 功守道：NLP中的对抗训练 + PyTorch实现
[6] https://blog.csdn.net/weixin_42437114/article/details/120306567
[7] 深度学习中的对抗性攻击都有哪些？怎么防御？
[8] 某乎：一文搞懂NLP中的对抗训练FGSM/FGM/PGD/FreeAT/YOPO/FreeLB/SMART
[9] Towards Deep Learning Models Resistant to Adversarial Attacks. MIT
[10] adversarial training为什么会起作用
[11] Adversarial Attack (对抗攻击)
[12] Towards Understanding and Boosting Adversarial Transferability from a Distribution Perspective. TIP
[13] TIP 2022！阿里提出：从分布视角出发理解和提升对抗样本的迁移性

附：时间安排