算法---分组的最大数量

题目

给你一个正整数数组 grades ，表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组，其中分组间的顺序满足以下全部条件：

第 i 个分组中的学生总成绩 小于 第 (i + 1) 个分组中的学生总成绩，对所有组均成立（除了最后一组）。
第 i 个分组中的学生总数 小于 第 (i + 1) 个分组中的学生总数，对所有组均成立（除了最后一组）。
返回可以形成的 最大 组数。

示例 1：

输入：grades = [10,6,12,7,3,5]
输出：3
解释：下面是形成 3 个分组的一种可行方法：

• 第 1 个分组的学生成绩为 grades = [12] ，总成绩：12 ，学生数：1
• 第 2 个分组的学生成绩为 grades = [6,7] ，总成绩：6 + 7 = 13 ，学生数：2
• 第 3 个分组的学生成绩为 grades = [10,3,5] ，总成绩：10 + 3 + 5 = 18 ，学生数：3
  可以证明无法形成超过 3 个分组。
  示例 2：

输入：grades = [8,8]
输出：1
解释：只能形成 1 个分组，因为如果要形成 2 个分组的话，会导致每个分组中的学生数目相等。

提示：

1 <= grades.length <= 105
1 <= grades[i] <= 105

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-number-of-groups-entering-a-competition
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解决方法

假如我们对数组进行排序
这样的话
第一个数肯定小于 第二三个数的和 第二三的数的和肯定小于第四第五第六的和。。。
我们就可以求出来最多可以分几组
其实就相当于
1 + 2 + 3…x = 数组的长度(计作n)
我们求出来x 就知道一共有多少组了
根据高斯数学公式：
1 + 2 + 3…x = x(x+1)/2
则：

x(x+1)/2 = n
x*x + x -2n = 0
1
2

根据一元二次方程公示

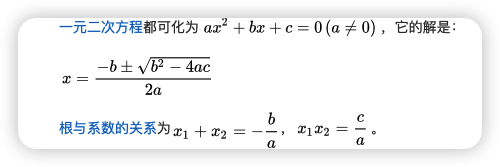
x = ((-1) + Math.sqr(1+8n) )  /  2
1

所以算法为：

    fun maximumGroups(grades: IntArray): Int {
        val size = grades.size
        return ((-1 + Math.sqrt((1 + 8*size).toDouble())) / 2).toInt()
    }
1
2
3
4

总结

1.高中的时候绝对是编程的最好时机 数学确实是很厉害的一门科学
高斯确实牛
2.前一段时间。一直在忙着装H苹果. 算法有点拉下了。 继续努力