-
到底什么是上采样、下采样
上采样
语义分割/实例分割等任务,由于需要提取输入图像的高层语义信息,网络的特征图尺寸一般会先缩小,进行聚合;这类任务一般需要输出于原始图像大小一致的像素级分割结果,因而需要扩张较小的特征图这就用到了上采样
上采样常见方法
常见上采样方法有双线性插值、转置卷积、unpooling
常用的是双线性插值和转置卷积双线性插值
双线性插值:顾名思义就是在两个方向分别进行一次线性插值(要求一个坐标的像素值,先去找他四个周围已知像素的坐标,通过两次单线性插值,得到他的像素值)
单线性插值:
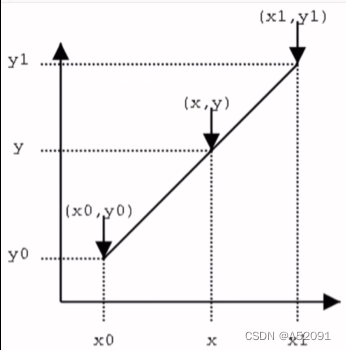
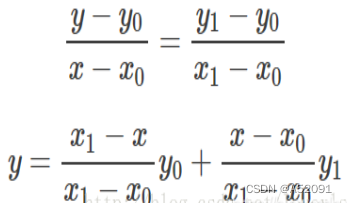
将距离作为权重对y0与y1进行加权双线性插值:
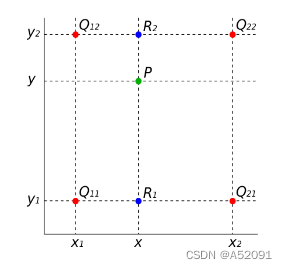
已知的红色数据点与待插值得到的绿色点假如我们想得到未知函数 f 在点P= (x,y) 的值,假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。
首先在x方向进行线性插值,得到R1和R2,然后在y方向进行线性插值,得到P.
这样就得到所要的结果f(x,y).其中红色点Q11,Q12,Q21,Q22为已知的4个像素点.
第一步:X方向的线性插值,在Q12,Q22中插入蓝色点R2, Q11,Q21中插入蓝色点R1;
第二步 :Y方向的线性插值 ,通过第一步计算出的R1与R2在y方向上插值计算出P点。线性插值的结果与插值的顺序无关。首先进行y方向的插值,然后进行x方向的插值,所得到的结果是一样的。双线性插值的结果与先进行哪个方向的插值无关
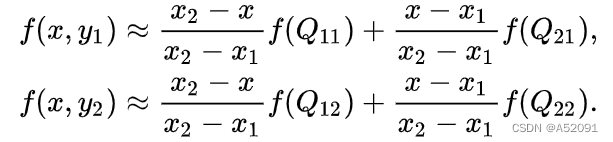
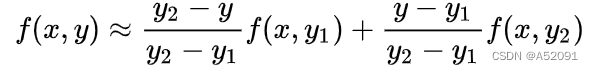
转置卷积
转置卷积(Transposed Convolution) 在语义分割或者对抗神经网络(GAN)中比较常见,其主要作用就是做上采样(UpSampling

对于普通的卷积操作可以形式化为一个矩阵乘法运算
其中卷积核可以通过一个稀疏矩阵表示,其是由卷积核,滑动步长决定的常对角矩阵,维度为d1*d2 (d1为输出的维度(展平为一维向量的形式);d2为输入的维度(展平为一维向量的形式))
每一行向量表示在一个位置的卷积操作,0填充表示卷积核未覆盖到的区域。
将输入X展平为向量则:


同时根据矩阵运算的求导知识可以知道
转置卷积的信息正向传播与普通卷积的误差反向传播所用的矩阵相同
普通卷积的信息正向传播与转置卷积的误差反向传播所用矩阵相同由上可知转置卷积就是一个对输入数据进行适当变换(上采样/补零)的普通卷积操作
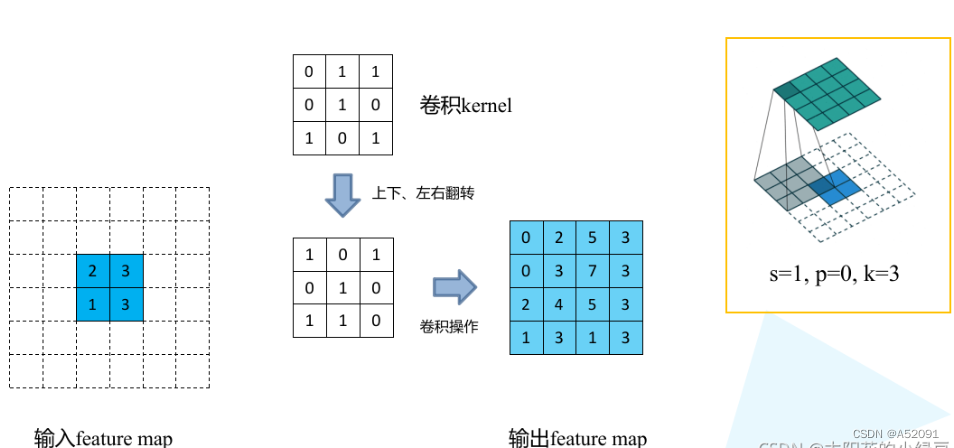
在具体实现是对应的卷积操作如下:
(S表示滑动步长(Sw,Sh),K表示转置卷积核大小,P表示转置卷积的padding)- 对输入的特征图进行扩张(上采样):相邻的数据点之间,在水平方向填充Sw-1个零,在垂直方向填充Sh-1个零
- 对输入特征图进行边界填充:四周分别填充K-P-1零行
- 将卷积核参数上下、左右翻转
- 做正常卷积运算
unpooling
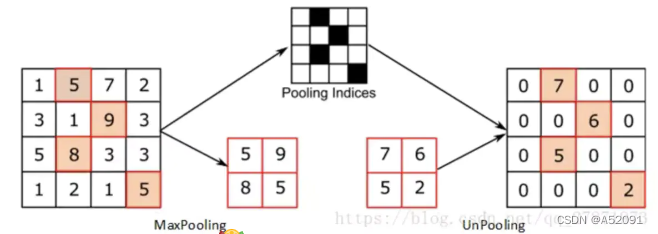 unpooling记录了原来pooling是取样的位置,在unpooling的时候将输入feature map中的值填充到原来记录的位置上,而其他位置则以0来进行填充。
unpooling记录了原来pooling是取样的位置,在unpooling的时候将输入feature map中的值填充到原来记录的位置上,而其他位置则以0来进行填充。下采样
下采样通常来讲也叫做抽取,比如从多数集中抽取少部分
下采样在图像领域实际上就是缩小图像,主要目的是为了使得图像符合显示区域的大小,生成对应图像的缩略图。比如说在CNN中的池化层或卷积层就是下采样。不过卷积过程导致的图像变小是为了提取特征,而池化下采样是为了降低特征的维度。下采样层有两个作用:
一是减少计算量,防止过拟合;
二是增大感受野,使得后面的卷积核能够学到更加全局的信息。下采样常见方法
1 池化:如Max-pooling和Average-pooling,目前通常使用Max-pooling,因为他计算简单而且能够更好的保留纹理特征;
2 卷积 -
相关阅读:
数据结构—归并排序-C语言实现
勒索病毒最新变种.halo勒索病毒来袭,如何恢复受感染的数据?
GUI编程--PyQt5--控件
Apache Doris物化视图使用详解
常用设计模式
一款可自动跳广告的安卓App开源项目
spring中@Component注解有什么功能呢?
JVM概述
【软件与系统安全】栈溢出利用的分析
猿创征文 |《深入浅出Vue.js》打卡Day4
- 原文地址:https://blog.csdn.net/A52091/article/details/127736202