matplotlib如何画球

matplotlib如何画球

数学知识

计算机一般来说不善于处理隐函数，因此需要把隐函数转化一下，一般来说会转化为参数方程，以球体为例，球体的方程就是一个隐函数，但是我们知道球的参数方程，这就很简单了。

球的标准方程：

$x^2+y^2+z^2=10$

球的参数方程：

$x=r\sin \phi \cos \theta$

$y=r\sin \phi \sin \theta$

$z=r\cos \phi$

$(其中0\le \theta \le 2\pi ,0\le \phi \le \pi )$

matplotlib代码

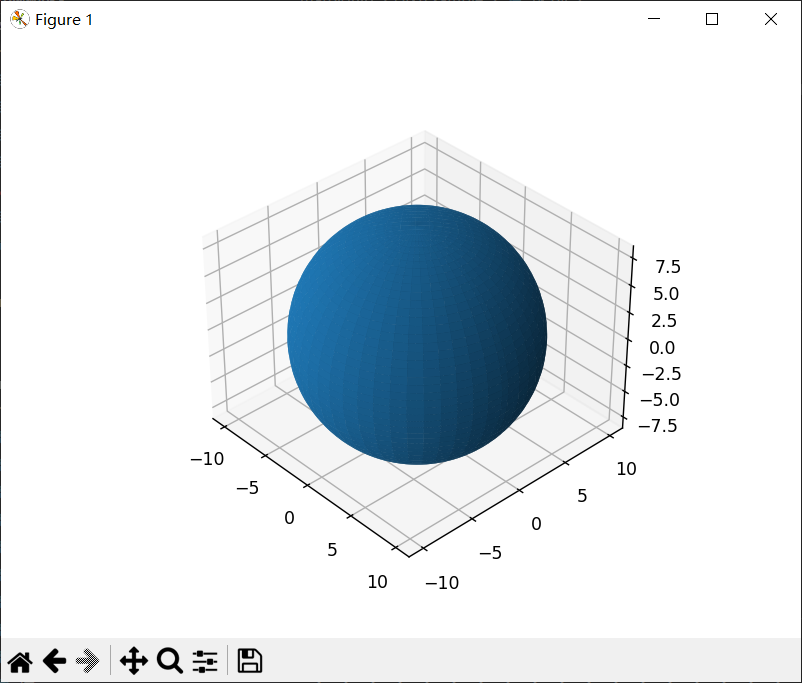
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.animation as animation

fig = plt.figure()
ax = fig.add_subplot(projection='3d')

u = np.linspace(0, 2 * np.pi, 100)# 用参数方程画图
v = np.linspace(0, np.pi, 100)
x = 10 * np.outer(np.cos(u), np.sin(v))# outer()外积函数：返回cosu × sinv
y = 10 * np.outer(np.sin(u), np.sin(v))# 
z = 10 * np.outer(np.ones(np.size(u)), np.cos(v))# ones()：返回一组[1,1,.......]

ax.plot_surface(x, y, z)

ax.set_aspect('equal')
print(np.ones(np.size(u)))
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18