-
【概率论与数理统计】第二章知识点复习与习题
思维导图
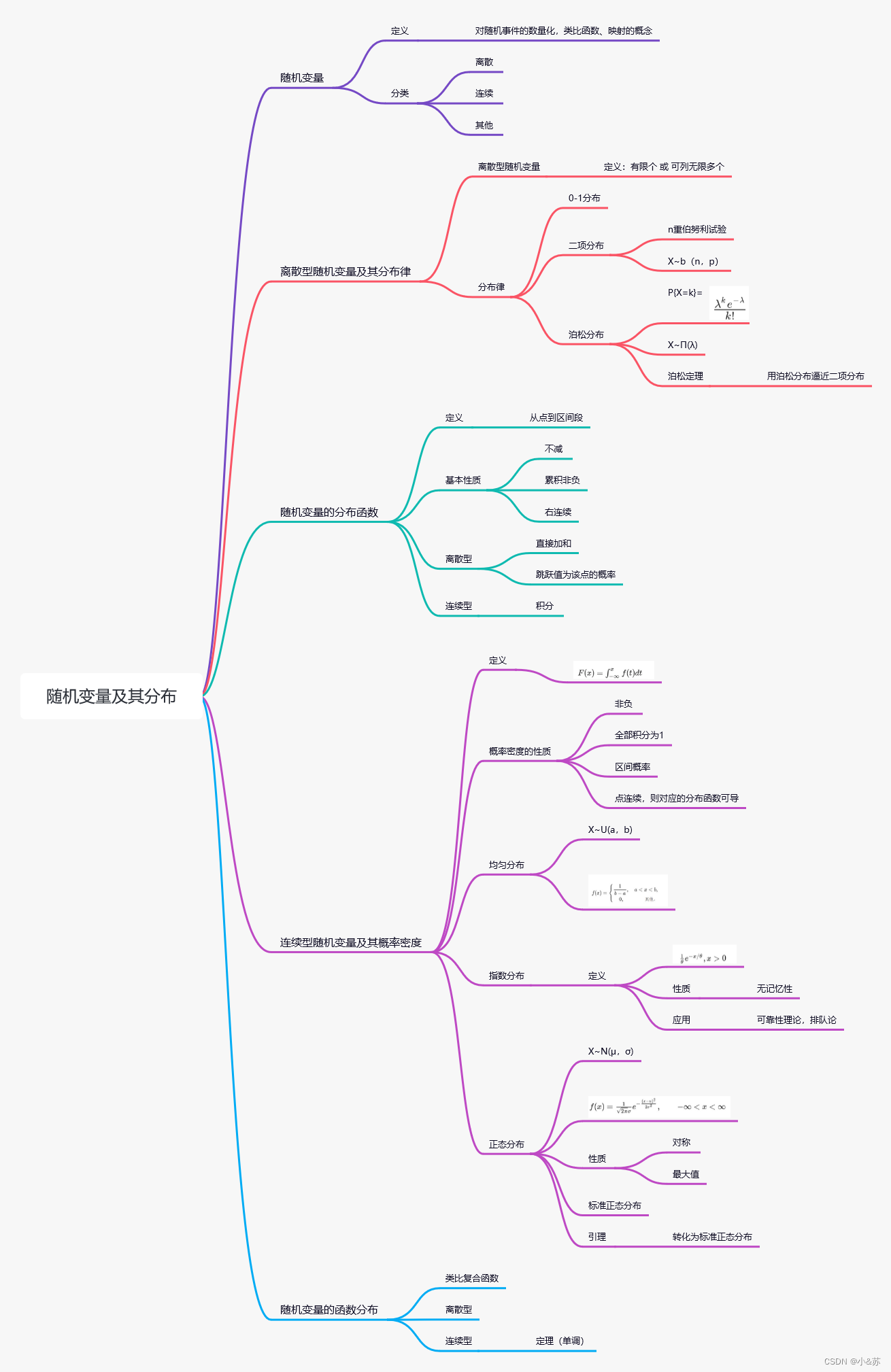
笔记
一、随机变量
定义:设随机试验的样本空间为S={e},X=X(e)是定义在样本空间S上的实值单值函数。称X=X(e)为随机变量。
类似于函数、映射的概念。
既然类似于函数,就有定义域和至于,通过定义知道,定义域为样本空间,值域为实数集。
即对随机事件数量化。二、离散型随机变量及其分布律
1离散型随机变量
定义:全部可能取到的值是有限个或可列无限多个的随机变量。
这里有限一定可列,可列不一定有限。
而分布律的定义则是指:X取各个可能值的概率情况。2分布律
教材中提及的离散型随机变量的分布律有三种,分别为0-1分布,二项分布以及泊松分布
0-1分布
即两点分布,随机变量X只可能取0和1两个值。分布律表达式为
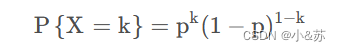 K=0,1
K=0,1
(0伯努利试验、二项分布
和0,1分布类似。
伯努利试验:设实验E只有两个可能结果,A与非A。
设
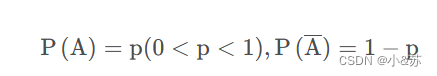
将E独立重复进行n次,即为n重伯努利试验。
这里的独立重复和第一章的一样。二项分布
以X表示n重伯努利试验中事件A发生的次数,X的所有取值为k,根据这个可以得到
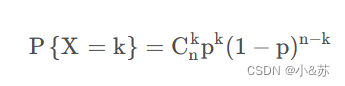
称X服从参数为n,p的二项分布,记为X~b(n,p)
特别地,当n取1时,记为0-1分布。泊松分布
设随机变量X所有可能取值为0,1,2,…,而取各个值的概率
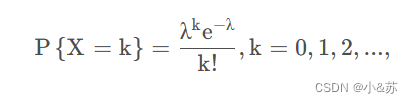 之中λ>0是常数,称X服从参数为λ的泊松分布,记为
之中λ>0是常数,称X服从参数为λ的泊松分布,记为
X~Π(λ)
泊松分布可以用来逼近二项分布,因为二项分布虽然规律性很强,也有比较好的准确性,但是计算的复杂度太高,所以往往会使用泊松分布来逼近。泊松定理:
设λ是一个常数,n是任意正整数,设
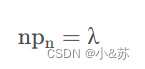 则对于任一固定的非负整数k,有
则对于任一固定的非负整数k,有
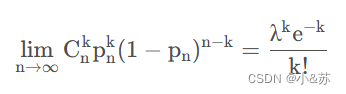
三 、随机变量的分布函数
分布函数的提出是因为在某些情况下,随机变量取实数域上的一点的概率是困难且无意义的,这里点名连续型随机变量,因此改为选取区间的概率。区间一般以左开右闭的形式。
定义
设X是一个随机变量,x是任意实数,函数
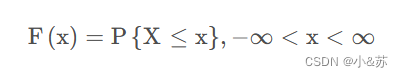 称为X的分布函数
称为X的分布函数
而对于任意实数x1,x2(x1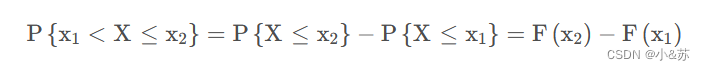
所以,如果已知X的分布函数,就可以知道X落在任意区间上的概率,这种由点到区间的进步,也更加方便我们研究概率,同时也更完整地描述随机变量的统计规律性。
基本性质:
分布函数F(X)具有以下性质
1、他是一个不减函数,即,对于任意实数 x1, x2 (x1 < x2) 有
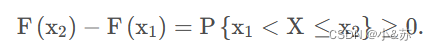
2、
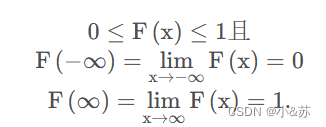
3、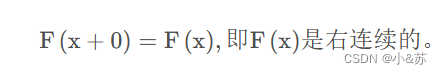
简单概括就是单调不减,累积非负,右连续。
所以结合定义和性质可知:分布函数其实是一种累积概率,有点类似于算法中的前缀和。离散型
一般,设离散型随机变量X的分布律为
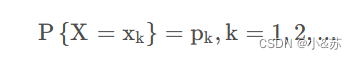
由概率的可列可加性,得
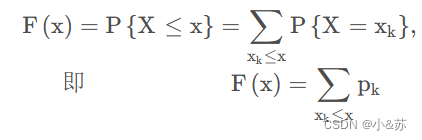
对于离散型,分布函数作为一个累积函数,会存在跳跃,不难发现:跳跃值为该点的概率值连续型
设f(x)为随机变量的概率密度,有

四、连续型随机变量及其概率密度
定义
对于随机变量X的分布函数F(X),存在非负可积函数f(x),使对于任意实数x有
 称X为连续型随机变量,f(x)为X的概率密度函数,简称概率密度。
称X为连续型随机变量,f(x)为X的概率密度函数,简称概率密度。
如果原函数即分布函数连续,则概率密度函数也连续。概率密度的性质
1、非负性
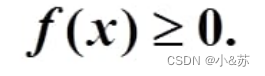 2、
2、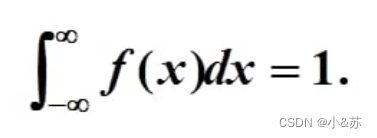
(前两个条件是概率密度的充分必要条件)
3、
三种常见的连续型随机变量
主要用他们的概率密度来描述。
1.均匀分布
定义
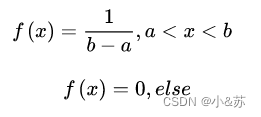 记作X~U(a,b)
记作X~U(a,b)
在a~b的区间上,随机变量落在任一点的概率是等同的,概率只与子区间的长度有关,与子区间的位置无关。分布函数
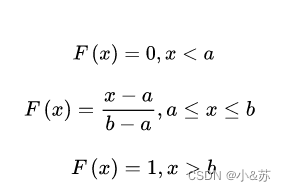
2.指数分布
定义

分布函数
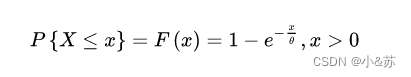
性质
任意s,t>0,有
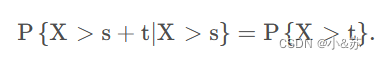
这种性质称为无记忆性。
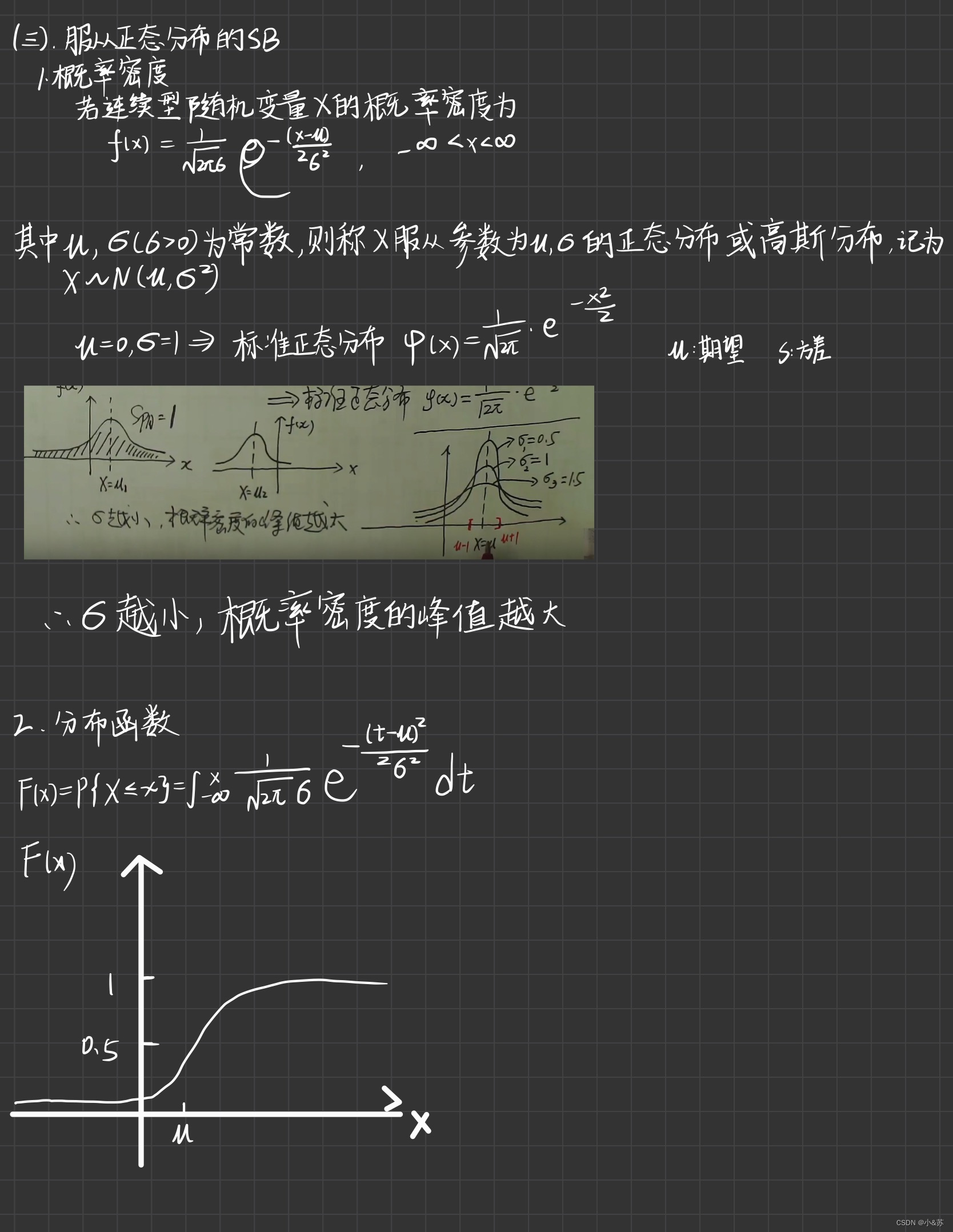
指数分布在可靠性理论与排队理论中有广泛的应用。3.正态分布
 的正态分布或高斯分布,记为
的正态分布或高斯分布,记为
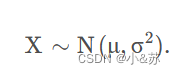
性质
f(x)的曲线具有以下性质:
1.曲线关于μ对称。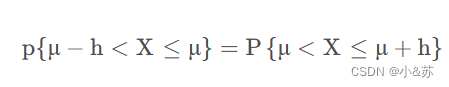
2.当x=μ时取到最大值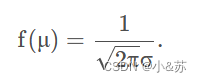
x 离 μ越远,f(x)的值越小。这表明对于同样长度的区间,当区间离μ越远时,X落在这个区间上的概率越小。
特别地,当μ = 0时,σ=1时 称随机变量 X 服从 标准正态分布。其概率函数和概率密度函数分别用 φ(x)和 Φ(x)表示。五、随机变量的函数的分布
关于连续型随机变量的函数有以下定理
设随机变量x具有概率密度
fx(X)
又设函数 g(x) 处处可导且恒有 g’(x) > 0 (或恒有 g’(x) < 0), 则 Y=g(X) 是连续随机变量,概率密度为:
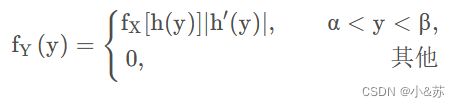
其中 α = min{g(-∞), g(∞)},β = max{g(-∞), g(∞)},h(y) 是 g(x) 的反函数。课后习题

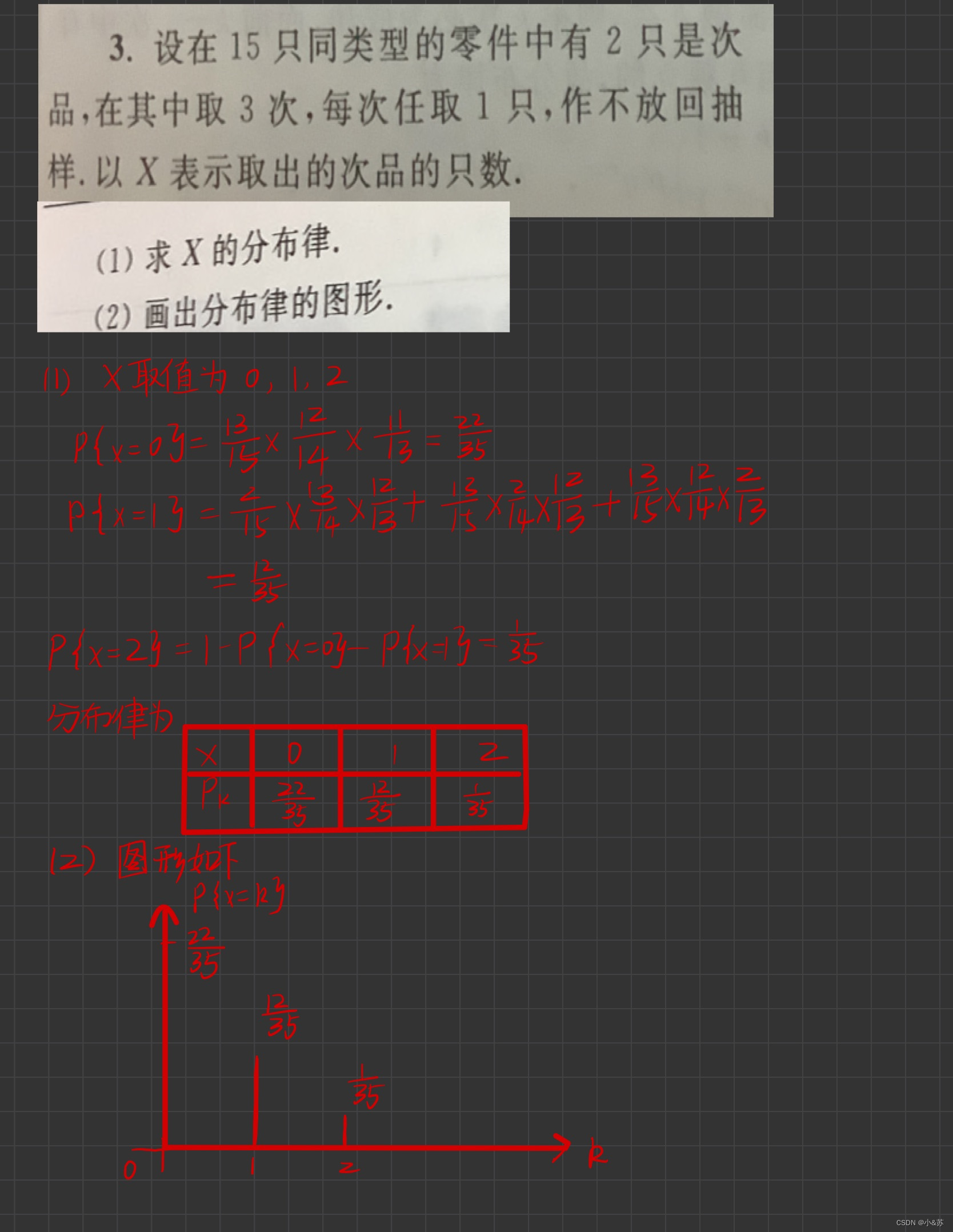



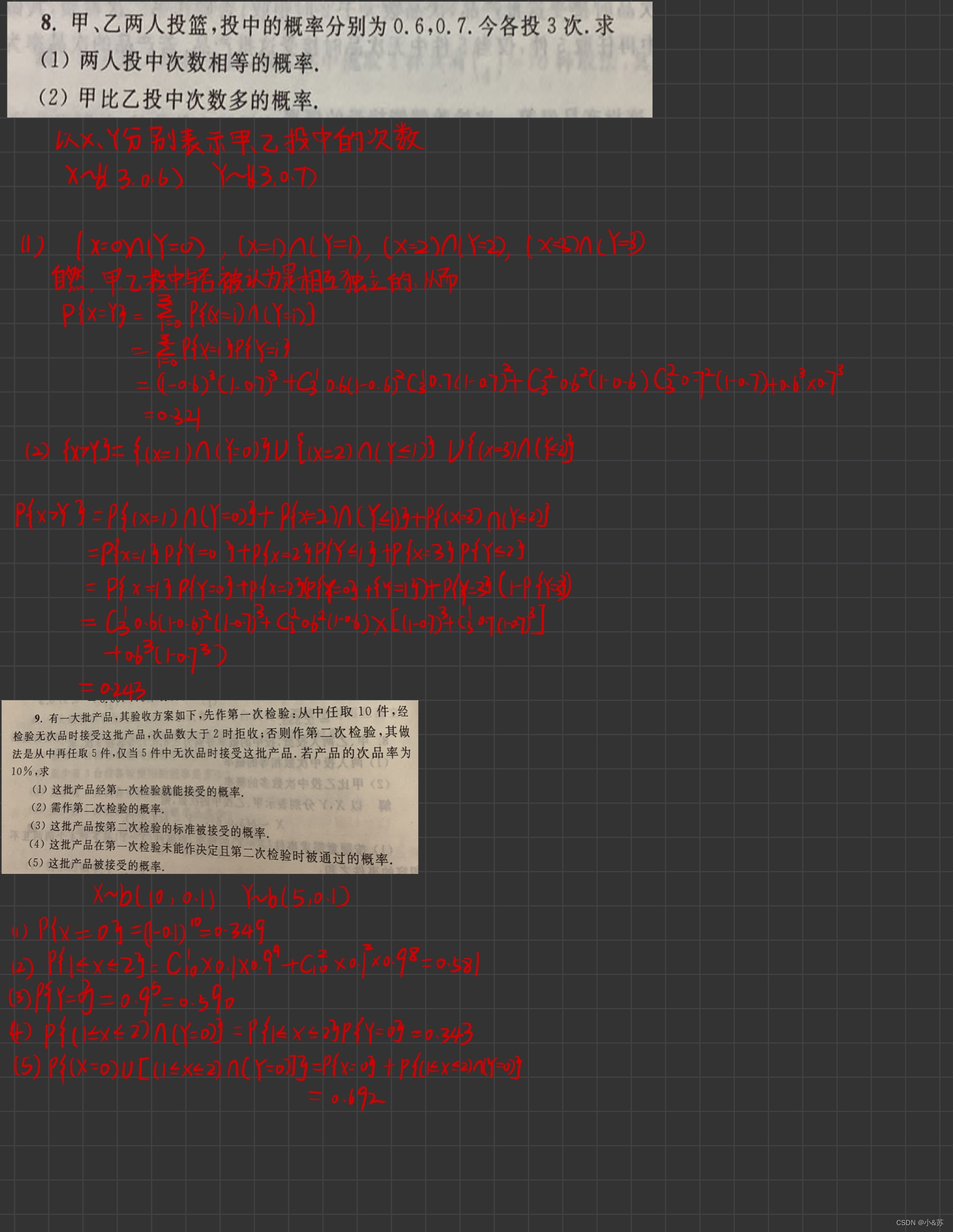














手写笔记
















-
相关阅读:
oracle中使用rownum作为条件的失效问题的原因和解决方法
20个非常有用的单行Python代码片段
二百零六、Flume——Flume1.9.0单机版部署脚本(附截图)
window mysql忘记密码解决方案
信号完整性分析基础知识之有损传输线、上升时间衰减和材料特性(十):有损传输线在时域中的表现
LeetCode-3. 无重复字符的最长子串-Java-medium
直击固定资产管理痛点,让企业轻松管理海量固定资产
threejs(12)-着色器打造烟雾水云效果
新建一个默认的React项目
帐篷出口欧洲需要做哪些检测认证?
- 原文地址:https://blog.csdn.net/manerzi/article/details/127580891