C/C++高精度运算（大整数运算）

前言

高精度的运算在算法题尤为常见，在处理一些大型数据的项目中也需要用到。虽然Boost库中有处理高精度问题的模板，但是标准库中并没有。为了方便学习，本文提供了高精度运算的模板，供大家参考。

---

什么是大整数 

众所周知，最大的整型long long的范围是【-9223372036854775808~9223372036854775807】，即使是无符号位的unsigned long long最大值也只是扩大一倍，那当题目需要用到或需要输出比long long类型的范围还要大的数字时，我们是不是就不能用常规办法去接收这些数字了。这个时候使用大整数就可以解决上述问题——也就是解决接收超出整型范围数字的问题。

大整数的表示

其实大整数的表示方法也不难，我们使用数组就可以了（当然C++的vector容器也是可以的，原理都一样，但为了照顾C语言的小伙伴，本文用数组表示）。

假设现在有一个int类型数组d[1000]，那么我们可以用数组中的每一位元素表示大整数中的每一位数字，比如有整数123456789，那么我们可以用d[0]表示亿位上的【1】，用d[1]表示千万位上的【2】...以此类推，我们就可以用一个长度为9的数组表示这个大整数了。

当然为了契合我们后面四则运算的思维，我们将数组元素的顺序翻转一次，也就是在数组靠前的元素表示低位，而靠后的元素表示高位（原因后面会讲到），也就是如下图所示：

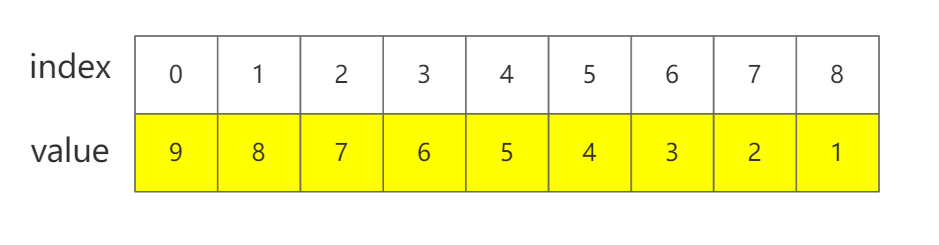
而为了方便我们获取当前大整数的长度，我们可以使用一个结构体（或者一个类，与C语言的结构体不同，在C++中的结构体也可以定义成员函数）来表示。

//struct of bign(big number)
struct bign {
    int d[1000];
    int len;
	bign()//构造函数
	{
		this->len = 0;
		memset(d, 0, sizeof(d));
	}
};

当然，一般输入大整数时，都是先用字符串读入，然后再把字符串另存为至bign结构体。

bign change(const string str)//将整数转换为begin c语言用const char* 
{
	bign a;
	a.len = str.size();//bign的长度就是字符串的长度 c语言用strlen()函数
	for (int i = 0; i < a.len; i++)
	{
		a.d[i] = str[a.len - i - 1] - '0';
	}
	return a;
}

大整数的运算

对于大整数的四则运算，我们需要模拟在小学期间学习四则运算的思路和过程，也就是把我们在草稿纸上运算的过程，抽象成代码的逻辑。

1、高精度加法

加法实现方式与我们以前学到的加法一样。对于某一位的运算：我们将该位上的两个数字与进位相加，得到的结果取个位数作为该结果，十位数作为新的进位。

bign add(bign a, bign b)
{
	bign c;
	int carry = 0;	//carry是进位标志
	for (int i = 0; i < a.len || i < b.len; i++) //以较长的为界限 
	{
		int temp = a.d[i] + b.d[i] + carry;		//两个对应位与进位相加 
		c.d[c.len++] = temp % 10;		//取个位数为该位的结果 
		carry = temp / 10;	//取十位数为新的进位 
	}
	if (carry) //如果最后的进位不为0，则直接赋给结果的最高位  
	{
		c.d[c.len++] = carry;
	}
	return c;
}

这里要注意，这样写法的条件是两个对象都是非负整数。如果有双方异号，可以在转换到数组这一步时去掉符号，再使用高精度减法；如果双方都为负数，那么去掉负号后采用高精度加法，最后负号加回去即可。 

2、高精度减法

通过对减法步骤的拆分可以得到一个简练的步骤：对某一位，比较被减位和减位，如果不够减，则令被减位的高位减1，被减位加10再进行减法（借一位）；如果够减，那就直接减。最后需要注意减法后高位可能有多余的0，要去除它们，但要保证结果至少有一位数。

bign sub(bign a, bign b) //a - b
{
	bign c;
	for (int i = 0; i < a.len || i < b.len; i++) //以较长的为界限
	{
		if (a.d[i] < b.d[i]) //不够减 
		{
			a.d[i + 1]--;	//向高位借位 
			a.d[i] += 10; 	//向前位借10  
		}
		c.d[c.len++] = a.d[i] - b.d[i];		//减法结果为当前位 
	}
	while (c.len >= 2 && c.d[c.len - 1] == 0)    //剩余的位数不小于十位，并且最高位是0
	{
		c.len--;	//去除高位的0，同时至少保留一位最低位 
	}
	return c;
}

3、高精度乘以低精度

所谓高精度乘以低精度，就是bign*int的运算。

对某一位来说是这样的步骤：取bign的某位与int型整体相乘，再与进位相加，所得结果的个位数作为该结果，高位部分作为新的进位。对于a、b异号的情况只需要一个标志位变量记录，在输出的时候加上负号就行了。

bign multi(bign a, int b)
{
	bign c;
	int carry = 0;	//进位
	for (int i = 0; i < a.len; i++)
	{
		int temp = a.d[i] * b + carry;
		c.d[c.len++] = temp % 10;		//个位作为该结果
		carry = temp / 10;	//高位部分作为新的进位 
	}
 
	while (carry != 0) //和加法不一样，乘法的进位可能不止一位，因此用while 
	{
		c.d[c.len++] = carry % 10;
		carry /= 10;
	}
	return c;
}

4、高精度除以低精度

高精度除以低精度，就是bign/int的运算。考虑到有时还需要知道计算之后的余数，于是就把余数写成引用的形式传入，当然也可以把余数设成全局变量。 

对于某一位来说：上一步的余数乘以10加上该步的位，得到该步当前的被除数，将其与除数比较；如果不够除，则该位的商为0；如果够除，则商即为对应的商，余数即为对应的余数。和其他运算一样，要注意结果可能有多余的0，要去掉它们，但也要保证结果至少有一位数。

bign divide(bign a, int b, int& r) //r为余数 
{
	bign c;
	c.len = a.len;//被除数的每一位和商的每一位是一一对应的，因此先令长度相等 
	for (int i = a.len - 1; i >= 0; i--)  //从高位开始 
	{
		r = r * 10 + a.d[i];		//和上一位遗留的余数组合
		if (r < b) c.d[i] = 0;		//不够除，该位为0 
		else //够除 
		{
			c.d[i] = r / b;	//商
			r = r % b;		//获得新的余数 
		}
	}
	while (c.len >= 2 && c.d[c.len - 1] == 0)
	{
		c.len--; //去除高位的0，同时至少保留一位最低位 
	}
	return c;
}

如果大家对于上述的逻辑还不清楚的话，可以自己在稿纸上举例几个简单的数算算，实际思路和我们运算时的思路是一样的哈。

大整数的表示

最后，当我们要打印出大整数时则要注意了，在上文中，我们为了方便运算，将数组中的位序翻转了一次，所以打印时就是需要从后往前输出。

而如果我们输入的数据是【04】，那么输出的结果就不是单纯的【4】了，一般来说这不是我们想要的结果是吧。那么为了解决这个问题，我们可以在打印的时候加上一个标志位来判断。

void print(bign ans)
{
	int flag = 0;
	for (int i = ans.len - 1; i >= 0; i--)
	{
		if (ans.d[i] != 0)    //标志位如果首位是0 则不输出
		{
			flag = 1;
		}
		if (flag)
		{
			cout << ans.d[i];
		}
	}
	if (!flag)
		cout << 0;    //包含输出0的情况
}