-
Vatti clipping 算法介绍
一、背景
Vatti clipping 算法是很多几何图形库的底层实现原理, 比如clipper2就是基于Vatti clipping算法来实现的,本文介绍Vatti clipping算法中的基本概念以及其算法原理。
二、基本概念
下面是Vatti clipping算法中的基本概念:
1. 点(Vertex)
由于double在计算机中表示的精度问题,一般的几何图形库支持的基本数据类型都是整型数值类型(clipper2中虽然带有支持double类型的接口,其实现也是接收用户输入的double类型,转为integer类型后再进行计算,计算完成后,转为double类型返回给用户),点的数据结构为:
struct Vertex { int64_t x; int64_t y; };- 1
- 2
- 3
- 4
2. 点的顺序(Vertex order)
Vatti 算法中通常优先按照y值进行对点排序,如果y值相等,则按照x值进行排序,点的比较算法为:
bool operator<(const Vertex& a, const Vertex& b) { if (a.y == b.y) { return a.x < b.x; } return a.y < b.y; }- 1
- 2
- 3
- 4
- 5
- 6
3. 边 (Edge)
一条边e由两个点组成: start和end,边的起点和终点满足: e.start < e.end,边的数据结构为:
struct Edge { Vertex start; Vertex end; };- 1
- 2
- 3
- 4
3.1 左侧边和右侧边(Left-hand Edge and Right-hand Edge)
左和右是相对于图形的内侧区域而言的,在图形内侧的左边的边称为左侧边,在图形内侧的右边的边称为右侧边。如下图1

图1 (图片来源:Computer graphics and geometric modeling: implementation and algorithms ) 图1中:
- Left edges: p 0 p 8 , p 8 p 7 , p 7 p 6 p_0p_8, p_8p_7, p_7p_6 p0p8,p8p7,p7p6, 和 p 4 p 3 , p 3 p 2 p_4p_3, p_3p_2 p4p3,p3p2
- Right edges: p 0 p 1 , p 1 p 2 p_0p_1, p_1p_2 p0p1,p1p2, 和 p 4 p 5 , p 5 p 6 p_4p_5, p_5p_6 p4p5,p5p6
3.2 左侧界和右侧界 (Left Bounds and Right Bounds)
连续的左侧边组成一个左侧界,连续的右侧边组成一个右侧界。上图1中:
- Left Bounds:
- B 1 = ( p 0 p 8 , p 8 p 7 , p 7 p 6 ) B_1 = (p_0p_8, p_8p_7, p_7p_6) B1=(p0p8,p8p7,p7p6)
- B 2 = ( p 4 p 3 , p 3 p 2 ) B_2 = (p_4p_3, p_3p_2) B2=(p4p3,p3p2)
- Right Bounds:
- B 3 = ( p 0 p 1 , p 1 p 2 ) B_3 =(p_0p_1, p_1p_2) B3=(p0p1,p1p2)
- B 4 = ( p 4 p 5 , p 5 p 6 ) B_4 = (p_4p_5, p_5p_6) B4=(p4p5,p5p6)
4. 局部最小多边形(Local mininum)
一个局部最小多边形(Local minimum)由一个根节点(root vertex),以及其相连的左侧界和右侧界组成,这些左侧界和右侧界同时必须满足以下条件:
- 左侧界和右侧界的第一条边不能是水平的
- 左侧界和右侧界的最后一条边不能是水平的
如下图2所示,黑色部分是根节点,绿色部分是左侧界,红色部分为右侧界,下面的多边形可以由三个黄色虚线框标出的Local mininum组成。
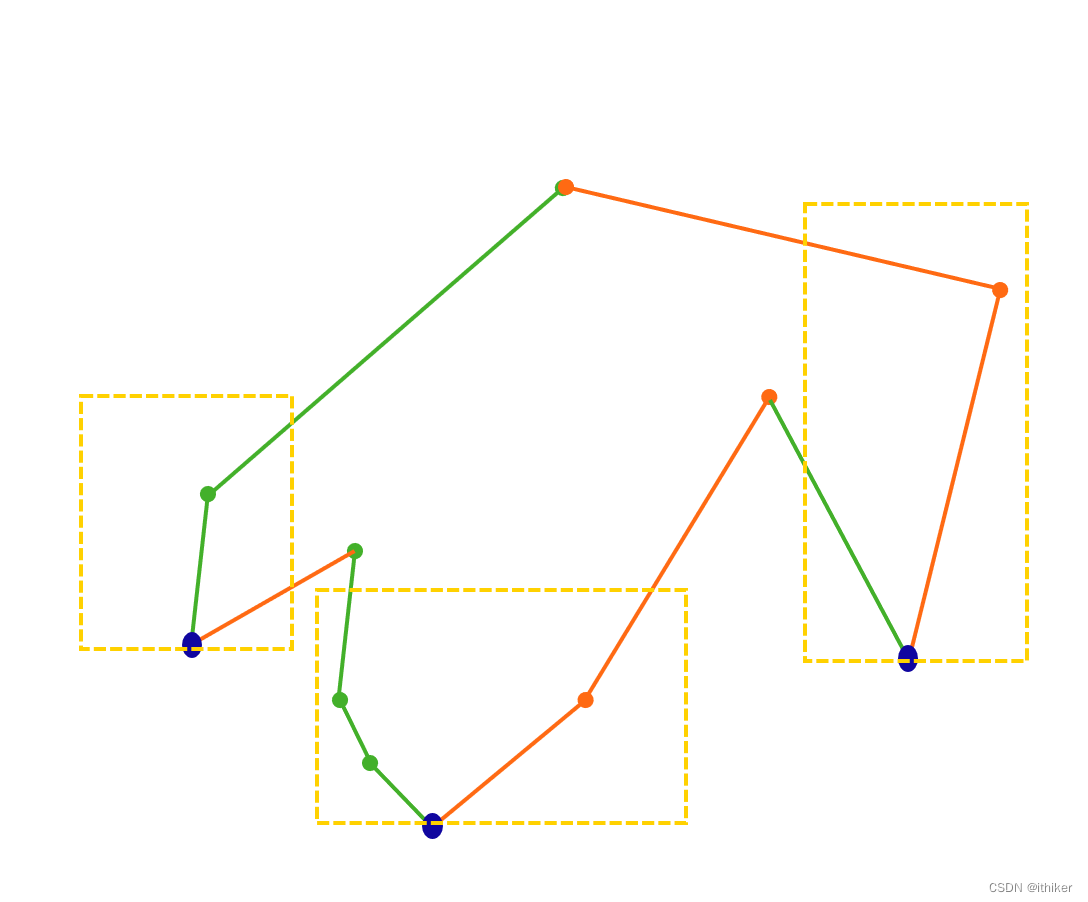
图2 5. 局部最小多边形集(Local Mininum List: LML)
将图2中的三个黄色虚线框标出的最小多边形放到一个集合中,并按黑色根节点的y坐标按照从小到大排序,就得到了Local mininum的集合,即LML。
6. 扫描线(Scan Line)
从下往上,经过多边形的每一个顶点以及多边形边的交点的水平直线,称为扫描线。
对于LM,如果它的根节点位于Scan Line上,那么,该LM起始于该Scan Line。7. 活跃边(Active edge)
如果某条非水平的边和Scan Line相交(包含边的起点,终点在Scan Line上,或者边的中间部分和Scan Line相交),那么称这条边为活跃边(Active edge)。根据交点在Active edge上的不同位置:
- 如果交点是Active edge的起点,那么称该Active edge位于Scan Line之上
- 如果交点是Active edge的终点,那么称该Active edge位于Scan Line之下
- 如果交点是Active edge除掉起点和终点的其它点,那么称该Active edge位于Scan Line之下或之上
如下图3,红色的Active edge位于Scan Line之上,蓝色的Active edge位于Scan Line之下,黑色的Active edge位于Scan Line之下或之上:
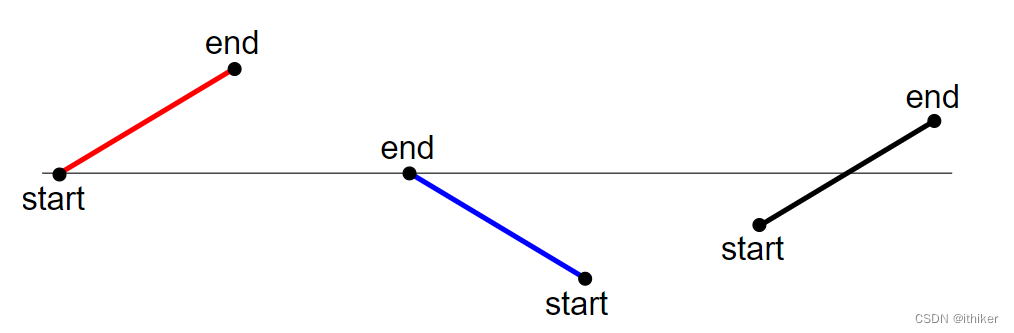
图3:Active edge和Scan Line的关系 1. 对Active edge进行排序
如果Active edge位于Scan Line之上(包含相交),这些Active edges将按照交点(与Scan Line 相交)或起点(位于Scan Line之上)的X坐标值进行排序,如果坐标值相等,将按顺时针方向对这些Active edge进行排序,如下图4,位于Scan Line之上或相交的红色Active edges的排序如标号所示:
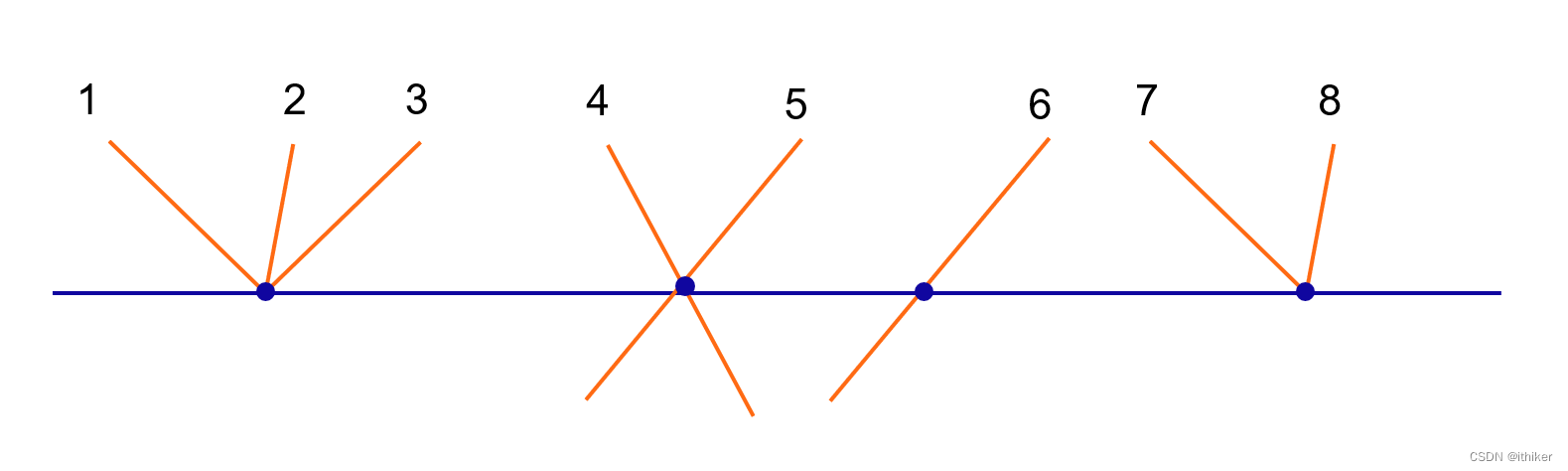
图4:位于Scan Line之上的Active edge的排序 如果Active edge位于Scan Line之下(包含相交),这些Active edges将按照交点(与Scan Line 相交)或终点(位于Scan Line之上)的X坐标值进行排序,如果坐标值相等,将按逆时针方向对这些Active edge进行排序,如下图5,位于Scan Line之下或相交的绿色Active edges的排序如标号所示:
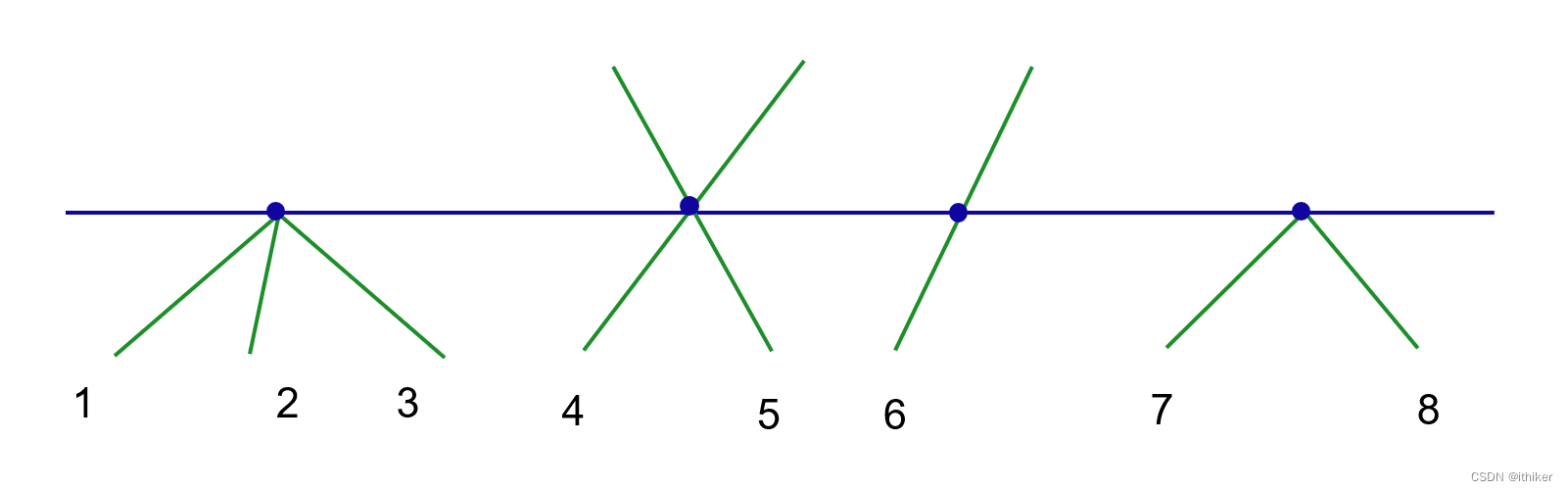
图5:位于Scan Line之下的Active edge的排序。 共线的Active edge可以随意排序。 三、算法介绍
Vatti clipping的核心算法分为以下几步:
- 生成图形的LML
- 根据LML的root vertex,生成一个Scan Beam List(SBL), SBL里面是按从小到大排好序的root vertex的Y坐标值
- 从SBL中取出最小的Y值,找到和纵坐标值为Y的Scan line相交的所有活跃边(Active edges)
- 处理找到的Active edges
- 将每条Active edge的终点的Y坐标加入到SBL, 并将SBL维持在有序状态
- 找出和当前Scan line相交的边的交点以及从SBL中获得的Y坐标生成的下一条Scan Line相交的交点
- 处理这些位于Scan beam内部的交点(不含Scan beam上部的交点)
- 将Scan Line移动到Scan beam上部,找到对应的Active edges
- 重复4-9步骤直到所有的图形都处理到了
下面详细介绍各步:
1. 生成图形的LML
LML是根据vertex排好序了的,排序规则是根据root vertex按照点的排序规则进行排序。对于root vertex重合的情况,顺序可以是任意的。
2. 初始化SBL
SBL里面是按从小到大排好序的LML的所有root vertex的Y坐标值
3. 生成Scan Line
取出并删除SBL中的最小值,形成一条Scan Line
4. 找到Active Edges
找到和当前Scan Line相交的所有活跃边:
- 找到位于Scan Line之下的Active Edges
那些和上一条Scan Line相交的边或者起点和上一条Scan Line重合的边,是位于当前Scan Line之下的边。如下图6所示:
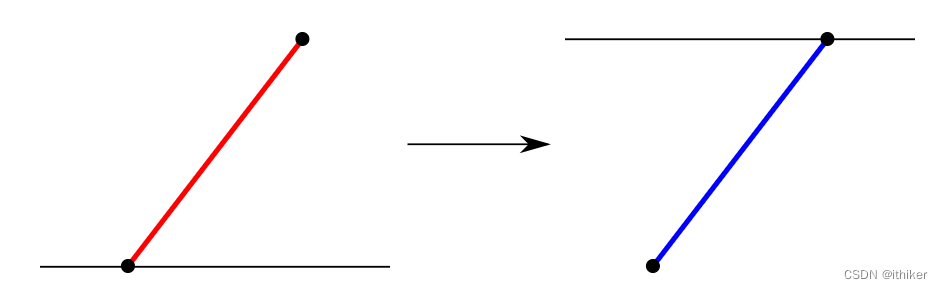
图6 - 找到位于Scan Line之上的Active Edges
- 和上一条Scan Line相交的边或者起点和上一条Scan Line重合且终点不和当前Scan Line重合的边,是位于当前Scan Line之上的Active Edges,如下图7所示:
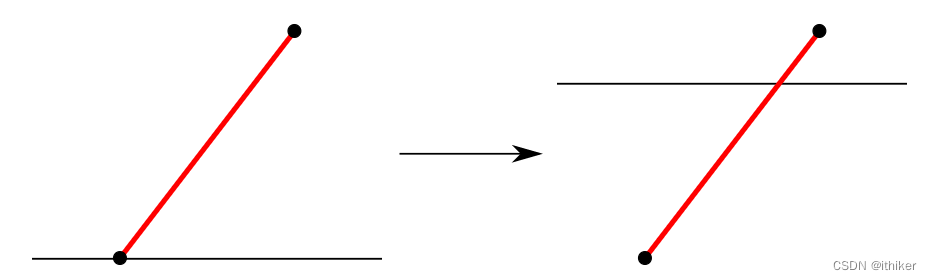
图7 - 和上一条Scan Line相交的边或者起点和上一条Scan Line重合且终点和当前Scan Line重合的边,以及起点位于当前Scan Line的边,是位于当前Scan Line之上的Active Edges,如下图8所示:
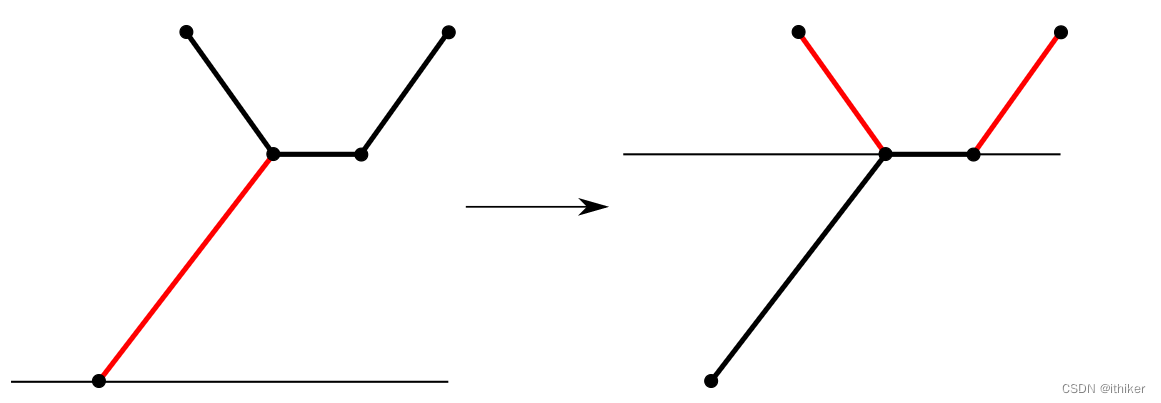
图8 - 对与LM,如果其root verter和当前Scan Line重合,那么它的第一条左侧边(Left edge)和第一条右侧边(Right edge),是位于当前Scan Line之上的Active Edges,如下图9所示:

图9 这里对于水平边(Horizontal edges)和共线边(Collinear edges)的处理要注意:
- Active Edges中是没有水平边的,对于这些和Scan Line重合的水平边,放在一个闭区间的集合中。和Active Edges分开存放
- 对于共线的Active Edges, 这在Vatti clipping算法是必须要通过其它办法修正的:
- 如果对于Scan line上方的两条active edge是colinear的,那么比较长的那条边将会被分成两部分:和其它active edge重合的部分将会被移除,剩下的部分和图形的其它部分向连接。
- 如果两条colinear的active edge完全重合,那么,其中一条将会被移除,之前和被移除的active edge相连接的边和剩下没有被移除的active edge相连接。
对于共线的Active Edges的处理示意图如下图10所示:
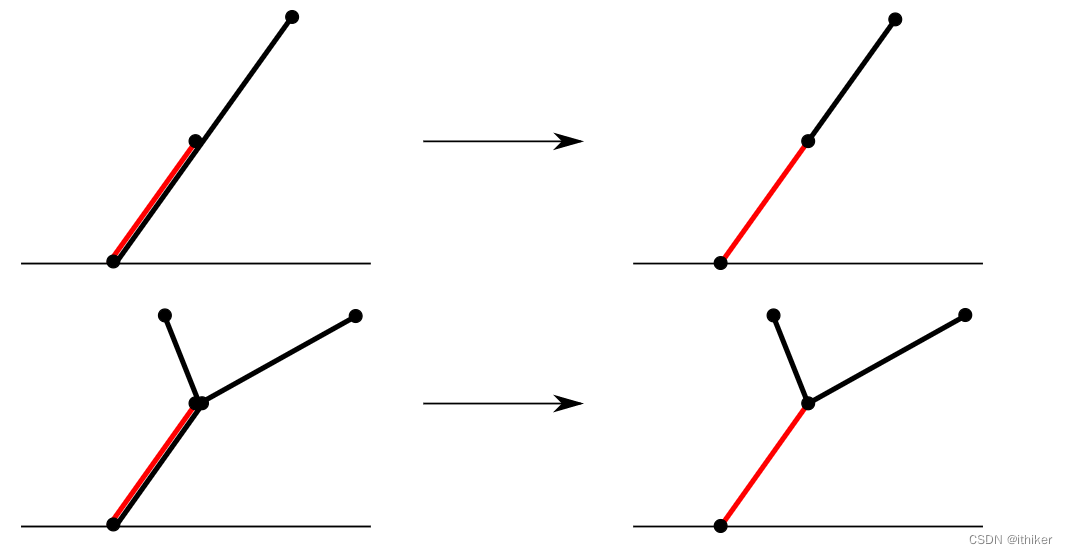
图10 5. 处理active edges
对于每条Active edge, 记x为下面的任意一种情况的X坐标的值:
- 如果Active edge和Scan Line相交,交点的X坐标的值
- 如果Active edge的起点和Scan Line重合,起点的X坐标的值
- 如果Active edge的终点和Scan Line重合,终点的X坐标的值
这样,每条active edge都对应于一个x值,对于还未处理的active edges集合,则由一个x值的集合,找到最小的x值。对于下图10中:
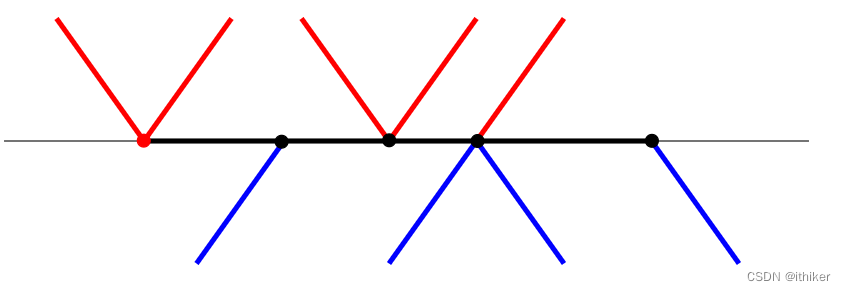
图10 上图中标红的点是最小的x值对应的点,Scan Line上方的active edges是红色的,Scan Line下方的active edges是蓝色的,水平边是黑色的。
对和红点相连的active edges的进行如下处理(如适用才处理):
- 将Right-hand Edge上的vertex添加到左侧的polygon, 如下图11所示:
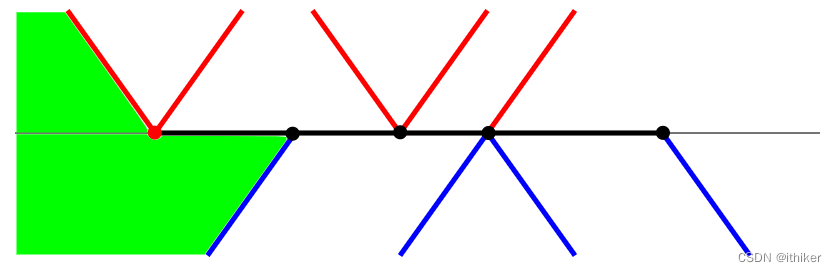
图11 - 在Scan Line下方的Active edge的终点叫做top vertices,将它们添加到Scan Line下方的polygon, 如下图12所示:
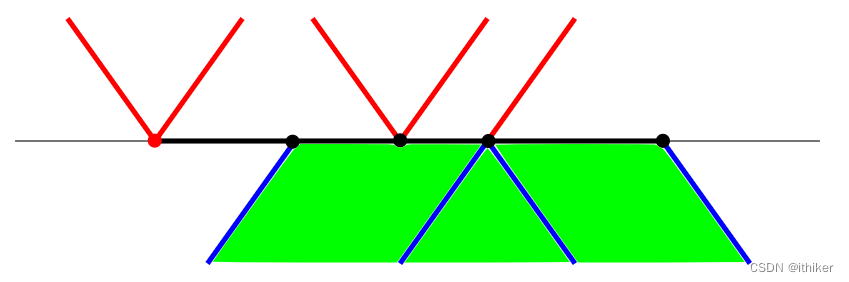
图12 - 在Scan Line上方的Active edge的起点叫做bottom vertices,将它们添加到Scan Line上方的polygon, 如下图13所示:
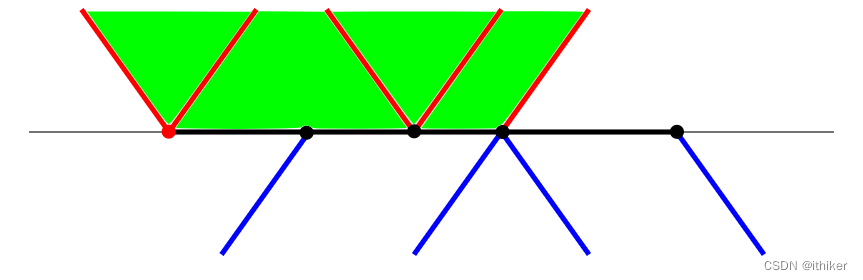
图13 - 将Left-hand Edge上的vertex添加到右侧的polygon, 如下图14所示:
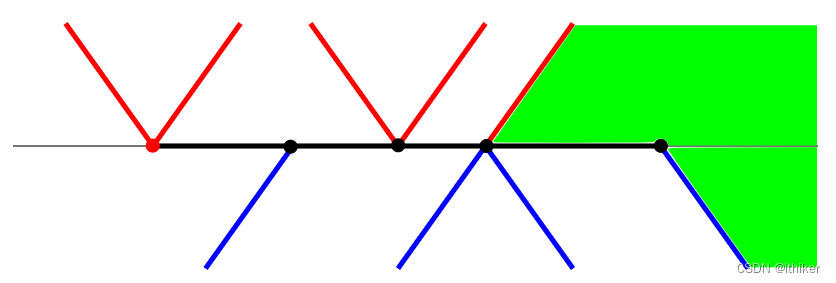
图14 接下来,对没有处理的active edges, 重复上面的步骤直到所有的active edges都处理完毕。
上面的处理过程中,有两种特殊情况需要进行特殊处理:- 如果Scan Line下方没有active edges,那么左侧的polygon必须拆分成两个,如下图15虚线所示:

图15 - 如果Scan Line上方没有active edges,那么左侧的polygon和右侧的polygon必须合并成1个,如下图16虚线所示:
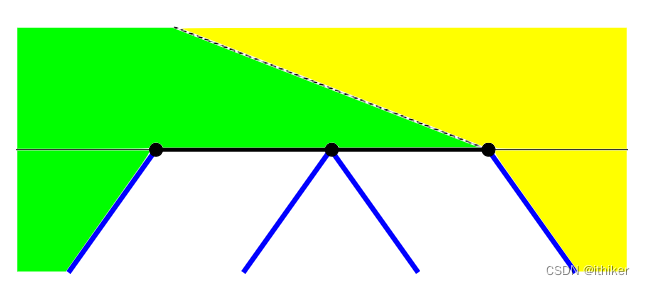
图16 这里图15和图16分别对应的是Scan Line位于要处理的图形的最底部和最顶部的情况。
未完待续
Reference:
-
相关阅读:
Vue条件渲染和列表渲染
软考 系统架构设计师系列知识点之基于架构的软件开发方法ABSD(1)
引用类型详解
好用的在线思维导图软件--GitMind
设计模式之代理模式的懂静态代理和动态代理
利用人工智能做射击游戏辅助(一)AlphaPose简介
毕业论文中的数据分析无从下手?
学生Dreamweaver静态网页设计 基于HTML+CSS+JavaScript制作简食餐厅美食网站制作
pyinstaller打包完整python项目
ES6 入门教程 10 对象的扩展 10.7 AggregateError 错误对象 & 10.8 Error 对象的 cause 属性
- 原文地址:https://blog.csdn.net/gigglesun/article/details/127712621