vision transformer的位置编码总结

绝对位置编码

Vit采用绝对位置编码的形式，也就是使用一个值来表征每个patch的绝对位置，并且基于可学习的方式，一般的定义方式为：

absolute_pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dim))
trunc_normal_(absolute_pos_embed, std=.02)
1
2

将得到的position encoding直接加到输入的patch embedding就可以了：

x = x + self.absolute_pos_embed
1

相对位置编码

Swin transformer中采用了相对位置编码的概念，考虑query和key的相对位置进行编码。
具体的详解参考：https://blog.csdn.net/qq_37541097/article/details/121119988

这里的Relative Position Bias是加到self-attention的similarity矩阵计算的时候，而不是patch embedding，且在每层的self-attention计算时候都使用，具体的公式为：

$\mathrm{Attention}(Q,K,V)=\mathrm{SoftMax}(\frac{Q{K}^T}{\sqrt{d}}+B)V$

这里$B$是Relative Position Bias。如下图，假设输入的feature map高宽都为2，那么首先我们可以构建出每个像素的绝对位置（左下方的矩阵），对于每个像素的绝对位置是使用行号和列号表示的。比如蓝色的像素对应的是第0行第0列所以绝对位置索引是( 0 , 0 ) (0,0)(0,0)，接下来再看看相对位置索引。首先看下蓝色的像素，在蓝色像素使用q与所有像素k进行匹配过程中，是以蓝色像素为参考点。然后用蓝色像素的绝对位置索引与其他位置索引进行相减，就得到其他位置相对蓝色像素的相对位置索引。例如黄色像素的绝对位置索引是( 0 , 1 ) (0,1)(0,1)，则它相对蓝色像素的相对位置索引为( 0 , 0 ) − ( 0 , 1 ) = ( 0 , − 1 ) (0, 0) - (0, 1)=(0, -1)(0,0)−(0,1)=(0,−1)，这里是严格按照源码中来讲的，请不要杠。那么同理可以得到其他位置相对蓝色像素的相对位置索引矩阵。同样，也能得到相对黄色，红色以及绿色像素的相对位置索引矩阵。接下来将每个相对位置索引矩阵按行展平，并拼接在一起可以得到下面的4x4矩阵 。

实现代码如下：

>>> coords_h = torch.arange(2)
>>> coords_w = torch.arange(2)
>>> coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
>>> coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
>>> coords_flatten
tensor([[0, 0, 1, 1],
        [0, 1, 0, 1]])
>>> relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
>>> relative_coords
tensor([[[ 0,  0, -1, -1],
         [ 0,  0, -1, -1],
         [ 1,  1,  0,  0],
         [ 1,  1,  0,  0]],

        [[ 0, -1,  0, -1],
         [ 1,  0,  1,  0],
         [ 0, -1,  0, -1],
         [ 1,  0,  1,  0]]])
>>> relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

请注意，我这里描述的一直是相对位置索引，并不是相对位置偏执参数。因为后面我们会根据相对位置索引去取对应的参数。比如说黄色像素是在蓝色像素的右边，所以相对蓝色像素的相对位置索引为( 0 , − 1 ) (0, -1)(0,−1)。绿色像素是在红色像素的右边，所以相对红色像素的相对位置索引为( 0 , − 1 ) (0, -1)(0,−1)。可以发现这两者的相对位置索引都是( 0 , − 1 ) (0, -1)(0,−1)，所以他们使用的相对位置偏执参数都是一样的。但在源码中作者为了方便把二维索引给转成了一维索引。由于索引的值范围为$[-M+1,M-1]$,原始的相对位置索引上加上$M-1$，使得索引的值大于等于0，变为$[0,2M-2]$。

接着将所有的横坐标标都乘上$2M-1$,方便之后横坐标和纵坐标求和之后的索引的独一性。

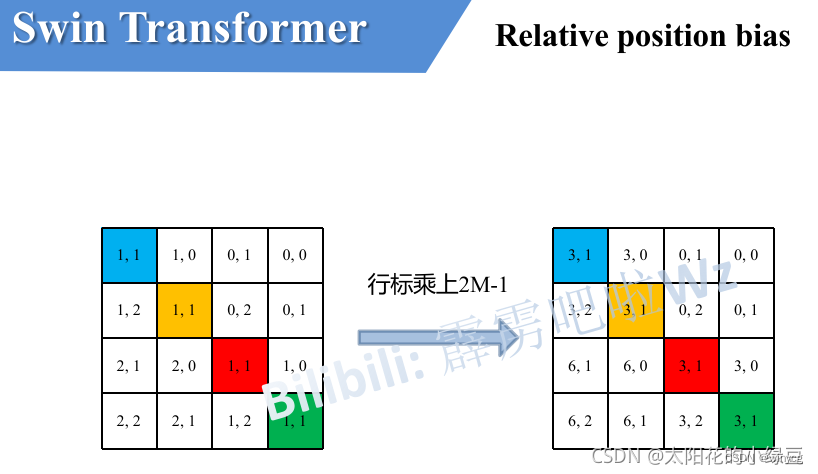
最后将行标和列标进行相加，得到独一的一维的索引。

>>> M=2
>>> relative_coords[:, :, 0] += M - 1
>>> relative_coords[:, :, 1] += M - 1
>>> relative_coords[:, :, 0] *= 2 * M - 1
>>> relative_position_index = relative_coords.sum(-1)
>>> relative_position_index
tensor([[4, 3, 1, 0],
        [5, 4, 2, 1],
        [7, 6, 4, 3],
        [8, 7, 5, 4]])
1
2
3
4
5
6
7
8
9
10

之前计算的是相对位置索引，并不是相对位置偏执参数。真正使用到的可训练参数
是保存在relative position bias table表里的，这个表的长度是等于$(2M-1)\times (2M-1)$的。那么上述公式中的相对位置偏执参数B是根据上面的相对位置索引表根据查relative position bias table表得到的，如下图所示。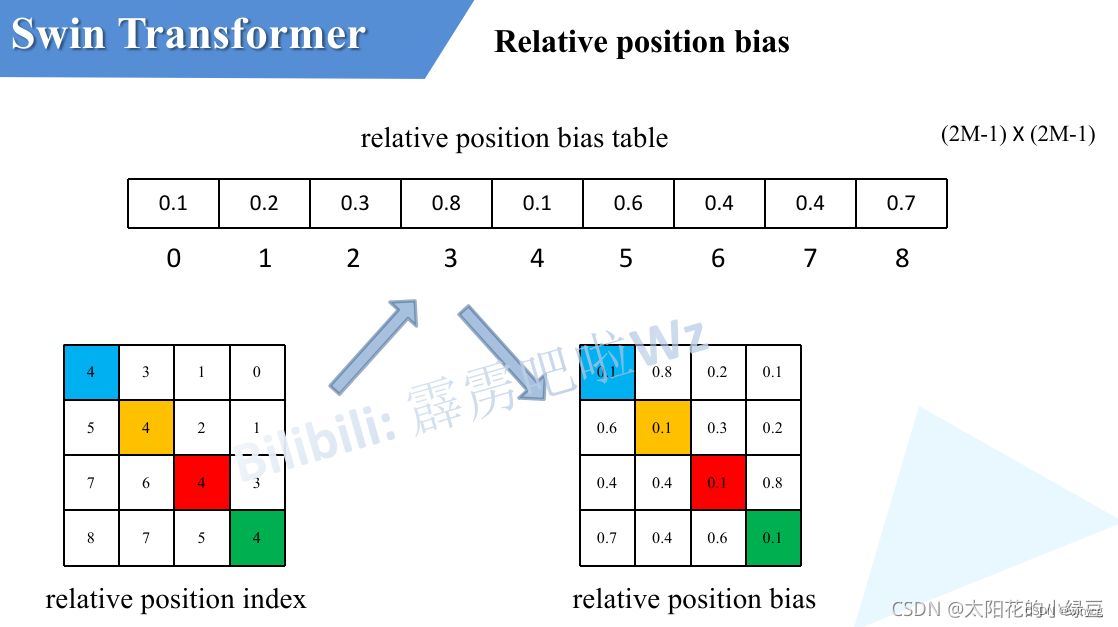

Swin transformer的ablation study：

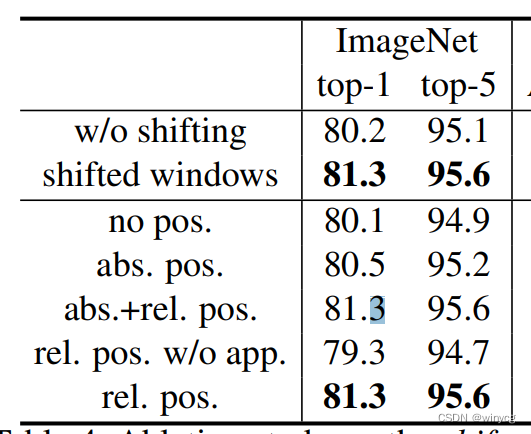
绝对编码 （absoluate position）能提升性能，但是效果不如相对编码（relative position），仅仅是相对编码的效果等价于相对编码+绝对编码