Leftover Hash Lemma(LHL):剩余哈希引理

Leftover Hash Lemma(LHL):剩余哈希引理

目录

一. 抗碰撞哈希函数

二. Universal 哈希函数

三.剩余哈希引理

四.广义的剩余哈希引理

哈希函数是一种确定多项式时间可计算的函数。在不同的应用场景中，对哈希函数的性质要求是不同的。本篇文章将首先解释两种常用的哈希函数，接着阐述剩余哈希引理（Leftover Hash Lemma）的理解。

一. 抗碰撞哈希函数

一个哈希函数族 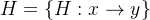$H=\lbrace H:x\rightarrow y\rbrace$ 是抗碰撞的，如果对于任意的PPT敌手 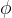$\phi$ ，满足如下方程：

$Adv_{H,\phi}^{cr}(n):=Pr[H,(x,x')\leftarrow \phi(H):H(x)=H(x')\wedge x\not= x']\leq negl(n)$

二. Universal 哈希函数

一个哈希函数族 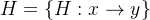$H=\lbrace H:x\rightarrow y\rbrace$ 是universal的，如果对于所有 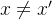$x\not= x'$ ，都有如下：

$Pr[H:H(x)=H(x')]\leq \frac{1}{|y|}$

三.剩余哈希引理

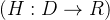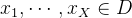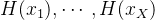剩余哈希引理主要是针对Universal哈希函数。一个哈希函数族 $(H:D\rightarrow R)$ 被称之为X-wise独立的，如果对于任意X个元素 $x_1,\cdots,x_X\in D$ ,变量 $H(x_1),\cdots,H(x_X)$ 是均匀随机的。

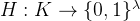令 $H:K\rightarrow \lbrace 0,1\rbrace^\lambda$ 是一个2-wise独立的哈希函数族。令 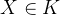$X\in K$ 是一个随机变量且满足 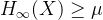$H_\infty(X)\geq\mu$ ，则有如下：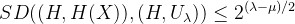

$SD((H,H(X)),(H,U_\lambda))\leq 2^{(\lambda-\mu)/2}$

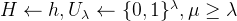
上式子中， $H\leftarrow h, U_\lambda\leftarrow \lbrace 0,1\rbrace^\lambda,\mu\geq\lambda$

四.广义的剩余哈希引理

令 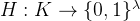$H:K\rightarrow \lbrace 0,1\rbrace^\lambda$ 是一个4-wise独立的哈希函数族。令 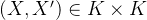$(X,X')\in K\times K$ 是两个随机变量且满足如下：

$H_\infty(X)\geq \mu,\quad H_\infty(X')\geq \mu,\quad Pr[X=X']\leq\delta$

则可得到如下：

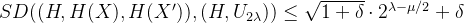
$SD((H,H(X),H(X')),(H,U_{2\lambda}))\leq \sqrt{1+\delta}\cdot 2^{\lambda-\mu/2}+\delta$

上式子中， $H\leftarrow h, U_{2\lambda}\leftarrow \lbrace 0,1\rbrace^{2\lambda}$

给出如上完整的定义，比较通俗的理解方式后续再补充。
相关阅读:
NodeJs原理 - Stream(二)
从IO谈论编程的基础
 使用SpringBoot将图片上传至阿里云OSS
戴尔G3-3579改固态散热
 c++小学生入门课程（一）
【原创】非常详细！VMware安装Rocky Linux服务器系统并执行优化，包括修改安装镜像源、ssh免密等等
 关系型数据库的问题和NoSQL数据库的应用
 python正则表达式实战——获取图片
 四十九.强化学习基础
 ASPNetZero 11.4 Release Angular + MVC + Crack
原文地址：https://blog.csdn.net/forest_LL/article/details/127706216

一. 抗碰撞哈希函数

二. Universal 哈希函数

三.剩余哈希引理

四.广义的剩余哈希引理