快速排序Java

我们先看图~

换一个例子 

 

 

 

没错
这个流程图,
就是快排的思想
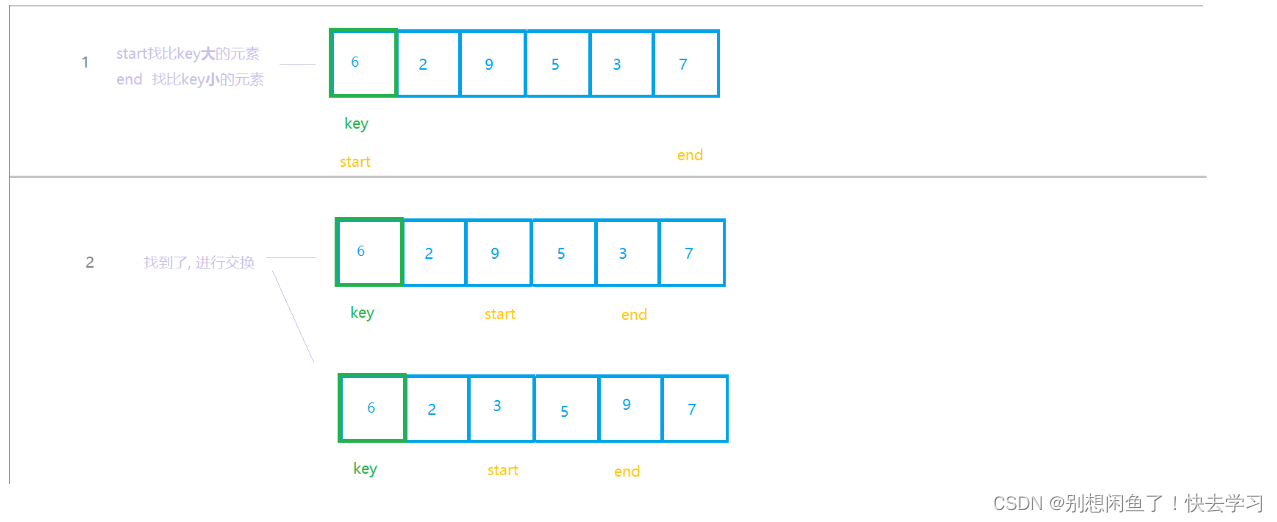
我们把第一个数, 成为key
start寻找比它大的数
end寻找比它小的数
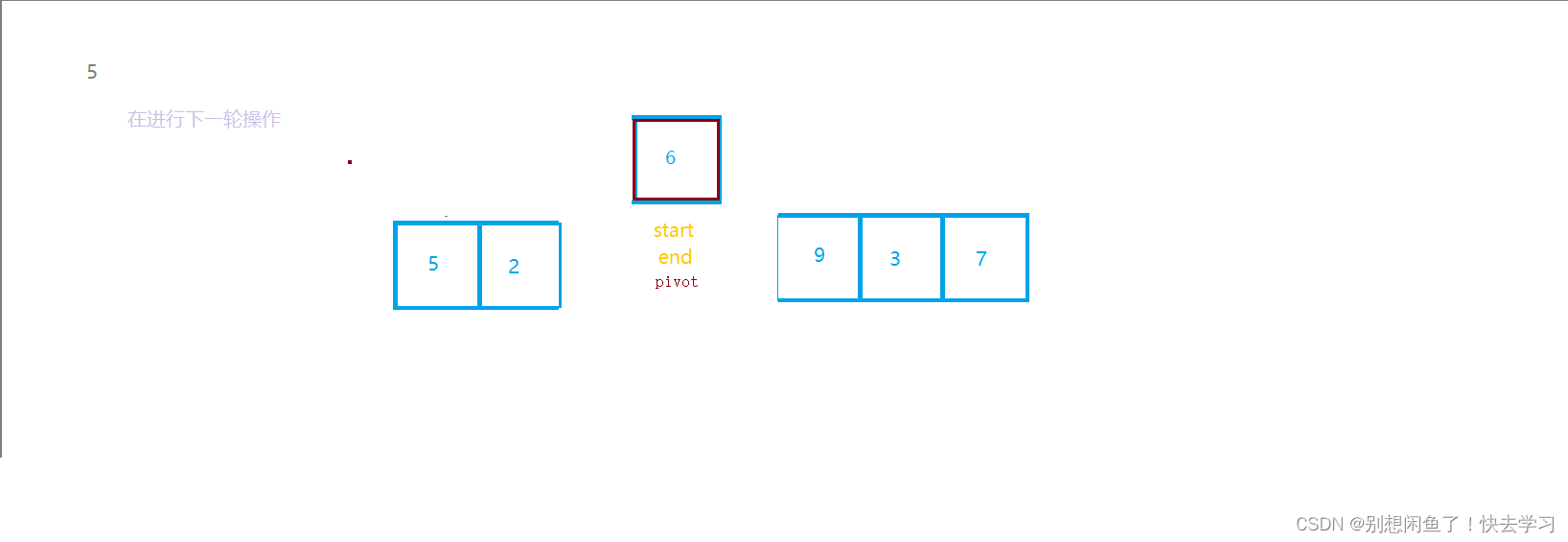
之后, start与end 进行交换
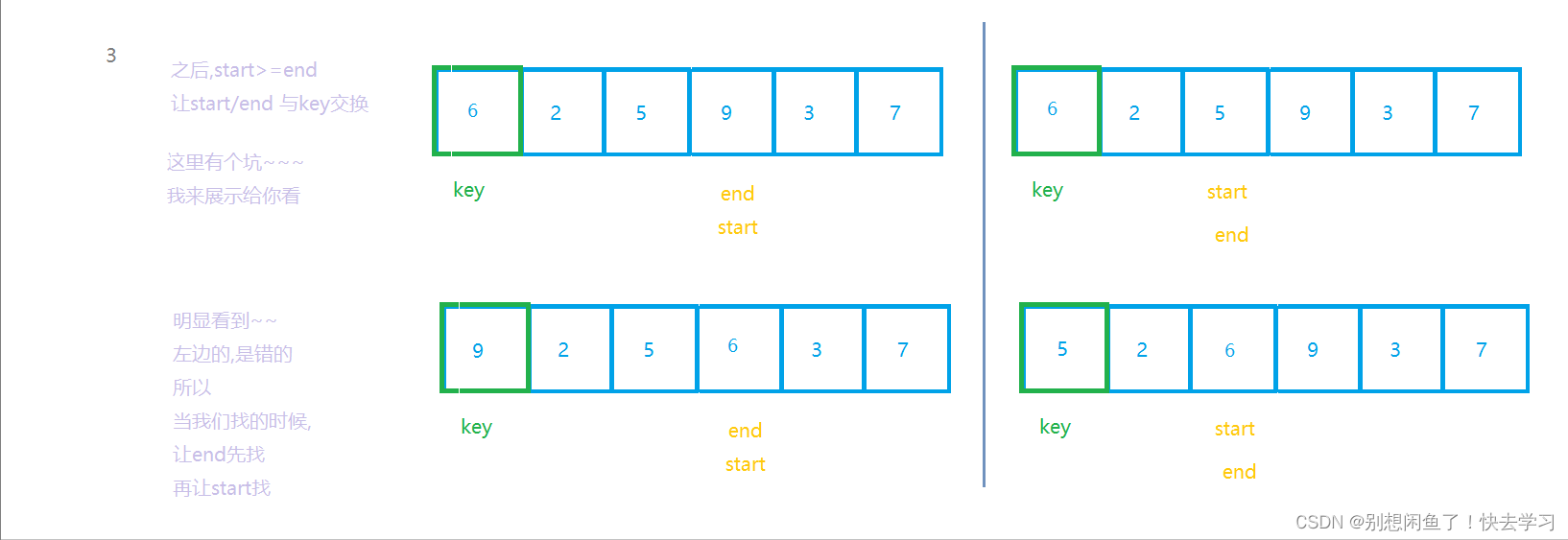
当start>=end, 我们再将 start>=end的位置下标作为下一轮的end,与start

这是hoare法

okk.去写代码吧~~

哎哎哎,但是记得回来~~~ 这种方法,时间复杂度有点高!!!我们要改进一下

import java.util.Arrays;
 
 
public class Main {
 
    public static void main(String[] args) {
        int[] arr = {6,2,9,5,3,7};
        quickSort(arr);
        System.out.println(Arrays.toString(arr));
    }
 
    private static void quickSort(int[] arr) {
        quick(arr,0,arr.length-1);
    }
 
    // 分段
    private static void quick(int[] arr, int left, int right) {
 
        if(left>=right){
            return;
        }
        // pivot是基准
        int pivot = partition(arr,left,right);
        quick(arr,left,pivot-1);
        quick(arr,pivot+1,right);
    }
 
    // 排序
    private static int partition(int[] arr, int start, int end) {
        int i = start;
        int key = arr[start];
        while (start<end) {
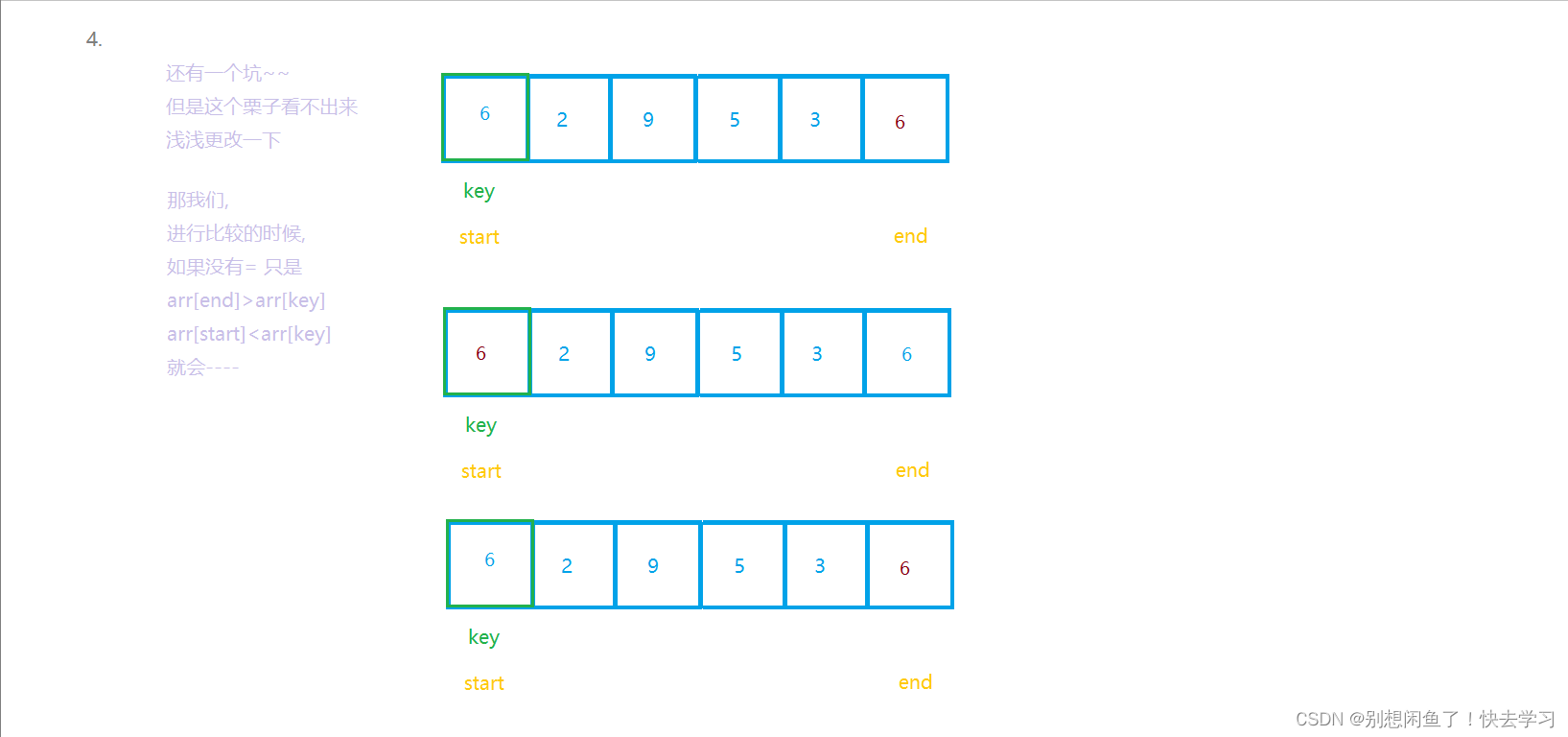
            // key<=arr[end] 要取= 不然会死循环
            while (start<end && key<=arr[end]) {
                end--;
            }
            // key<=arr[end] 要取= 不然会死循环
            while (start<end && key>=arr[start]){
                start++;
            }
            swap(arr,start,end);
        }
        swap(arr,i,start);
        return start;
    }
 
    private static void swap(int[] arr, int start, int end) {
        int tmp = arr[start];
        arr[start] = arr[end];
        arr[end] = tmp;
    }
 
 
}

 okk,我们现在说说有关时间复杂度的问题

在理想情况下,每次都是均分待排序序列 时间复杂度 O(N*logN)
在数组有序或者逆序时, 最慢 O(n^2)
(并且数据太多,递归太深,还会栈溢出)
给你康康图,这里带你推导,这个数是怎么产生的了~~~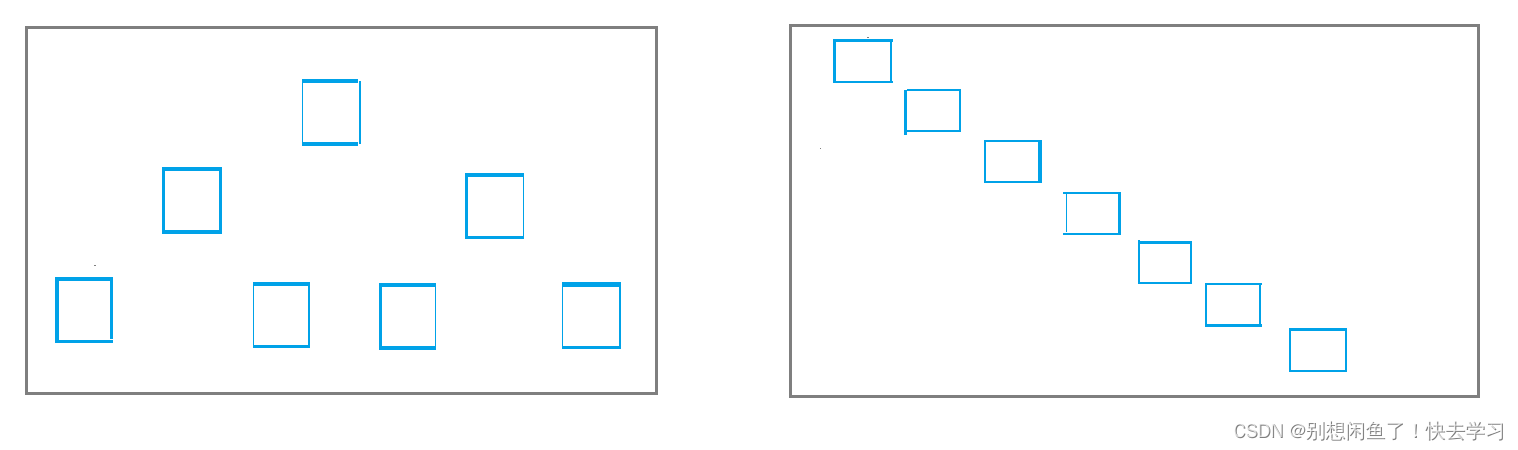

 所以,一般情况下,快排使用场景---无序
但是针对有序情况下我们还要进行处理,优化一下~~~

比如--随机选取基准法--三数取中法

介绍一下挖坑法

我们还是先看图

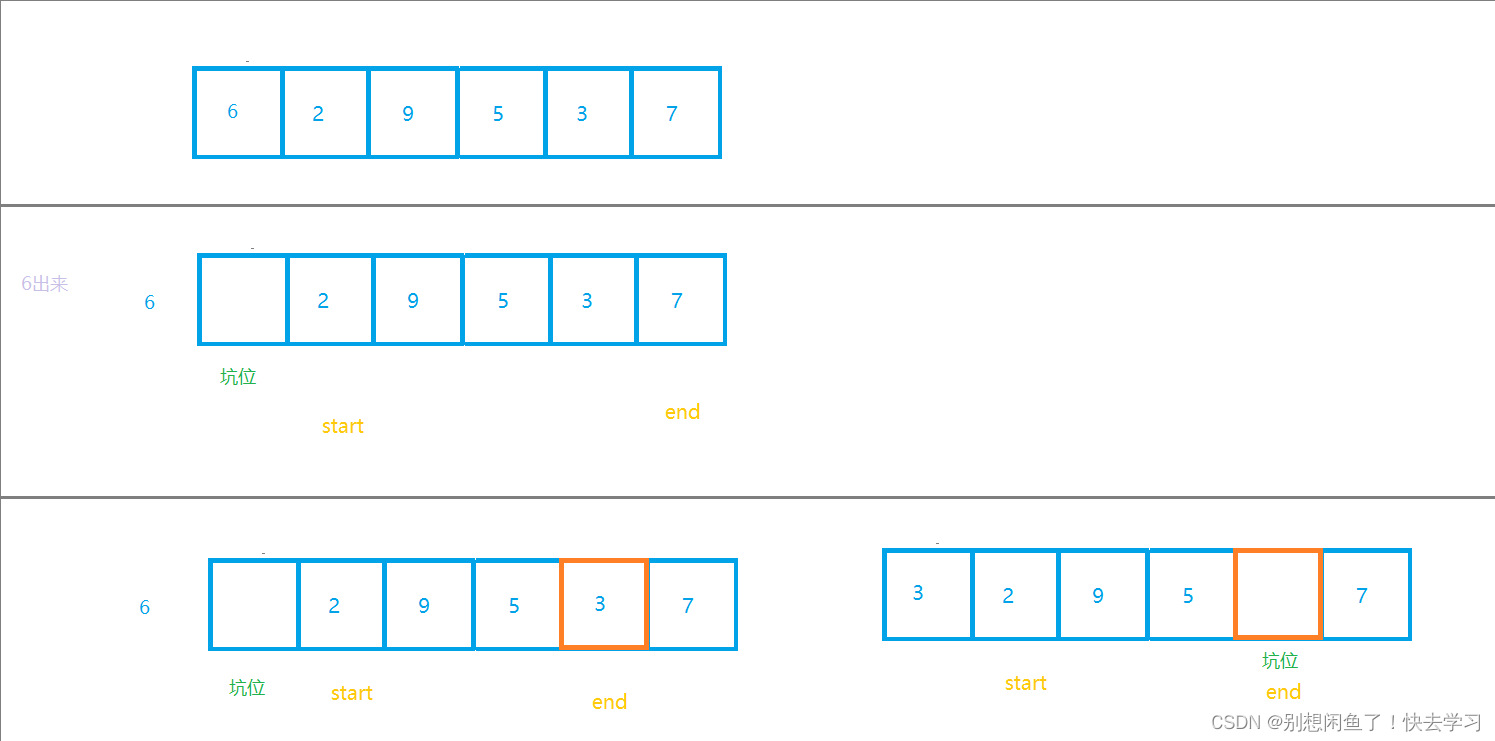
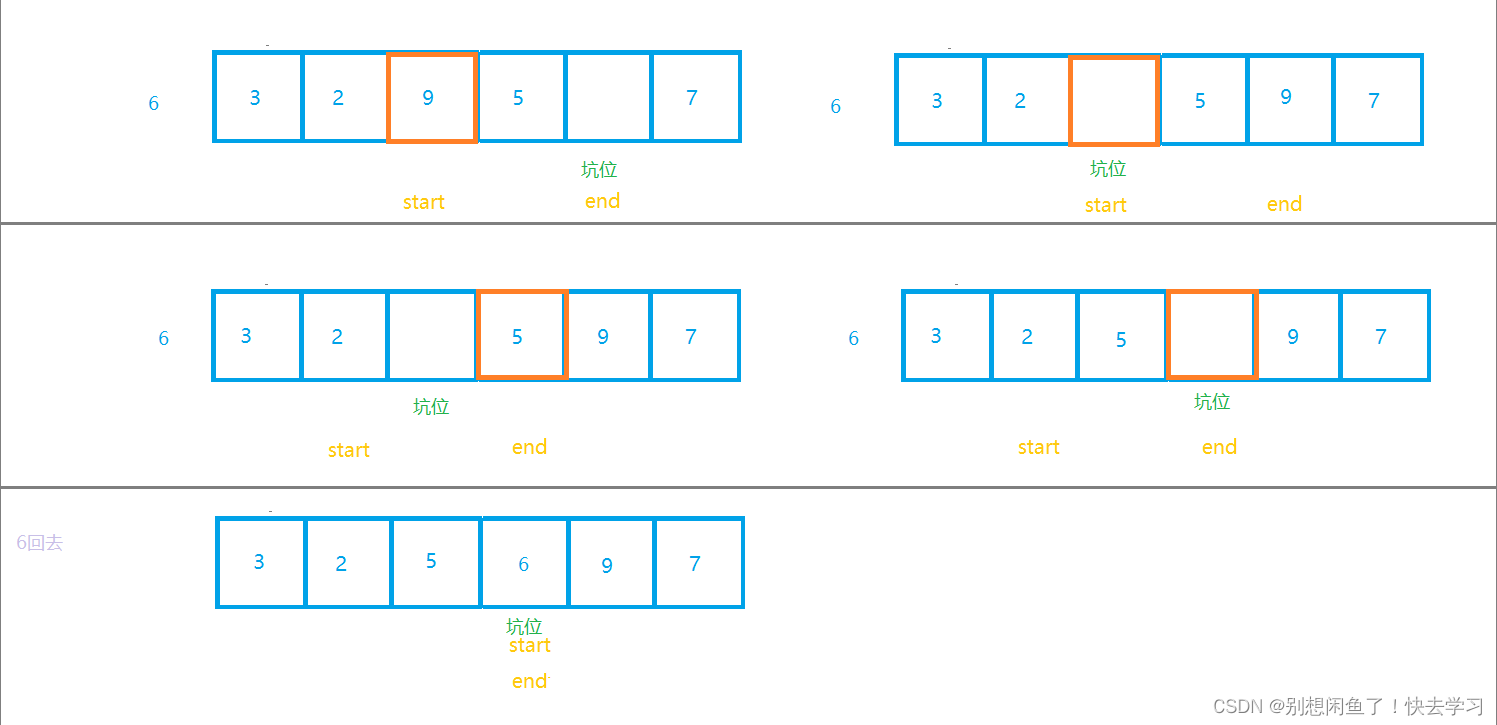
okk, 这就可以根据图, 来写代码了~~~

import java.util.Arrays;
 
public class Hole {
    public static void main(String[] args) {
        int[] arr = {4,2,9,5,3,7};
        quickSort(arr);
        System.out.println(Arrays.toString(arr));
    }
 
    private static void quickSort(int[] arr) {
        quick(arr,0,arr.length-1);
    }
 
    // 分段
    private static void quick(int[] arr, int left, int right) {
 
        if(left>=right){
            return;
        }
        // pivot是基准
        int pivot = partitionHole(arr,left,right);
        quick(arr,left,pivot-1);
        quick(arr,pivot+1,right);
    }
 
    // 排序
    private static int partitionHole(int[] arr, int start, int end) {
        int key = arr[start];
        while (start<end) {
            while (start<end && key<=arr[end]) {
                end--;
            }
            arr[start] = arr[end];
            while (start<end && key>=arr[start]){
                start++;
            }
            arr[end] = arr[start];
        }
        arr[start] = key;
        return start;
    }
 
    private static void swap(int[] arr, int start, int end) {
        int tmp = arr[start];
        arr[start] = arr[end];
        arr[end] = tmp;
    }
}

 我们还有三数取中法, 前后指针法,不递归进行快排,我直接附代码啦~~!!

public static void insertSort2(int[] array,int start, int end){
        for (int i = start; i <= end; i++) {
            int indix = array[i];
            int j = i-1;
            for ( ; j >= start ; j--) {
                if(array[j] > indix){
                    array[j+1] = array[j];
                }else {
                    break;
                }
            }
            array[j+1] = indix;
        }
    }
    private static void quick(int[] arr,int left,int right){
        if(left >= right){
            return;
        }
        if(right-left+1 <= 7){
            insertSort2(arr,left,right);
            return;
        }
        int ret = midNumber(arr,left,right);
        swap(arr,left,ret);
        int pivot = partitionHole(arr,left,right);
        quick(arr,left,pivot-1);
        quick(arr,pivot+1,right);
 
    }
    private static int midNumber(int[] array, int left, int right){
        int mid = (left+right)/2;
        if(left > right){
            if(mid > left){
                return left;
            }else if(mid < right){
                return right;
            }else {
                return mid;
            }
        }else {
            if(mid > right){
                return right;
            }else if(mid < left){
                return left;
            }else {
                return mid;
            }
        }
    }
    public static void quickSort(int[] arr){
        quick(arr,0,arr.length-1);
    }

//指针法
    private static int partition(int[] arr,int start,int end){
        int k = arr[start];
        int pre = start;
        int cur = start+1;
        while(cur < end){
            while (arr[cur]<k && arr[++pre] != arr[cur]){
                swap(arr,pre,cur);
            }
            cur++;
        }
        swap(arr,pre,start);
        return pre;
    }

//非递归的快速排序
    private static int partitionHole1(int[] arr,int start,int end){
        int tmp = arr[start];
        while (start<end){
            while (start<end && arr[end] >= tmp){
                end--;
            }
            arr[start] = arr[end];
            while (start<end && arr[start] <= tmp){
                start++;
            }
            arr[end] = arr[start];
        }
        arr[start] = tmp;
        return start;
    }
    private static void quick1(int[] arr,int left,int right){
        Stack<Integer> stack = new Stack<>();
        int pivot = partitionHole1(arr,left,right);
 
        if(pivot > left+1) {
            stack.push(left);
            stack.push(pivot - 1);
        }
        if(pivot < right-1) {
            stack.push(pivot + 1);
            stack.push(right);
        }
 
        while(!stack.empty()){
            right = stack.pop();
            left = stack.pop();
            pivot = partitionHole1(arr,left,right);
            if(pivot > left+1) {
                stack.push(left);
                stack.push(pivot - 1);
            }
            if(pivot < right-1) {
                stack.push(pivot + 1);
                stack.push(right);
            }
        }
    }
    public static void quickSort1(int[] arr){
        quick1(arr,0,arr.length-1);
    }