计算机网络：差错控制

比特在传输过程中可能会产生差错，1可能会变成0，0也可能会变成1，这就是比特差错。比特差错是传输差错中的一种。

通常利用编码技术进行差错控制,主要有两类:自动重传请求ARQ和前向纠错FEC。

• 在 ARQ方式中，接收端检测到差错时，就设法通知发送端重发，直到接收到正确的码字为止。
• 在FEC方式中，接收端不但能发现差错，而且能确定比特串的错误位置，从而加以纠正。

因此，差错控制又可分为检错编码和纠错编码。

检错编码

检错编码都采用冗余编码技术，其核心思想是在有效数据（信息位）被发送前，先按某种关系附加一定的冗余位，构成一个符合某一规则的码字后再发送。当要发送的有效数据变化时，相应的冗余位也随之变化，使得码字遵从不变的规则。接收端根据收到的码字是否仍符合原规则来判断是否出错。

常见的检错编码有奇偶校验码和循环冗余码。

1.奇偶校验码

奇偶校验码是奇校验码和偶校验码的统称，是一种最基本的检错码。它由n-1位信息元和1位校验元组成，如果是奇校验码，那么在附加一个校验元后，码长为n的码字中“1”的个数为奇数,这是奇数校验码 ;如果是偶校验码，那么在附加一个校验元以后，码长为n的码字中“1”的个数为偶数。它只能检测奇数位的出错情况，(如果有一组刚好出错，1的奇偶却不变，则无法查清楚是否出错)。

2.循环冗余码

循环冗余码 (Cyclic Redundancy Code, CRC) 又 称多项式码。一个 k 位帧可以视为从 $X^{k-1}$ 到 $ X^{0}$ 的 k 次多项式的系数序列, 这个多项式的阶数为 k-1, 例如, 1110011 有 7 位, 表示成多项式是 $X^6+X^5+X^4+X+1$

给定一个m bit的帧或报文, 发送器生成一个r bit的序列，称为帧检验序列(FCS) 就是余数。这样所形成的帧将由m+r比特组成。发送方和接收方事先商定一个多项式G(x)(最高位和最低位必须为1)，使这个带检验码的帧刚好能被预先确定的多项式G(x)整除。接收方用相同的多项式去除收到的帧，如果无余数，那么认为无差错。
假设一个帧有m位，其对应的多项式为Mx)，则计算冗余码的步骤如下:

1. 加0。假设G(x)的阶为r(阶数是指最高位的次数，不是总式子的长度)，在帧的低位端加上r个0。
2. 模2除。利用模2除法（就是异或），用G(x)对应的数据串去除1）中的数据串，得到的余数即为冗余码（共r位，前面的0不可省略)。

注意:循环冗余码(CRC)是具有纠错功能的，只是数据链路层仅使用了它的检错功能，检测到帧出错则直接丢弃。

纠错编码

最常见的纠错编码是海明码，其实现原理是在有效信息位中加入几个校验位形成海明码，并把海明码的每个二进制位分配到几个奇偶校验组中。当某一位出错后，就会引起有关的几个校验位的值发生变化，这不但可以发现错位，而且能指出错位的位置，为自动纠错提供依据。

现以数据码 1010 为例讲述海明码的编码原理和过程。

(1) 确定海明码的位数

设 n 为有效信息的位数, k 为校验位的位数, 则信息位 n 和校验位 k 应满足 $n+k\le 2^k-1$ (若要检测两位错, 则需再增加 1 位校验位, 即 k+1 位)
海明码位数为 $n+k=7\le 2^3-1$ 成立, 则 n 、 k 有效。设信息位为 $D_4{D}_3{D}_2{D}_1(1010)$ , 共 4 位, 校验位为 $P_3{P}_2{P}_1$ , 共 3 位, 对应的海明码为$H_7{H}_6{H}_5{H}_4{H}_3{H}_2{H}_1$。

(2)确定校验位的分布

规定校验位 $P_i$ 在海明位号为 $2^{i-1}$ 的位置上, 其余各位为信息位, 因此有:
$P_1$ 的海明位号为 $2^{i-1}=2^0=1$ , 即 $H_1$ 为 $P_1$ 。
$ P_{2}$ 的海明位号为 $ 2^{i-1}=2{1}=2$ , 即 $H_2$ 为 $P_2$ 。
$ P_{3}$ 的海明位号为 $2^{i-1}=2^2=4$ , 即 $H_4$ 为 $P_3$ 。
将信息位按原来的顺序揷入, 则海明码各位的分布如下:

$\begin{array}{lllllll}{H}_7& H_6& H_5& H_4& H_3& H_2& H_1\\ D_4& D_3& D_2& P_3& D_1& P_2& P_1\end{array}$

(3) 分组以形成校验关系

每个数据位用多个校验位进行校验, 但要满足条件: 被校验数据位的海明位号等于校验该数 据位的各校验位海明位号之和。另外, 校验位不需要再被校验。分组形成的校验关系如下。

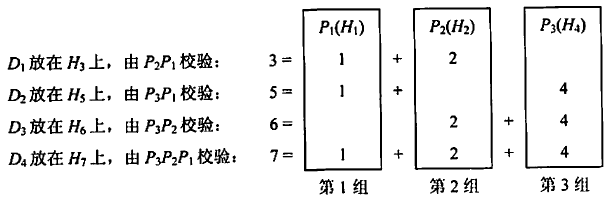
(4) 校验位取值

校验位 $P_i$ 的值为第 i 组 (由该校验位校验的数据位) 所有位求异或。 根据（3）中的分组有

$P_1=D_1\oplus D_2\oplus D_4=0\oplus 1\oplus 1=0$
$P_2=D_1\oplus D_3\oplus D_4=0\oplus 0\oplus 1=1$
$P_3=D_2\oplus D_3\oplus D_4=1\oplus 0\oplus 1=0$

所以, 1010 对应的海明码为 1010010(下画线为校验位, 其他为信息位)。

(5)海明码的校验原理

每个校验组分别利用校验位和参与形成该校验位的信息位进行奇偶校验检查, 构成 k 个校验方程:

$\begin{array}{l}{S}_1=P_1\oplus D_1\oplus D_2\oplus D_4\\ S_2=P_2\oplus D_1\oplus D_3\oplus D_4\\ S_3=P_3\oplus D_2\oplus D_3\oplus D_4\end{array}$

若 $S_3{S}_2{S}_1$ 的值为 “ 000 ”, 则说明无错; 否则说明出错, 且这个数就是错误位的位号, 如 $S_3{S}_2{S}_1=001$ , 说明第 1 位出错, 即 $H_1$ 出错, 直接将该位取反就达到了纠错的目的。