【JAVA】二分查找

用二分查找来查找数组里出现的元素是一个高效率的查找，但它的局限性是  数组的元素必须有序

二分查找的原理就是：循环找数组的中间元素，如果要找的key比数组的中间元素小，就说明这个key可能在中间值的左半部分（数组有序），如果要查找的key值比数组中间大，说明这个key值可能在中间元素的右半部分

所以二分查找也叫做折半查找，简单来说就是一半一半的来找，减少查询的次数，提高查询的效率

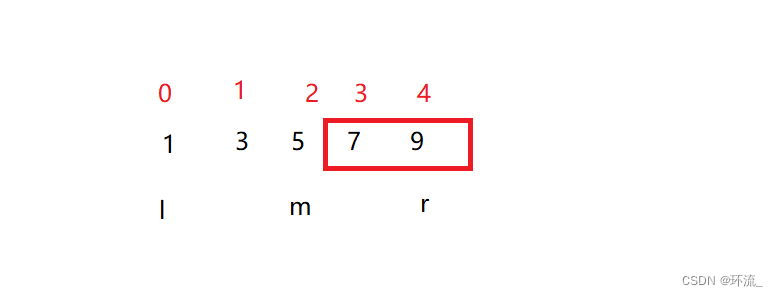
比如说我们有一个有序数组：1  3   5    7   9

我们定义一个left（l）为数组的第一个元素下标，定义一个right（r）为数组的最后一个元素下标，

再定义一个mid（m）为数组中间元素的下标

 比如说我们现在想在这个数组里面找到元素key为9的下标

我们拿9和mid5进行比较大小，9>5 ， 所以9这个元素一定在m的右半部分

 接着m的左半部分就不管了，把left重新定义为mid+1，然后mid为left+right的中间位置

此时m=7 < 9; 还是小于key值，说明要查询的key值可能还在m的左半部分，根据刚才的过程再循环一次，再次把 left = mid + 1，此时left和right相遇，m值等于left加right的中间值

 

 然后在拿mid下标的值和key比较，发现array[mid] == key；所以此时返回mid下标即可

---

上述过程表示要找的key值在数组中存在的例子

已经讲了key > array[mid] 的过程，这属于要查找的元素出现在m的右半部分，同样的，如果要找的是小于array【mid】的值同样的过程，找m的左半部分即可

下面来说说要找的key在数组中不存在的情况，这也是给我们的循环提供了循环条件~

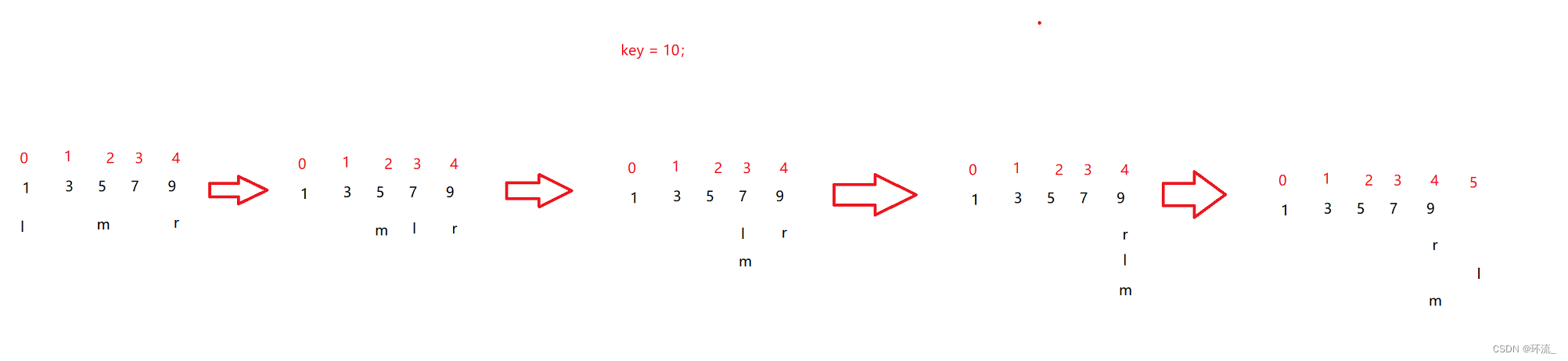
假如我们现在要找key为8在数组中的下标，所以看看停止折半的循环条件是啥

根据上图的箭头，前面三个箭头是我们之前讲的查找9的过程，现在我们查找8

来到第三个箭头，此时left == right ，然后m = （left + right）/2 

接着我们要找key=8，8 < array[mid]，说明10可能出现在m的右半部分，那么此时 right = mid-1；

然后我们发现此时left > right 了，说明我们已经把该找的数字都找了，每发现8的存在

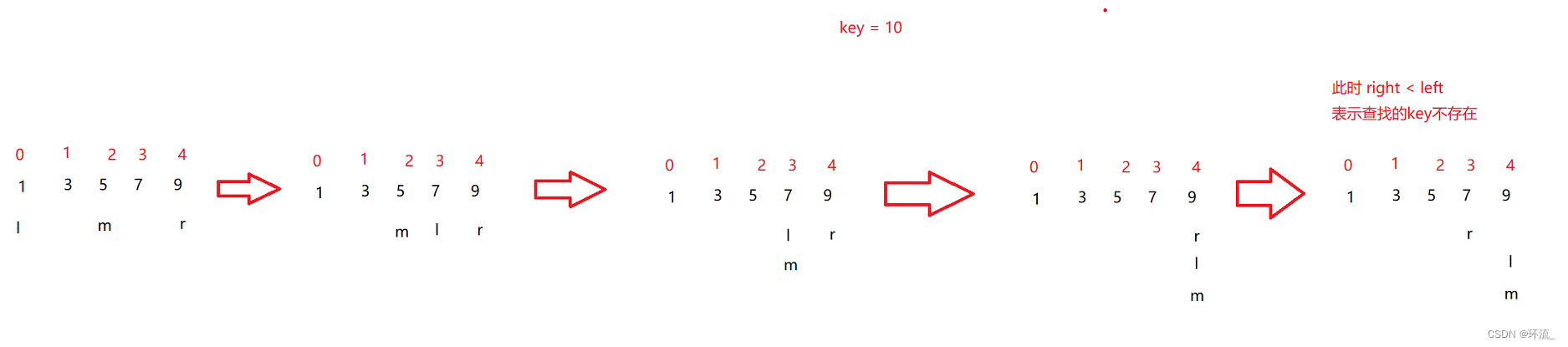
再比如我们想找的是10；

根据上图，我们发现当查找10，说明在第三个箭头的m的右半部分，然后left = mid + 1；

不幸的是，此时的 left 又有又大于 right了，说明要查找的10不存在

所以，综上所述，折半的循环条件就是  left <= right

下面是代码展示~

二分查找函数，找到返回下标，找不到返回  -1

public class 二分查找 {
    public static void main(String[] args) {
        int[] arr = {1,4,7,8,9,10,14,16,19};
        System.out.println(binarySearch(arr,90));
    }
    public static int binarySearch(int[] array,int key){
        int left = 0;
        int right = array.length-1;
        while (left <= right){
            int mid = (left + right) / 2;
            if(array[mid] < key){
                left = mid + 1;
            } else if (array[mid] == key) {
                return mid;
            }else {
                right = mid - 1;
            }
        }
        return -1;
    }
}