【python】Numpy统计函数总结

函数列表

注

• 标有星号*的表示存在一个nan开头的同名函数，可以忽略非有效值。例如median对应nanmedian。

上表中大部分函数可以顾名思义，下面对相关系数和直方图做进一步的介绍

相关系数

首先回忆一下协方差的概念，对于$X,Y$两组样本，其协方差可以表示为

$$cov(X,Y)=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{n-1}$$

numpy中的协方差函数cov，得到的是一个矩阵，分别用于描述$X-X,X-Y,Y-X,Y-Y$这四对协方差，对于数组与其自身的协方差，其协方差表达式退化为

$$cov(X,X)=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(x_i-\bar{x})}{n-1}=\frac{{\sum }_{i=1}^n(x_i-\bar{x}{)}^2}{n-1}$$

这和标准差的公式是极为相近的，Numpy中的标准差公式是

$$std(X)==\sqrt{\frac{{\sum }_{i=1}^n(x_i-\bar{x}{)}^2}{n}}$$

下面输入代码验证一下

>>> x = np.arange(10)
>>> np.cov(x,x[::-1])
array([[ 9.16666667, -9.16666667],
       [-9.16666667,  9.16666667]])
>>> np.std(x)**2*10/9
9.166666666666666
1
2
3
4
5
6

其中[::-1]表示将数组前后倒置。

在理解协方差与方差之后，就可以理解相关系数，记$C_{ij}$为第$i$和第$j$列数组之间的协方差，那么相关系数可表示为

$$R_{ij}=\frac{C_{ij}}{\sqrt{C_{ii}{C}_{j}j}}$$

可见，当$i==j$时，数组与其自身的相关系数为1。

>>> np.corrcoef(x,x[::-1])
array([[ 1., -1.],
       [-1.,  1.]])
1
2
3

直方图

histogram用于得到数据直方图数据，histogram2d表示二维的直方图，histogramdd表示高维直方图。其输入参数可表示为

histogram(a, bins=10, range=None, normed=None, weights=None, density=None)
1

其中

• a是待统计数组；
• bins指定区间数
• range 表示统计区域，例如[0,1]表示统计从0到1的值
• weights 表示数组权重
• density 为True时，返回概率密度；为False时，返回元素个数

a = np.random.normal(size=1000)
y, x = np.histogram(a, bins=20)
print(y)
>>> print(y)
#[  1   1   1   1   6  11  29  53  74 101 128 140 131 112  90  59  29  18  12   3]
1
2
3
4
5

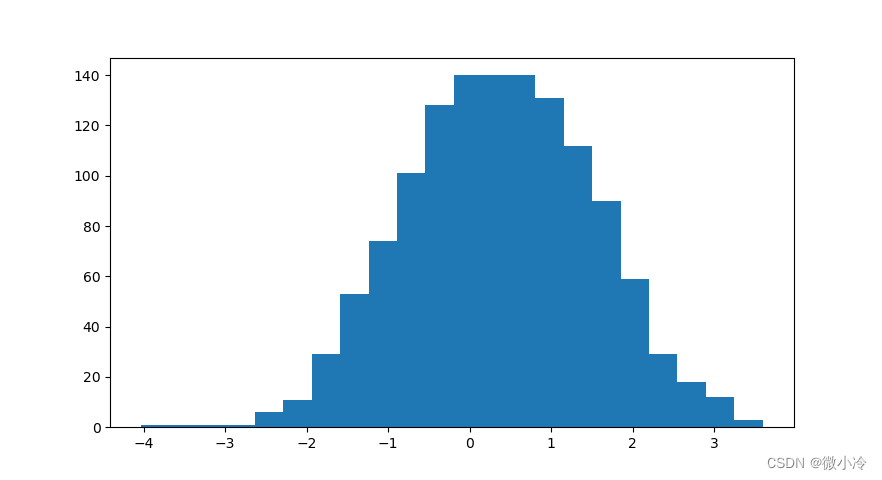
得到x长度为10，表示每个区间中的元素个数；y的长度为11，表示区间的起止值。

这个结果可以画图看一下

import matplotlib.pyplot as plt
plt.bar(x[:-1], y, width=1, align='edge')
1
2

histogram_bin_edges和histogram功能相同，但只输出直方图的边缘，即上面的y。

digsize(a,y)用于统计数组a中的值对应在y中对应区间的位置，例如y=[1,2,3]，则1.5在1和2之间，属于第一个区间；0在1前面，是第0个区间。对应histogram的例子，表示找到a在y中的位置。

bincount可以用于统计正整数的个数

>>> test = [np.random.randint(20) for _ in range(500)]
>>> np.bincount(test)
array([29, 23, 19, 21, 29, 16, 16, 33, 23, 32, 20, 28, 29, 22, 19, 32, 27,
       33, 19, 30], dtype=int64)
1
2
3
4