代码随想录45——动态规划：70爬楼梯（进阶版）、322零钱兑换、279完全平方数

1.70爬楼梯（进阶版）

参考：代码随想录，70爬楼梯（进阶版）；力扣题目链接

1.1.题目

1.2.解答

使用完全背包的思想来解决爬楼梯问题的关键是如果可以一步一个台阶、一步两个台阶…一直到一步m个台阶，问有多少种方法可以爬到楼梯顶，这样和完全背包的问题就更加契合了。

这道题目 我们在动态规划：爬楼梯 中已经讲过一次了，原题其实是一道简单动规的题目。既然这么简单为什么还要讲呢，其实本题稍加改动就是一道面试好题。

改为：一步一个台阶，两个台阶，三个台阶，…，直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢？

1阶，2阶，… m阶就是物品，楼顶就是背包。

每一阶可以重复使用，例如跳了1阶，还可以继续跳1阶。

问跳到楼顶有几种方法其实就是问装满背包有几种方法。

此时大家应该发现这就是一个完全背包问题了！

和昨天的题目动态规划：377. 组合总和 Ⅳ 基本就是一道题了。

动规五部曲分析如下：

1.确定dp数组以及下标的含义

dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法。

2.确定递推公式

在动态规划：494.目标和、 动态规划：518.零钱兑换II 、动态规划：377. 组合总和 Ⅳ中我们都讲过了，求装满背包有几种方法，递推公式一般都是 dp[i] += dp[i - nums[j]];

本题呢，dp[i]有几种来源，dp[i - 1]，dp[i - 2]，dp[i - 3] 等等，即：dp[i - j]

那么递推公式为：dp[i] += dp[i - j]

3.dp数组如何初始化

既然递归公式是 dp[i] += dp[i - j]，那么dp[0] 一定为1，dp[0]是递归中一切数值的基础所在，如果dp[0]是0的话，其他数值都是0了。

下标非0的dp[i]初始化为0，因为dp[i]是靠dp[i-j]累计上来的，dp[i]本身为0这样才不会影响结果

4.确定遍历顺序

这是背包里求排列问题，即：1、2 步 和 2、1 步都是上三个台阶，但是这两种方法不一样！

所以需将背包容量放在外循环，物品放在内循环。

每一步可以走多次，这是完全背包，内循环需要从前向后遍历。

5.举例来推导dp数组

介于本题和动态规划：377. 组合总和 Ⅳ几乎是一样的，这里我就不再重复举例了。

以上分析完毕，C++代码如下：

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) { // 遍历背包
            for (int j = 1; j <= m; j++) { // 遍历物品
                if (i - j >= 0) dp[i] += dp[i - j];
            }
        }
        return dp[n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

代码中m表示最多可以爬m个台阶，代码中把m改成2就是本题70.爬楼梯可以AC的代码了

2.322零钱兑换

参考：代码随想录，322零钱兑换；力扣题目链接

2.1.题目

2.2.解答

题目中说每种硬币的数量是无限的，可以看出是典型的完全背包问题。

动规五部曲分析如下：

1.确定dp数组以及下标的含义

dp[j]：凑足总额为j所需钱币的最少个数为dp[j]

2.确定递推公式

凑成总额为j，所需要的钱币个数有两个来源：

• 不使用当前遍历到的面值为coins[i]的钱币，那么就是使用之前0到coins[i-1]的所有前面凑成总额j，所以钱币个数就是dp[i-1][j]，换成一维的dp数组就是dp[j]。注意：这个dp[j]实际上是二维dp数组中上一行的dp[j]。
• 使用当前遍历到的面值为coins[i]的钱币，那么就是使用之前0到coins[i]的所有前面凑成总额j-coins[i]，所以钱币个数就是dp[i][j-coins[i]] + 1，换成一维的dp数组就是dp[j-coins[i]]。注意：这个dp[j-coins[i]]是当前行的dp数组。

因为是要求最小的硬币个数，所以递推公式为：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

3.dp数组如何初始化

首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;

其他下标对应的数值呢？

考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。

所以下标非0的元素都是应该是最大值。

代码如下：

vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
1
2

疑问：这里并不是特别理解，感觉使用二维的dp数组也无法解释的通。如果使用二维dp数组的化，背包容量>0的那些倒是可以解释的通，因为金币是0，只有使用无穷多的金币，才可能凑成总额>0。

但是总额是0呢？为什么不可以是1个面值为0的金币？或许可以解释为这里要求最小值？所以总额是0的话，面值为0的金币也不用放，结果总额直接就是0了？

4.确定遍历顺序

本题求钱币最少个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。

注意：这里是求集合中钱币的个数，所以1, 2, 1和1, 1, 2是一样的，最少个数都是3，因此不管是排列还是组合只影响里面具体的排列顺序，集合中元素的个数还是一样的。所以本题并不强调集合是组合还是排列。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

在动态规划专题我们讲过了求组合数是动态规划：518.零钱兑换II，排列数是动态规划：377. 组合总和 Ⅳ。

所以本题的两个for循环的关系是：外层for循环遍历物品，内层for遍历背包 或者 外层for遍历背包，内层for循环遍历物品都是可以的！

那么我采用coins放在外循环，target在内循环的方式。

本题钱币数量可以无限使用，那么是完全背包。所以遍历的内循环是正序

综上所述，遍历顺序为：coins（物品）放在外循环，target（背包）在内循环。且内循环正序。

5.举例推导dp数组

以输入：coins = [1, 2, 5], amount = 5为例

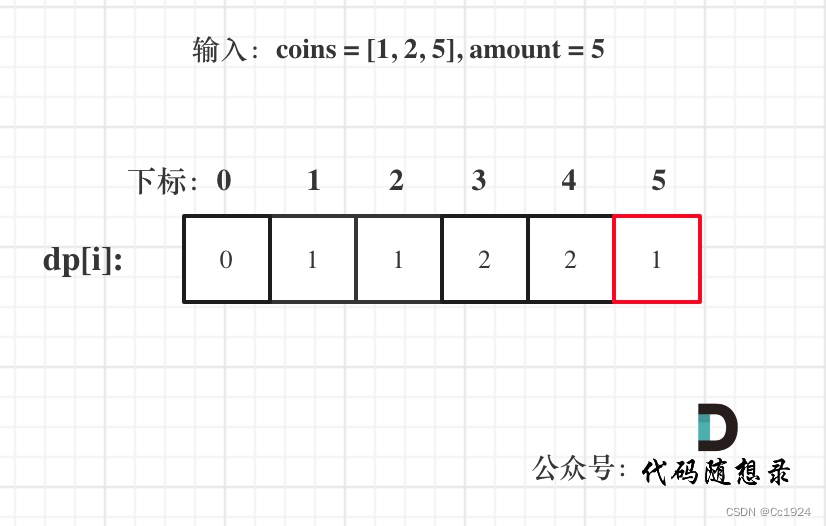
TODO：给出代码如下，两种for循环的顺序都可以，没有先后的要求。

// 使用组合问题的for循环：先遍历物品，再遍历背包
int coinChange(vector<int>& coins, int amount) 
{
    vector<int> dp(amount + 1, INT_MAX);
    dp[0] = 0;
    for (int i = 0; i < coins.size(); i++)    // 遍历物品
    {
        for (int j = coins[i]; j <= amount; j++)    // 遍历背包
        {
            // 如果dp[j - coins[i]]是初始值则跳过
            if (dp[j - coins[i]] != INT_MAX) 
            {
                dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
            }
        }
    }
    if (dp[amount] == INT_MAX) 
   		return -1;
    return dp[amount];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

3.279完全平方数

参考：代码随想录，279完全平方数；力扣题目链接

3.1.题目

3.2.解答

可能刚看这种题感觉没啥思路，又平方和的，又最小数的。

我来把题目翻译一下：完全平方数就是物品（可以无限件使用），凑个正整数n就是背包，问凑满这个背包最少有多少物品？

感受出来了没，这么浓厚的完全背包氛围，而且和昨天的题目动态规划：322. 零钱兑换就是一样一样的！

动规五部曲分析如下：

1.确定dp数组（dp table）以及下标的含义

dp[j]：和为j的完全平方数的最少数量为dp[j]

2.确定递推公式

dp[j] 可以由dp[j - i * i]推出， dp[j - i * i] + 1 便可以凑成dp[j]。

此时我们要选择最小的dp[j]，所以递推公式：dp[j] = min(dp[j - i * i] + 1, dp[j]);

3.dp数组如何初始化

dp[0]表示 和为0的完全平方数的最小数量，那么dp[0]一定是0。

有同学问题，那0 * 0 也算是一种啊，为啥dp[0] 就是 0呢？

看题目描述，找到若干个完全平方数（比如 1, 4, 9, 16, …），题目描述中可没说要从0开始，dp[0]=0完全是为了递推公式。

非0下标的dp[j]应该是多少呢？

从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的，所以非0下标的dp[j]一定要初始为最大值，这样dp[j]在递推的时候才不会被初始值覆盖。

4.确定遍历顺序

我们知道这是完全背包，

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

在动态规划：322. 零钱兑换中我们就深入探讨了这个问题，本题也是一样的，是求最小数！

所以本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的！

我这里先给出外层遍历背包，内层遍历物品的代码：

vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i <= n; i++) { // 遍历背包
    for (int j = 1; j * j <= i; j++) { // 遍历物品
        dp[i] = min(dp[i - j * j] + 1, dp[i]);
    }
}
1
2
3
4
5
6
7

5.举例推导dp数组

已输入n为5例，dp状态图如下：

TODO：也是最后给出代码，两种for循环的顺序都可以

// 组合问题：先遍历物品，再遍历背包
int numSquares(int n) 
{
    vector<int> dp(n+1, INT32_MAX);
    dp[0] = 0;
    for(int i = 0; i*i <= n; i++)
    {
        for(int j = i*i; j <= n; j++)
        {
            if(dp[j-i*i] != INT32_MAX)
            {
                dp[j] = min(dp[j], dp[j-i*i] + 1);
            }
        }
    }
    return dp[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17