纯手撸一个神经网络（只用numpy识别mnist数据集，全代码）

全代码

纯手撸一个识别mnist手写数据集的2层DNN网络，所有库函数的低层NumPy代码都已给出，这串代码直接运行就能跑！不需要其他文件。
如果没装TensorFlow和matplotlib的童鞋可以在终端输入 pip install tensorflow 和 pip install matplotlib 进行安装。

import numpy as np
import matplotlib.pylab as plt
import tensorflow as tf #引入tensorflow只是为了导入mnist数据集

#下面一大段都是定义函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def sigmoid_grad(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)


def relu(x):
    return np.maximum(0, x)


def relu_grad(x):
    #grad = np.zeros(x)
    #grad[x>=0] = 1
    x = np.where(x>=0,1,0)
    return x


def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x)  # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))


def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t) ** 2)


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size


def softmax_loss(X, t):
    y = softmax(X)
    return cross_entropy_error(y, t)


def numerical_gradient(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)

    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2 * h)

        x[idx] = tmp_val  # 还原值
        it.iternext()

    return grad



class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.dot(x, W1) + b1
        #z1 = sigmoid(a1)
        z1 = relu(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y

    # x:输入数据, t:监督数据
    def loss(self, x, t):
        y = self.predict(x)

        return cross_entropy_error(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W: self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

    def gradient(self, x, t):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']
        grads = {}

        batch_num = x.shape[0]

        # forward
        a1 = np.dot(x, W1) + b1
        #z1 = sigmoid(a1)
        z1 = relu(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        # backward
        dy = (y - t) / batch_num
        grads['W2'] = np.dot(z1.T, dy)
        grads['b2'] = np.sum(dy, axis=0)

        da1 = np.dot(dy, W2.T)
        #dz1 = sigmoid_grad(a1) * da1
        dz1 = relu_grad(a1) * da1
        grads['W1'] = np.dot(x.T, dz1)
        grads['b1'] = np.sum(dz1, axis=0)

        return grads


def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1

    return T

#开搞
# 读入数据
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0 #归一化
x_train = x_train.reshape(-1,784)  # flatten, (60000,28,28)变（60000,784）
x_test = x_test.reshape(-1,784)  # flatten, (10000,28,28)变（10000,784）
y_train = _change_one_hot_label(y_train) #标签变独热码，才能和前向传播softmax之后的结果维度匹配，才能相减算误差
y_test = _change_one_hot_label(y_test) #标签变独热码

#两层DNN(隐藏层50个神经元，784*50*10)，激活函数是relu，可自己改成sigmoid，损失函数是交叉熵误差，输出层是softmax，优化函数是SGD
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

#超参数设置
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 512
learning_rate = 0.05

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

#训练
for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    y_batch = y_train[batch_mask]

    # 梯度
    # grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, y_batch)

    # 更新
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    loss = network.loss(x_batch, y_batch)
    train_loss_list.append(loss)

    #每一个epoch打印训练和测试的准确率
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, y_train)
        test_acc = network.accuracy(x_test, y_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)

# 绘制 loss 曲线
plt.subplot(1,2,1)
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Step')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_list, label="$Loss$")  # 逐点画出loss值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标

# 绘制 Accuracy 曲线
plt.subplot(1,2,2)
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(train_acc_list, label="$train_{acc}$")  # 逐点画出train_acc值并连线
plt.plot(test_acc_list, label="$test_{acc}$")  # 逐点画出test_acc值并连线
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229

 

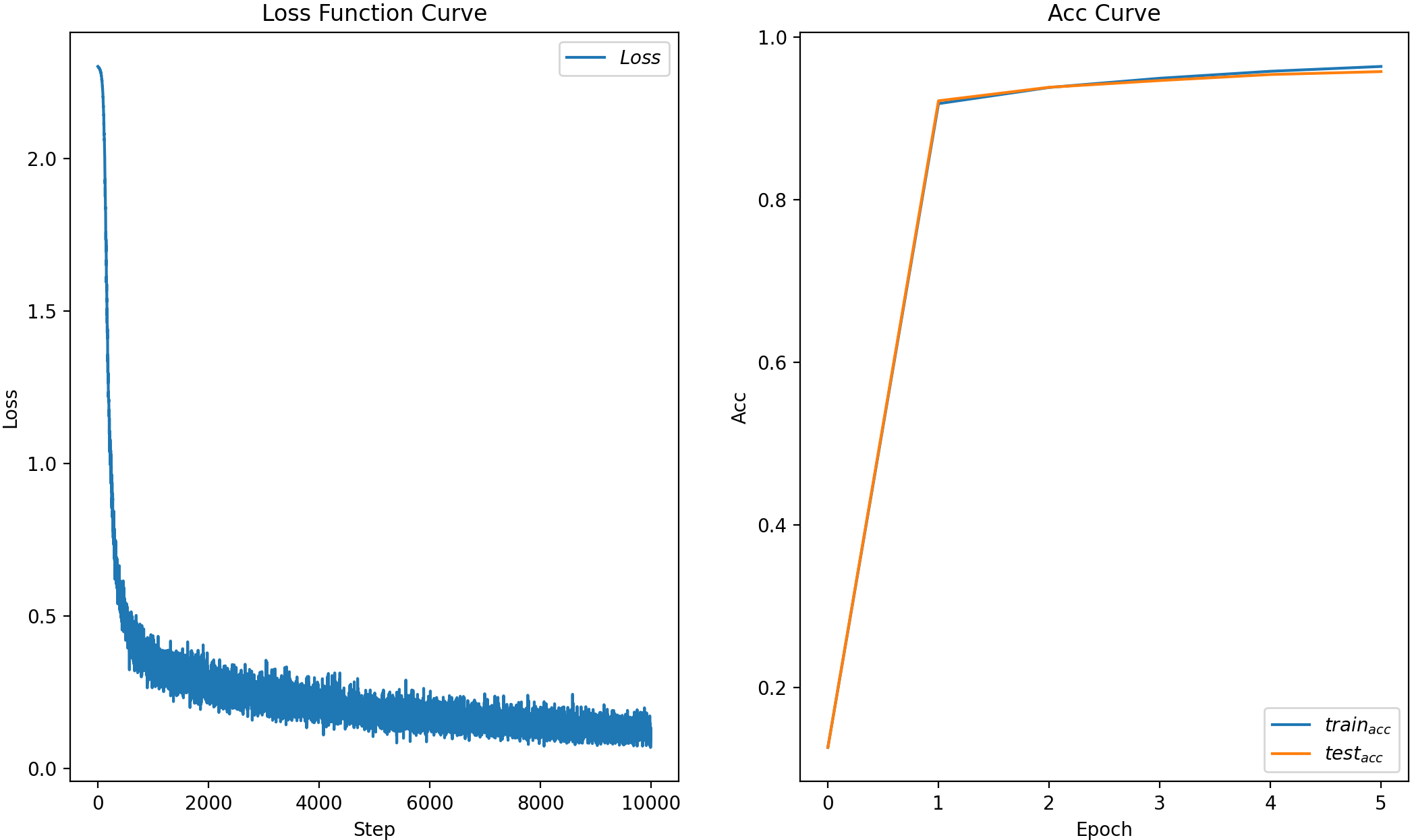
总结

简单的两层网络（W个数：784*50+50*10，b个数：50+10），就能实现95%的准确率，且没有过拟合。
batch_size调大一点loss就不会这么震荡，训练周期长一点acc会更大，学习率越大训练越快，但太大会跑飞，都可以调来玩玩。
上面的激活函数是选了relu，可自己改成sigmoid，代码里relu换成sigmoid就行，事实证明是relu好一点。
上面的优化器是SGD（随机梯度下降），还有Momentum、AdaGrad、Adam等等，一般用Adam会有更好效果。
所以可以总结神经网络学习全貌：

前提

神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的

过程称为“学习”。神经网络的学习分成下面4个步骤。

步骤1（mini-batch）

从训练数据中随机选出一部分数据，这部分数据称为mini-batch。我们

的目标是减小mini-batch的损失函数的值。

步骤2（计算梯度）

为了减小mini-batch的损失函数的值，需要求出各个权重参数的梯度。

梯度表示损失函数的值减小最多的方向。

步骤3（更新参数）

将权重参数沿梯度方向进行微小更新。

步骤4（算误差、精度）

每次循环都算一下误差，若到一次epoch，算一下精度。

步骤5（重复）

重复步骤1、步骤2、步骤3、步骤4。

 
更多深度学习入门内容可以看看这篇哦《一文极速理解深度学习》。