数电学习（十、脉冲波形的产生和整形）（一）

---

引言

• 纯数字的内容基本已经结束

• 但是还有一件事没有解决，在数字电路当中，我们认为方波到处都存在，但是实际上波形发生是要我们自己做的

• 把第三章（门电路）和电路原理（等效，过渡过程）结合在一起

• 在数字信号中，门电路是处理信号的，信号是用离散的电压序列来表达，所以，每一个门电路的输出其实都是一个电压源；每一个门电路的输入，如果是CMOS型的，输入不取电流，电压信号传递，输入等效一个小电容；如果是TTL的，输入是有一个管，输入是低电平上面来一个大电流，输入时高电平，趴着的PN管，PN结反向。

• 任务：产生理想的波形

• ！！！！注意：这章讲的触发器是真触发（trigger），不是前面说的存储那些（flip flop翻转）

概述

• 对于脉冲波形，我们关注它的发生和整形

1. 获取脉冲的方法
   （1）脉冲波形发生电路
   （2）脉冲波形整形电路

• 对于一个脉冲波形，主要关注三条：周期，占空比，斜率

2. 描述矩阵脉冲特性主要参数
   

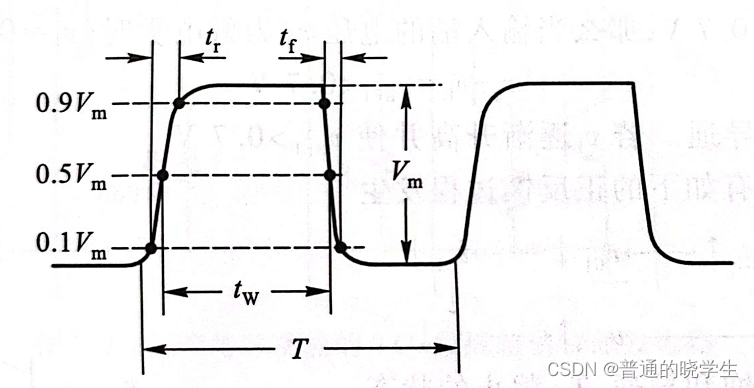
施密特触发器（常用的一类脉冲整形电路）

用门电路组成的施密特触发器

Voh=Vdd，Vol=0，Vth=1/2Vdd，且R1

• 想知道输入输出之间的关系（电压转移特性曲线）
• 0-1的过程分析如下：
  （1） Vi = 0时，Vo = 0（如果说的是逻辑0，Vo也是逻辑0，但是如果看具体的电压值，如果有差，就会形成电流，Va就是一个分压，但是一定是在逻辑0，不会超过逻辑0）
  

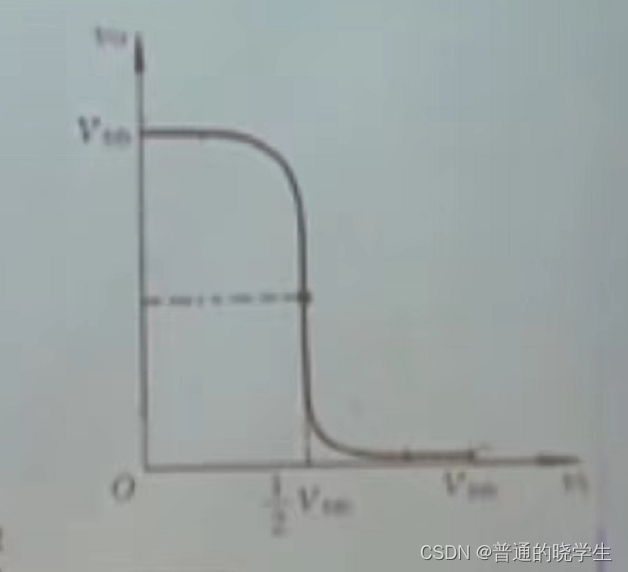
（2）当Vi增大时，Va也上升，上升的值是（Vi-Vo）在Va的分压，当Va上升至1/2Vdd时（也就是上面每一个反相器的电压传输特性曲线的横轴中点），Va再上升，Vo1就下降，Vo就上升，导致Va也上升。这是一个正反馈，这个正反馈会把Vo推高，最后变到理想的高电平

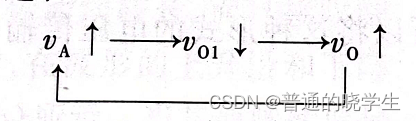
（3）Va的变化一开始是因为Vi的变化，而Vi在变化时，Vo还没有改变，所以时（Vi-Vo）的分压，这个值倒算回来，也就是Vi在变化当中让Va变成Vth，所以可以倒推出来Vi的值

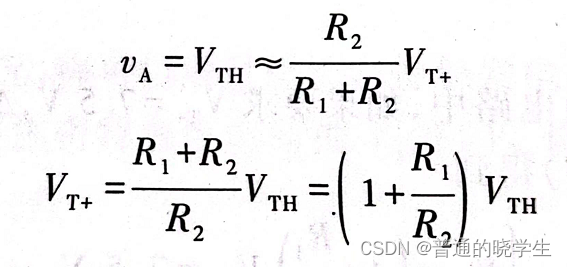
• 1-0的过程分析如下：
  （1）当Vi = 1时，Vo = 1
  （2）当Vi下降至Va = Vth时，进入传输特性曲线的放大区，使电路迅速跳变至Vo=Vol
  
  (3)在整个变化过程Va就是Vdd-Vi，后面加Vi是因为算出来分压还要加上基准的Vi
  

• 得到传输特性曲线
  

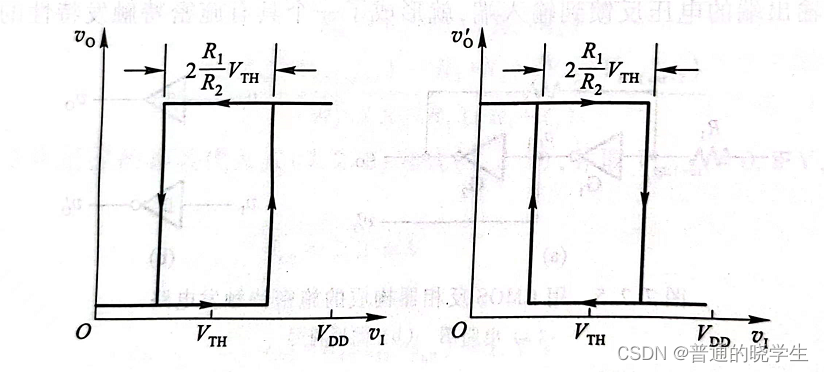
• 问题：为什么R2要大于R1？

• 如果R1>R2，如果Vi是低电平，Vo也是低电平，这没有问题，但是当Vi上升时，即便Vi已经上升到最理想的电压Vdd，Va也不可能到达门电路的门槛电压（1/2Vdd），也就是不可能发生翻转，也就不存在上面推导的公式。

• 换句话说，R2如果小的话，电路就被锁死了，锁死了就相当于前面讲的锁存器

• 特点：
  （1）V+和V-两个门槛电压值不一样
  （2）两个变化过程都是正反馈，也就是说边沿会特别抖

• 如果一个器件有这样的标识，那么证明它的Vi和Vo之间有前面所论述的滞环特性
• 但是从逻辑关系来讲，这个符号应该是一个正向的缓冲，Vo和Vi的逻辑关系不变。也就是说如果换成第三章的其他运算，它只表示V+和V-不一样，而且边沿特性特别好，但是并不影响电路的逻辑功能

集成施密特触发器

TTL工艺

电路结构和工作原理

• 不是搭接而成，而是通过之前讲过的TTL工艺或者CMOS工艺制造的集成的施密特触发器

• 我们拿到的集成施密特触发器都是成熟的设计，目标都是为了能满足能够达到那个滞环特性，所以我们围绕这个去分析（R1=2k欧，R2=1.4k欧，Re=480欧）
  

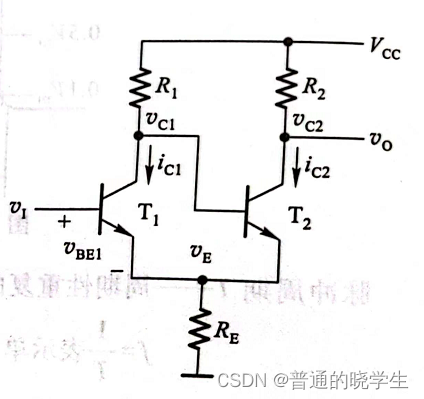
• Ve的电压值其实会和T1和T2的导通关系相关

• 在数字电路中，如果我们好奇输入输出关系，可以做这样的假设。当输入是逻辑低电平，即Vi=0时，那么T1截止，如果参数合理，T2可以饱和导通，这时Ve的电压就是R2和Re的一个分压

• 当输入时逻辑高电平的时候，T1饱和导通，Vc1就等于Ve加上T1的饱和导通电压值，这样一来T2就截止了，所以Ve就变成了Re和R1之间的分压

• 也就是说，当输入为高低电平的时候，Ve的值不同。所以需要关心两件事：
  （1）如果输入是高电平，当我的高电平往低电平变化的过程中，最后的目标一定是变到输入为0，但是中间的过程我会关心，输入变到多少能使电路状态发生变化
  （2）如果输入是低电平，当我的低电平往高电平变化的过程中，哪个值会让它发生变化

• 问题：当输入从0升高时，什么时候电路的输出会发生变化？

• 输入增高一开始不会发生变化，一直增长到Ve+0.7的时候，输出就会发生变化，下面这一串就会产生。
  

• （因为电阻参数不同，ic2下降的会比ic1上升的快，所以Ve下降）

• 正反馈，会迅速引起T1导通，T2截止，Vc2输出高电平

• 问题：当输入从1降低时，什么时候电路的输出会发生变化？

• 要低到Ve+0.7
  

• 迅速转为T1截止T2导通，Vc2输出低电平

• 问题：输入为高电平和低电平时VT+和VT-为什么不一样？

• 因为+和-时Ve不同，虽然都是Ve+0.7
  

• 低电平没有前面电路那么低

器件实例

• 输出电路是一个推拉式的输出，想实现T4，T5导通输出低电平，T6导通输出高电平
• 再看电平偏移部分，当这部分给T4的输出至少是1.4V时，T4和T5才导通，输出低电平。T3的输出必须是高于2.8V（二极管的导通电压也是0.7V，四个PN结），才能让后面输出低电平，如果低于2.8V，T3，T4，T5都截止，输出高电平。所以这个电路就是把推拉输出的电平平移到了2.8V，起到了一个电平平移的作用
• 前面的二极管与门电路：下面四个二极管是保护电路，作用是输入电平比较低的时候保护，D1到D4就是一个与阵列
• 图形符号：
  
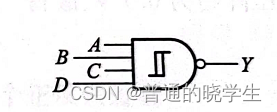
• 前面四个与是与阵列，取反是因为施密特出高电平，后面才输出0
• 四输出的与非门（只不过边沿特性比较好）
• 传输特性
  

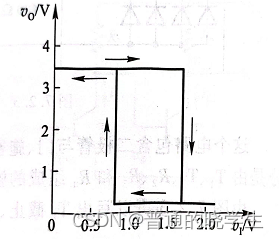
CMOS IC

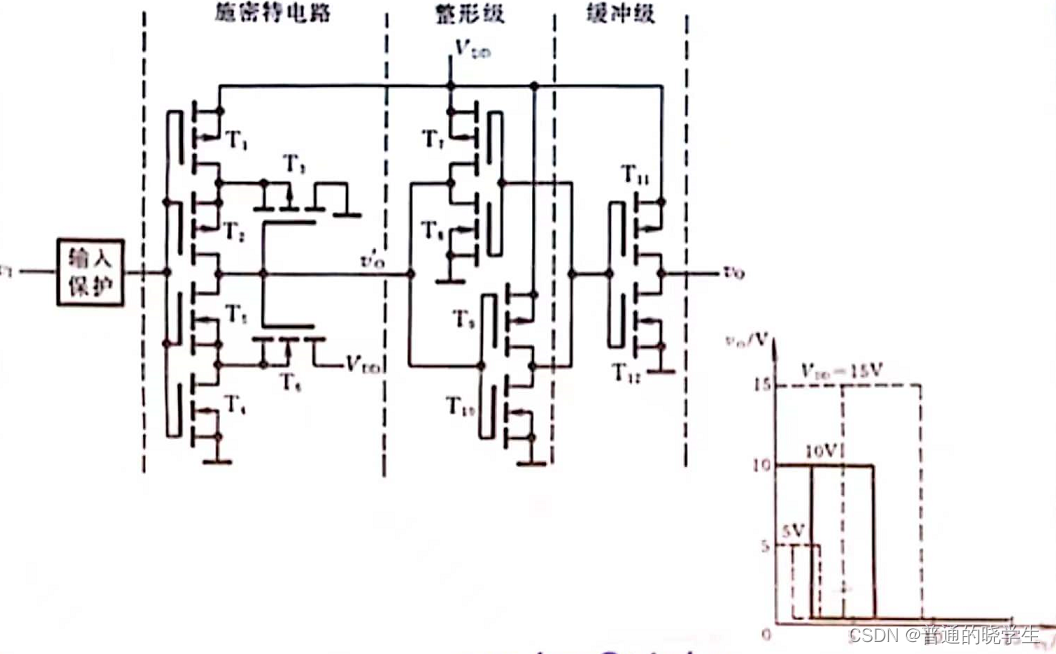
• 找出上升下降使得电路发生变化的们看电压

施密特触发器的特点

1. 输入信号在上升和下降过程中，电路状态转换的输入电平不同
2. 电路状态转换时有正反馈过程，使输出波形边沿变抖

施密特触发器的应用

1. 用于波形变换
   

2. 用于脉冲整形
   

3. 用于鉴幅
   

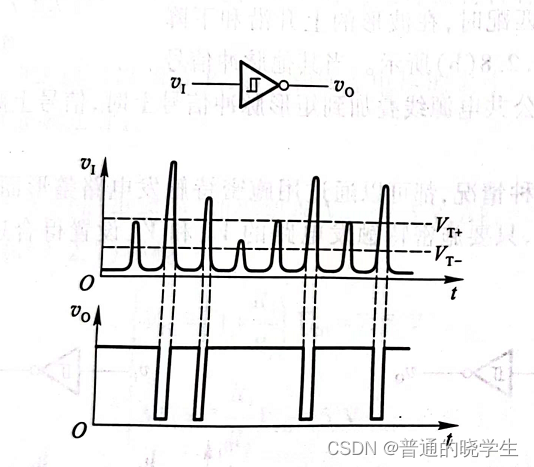
• 如果 要关心脉冲的宽度，可以把这个接到161（16进制计数器）上，用时钟源，把取反之后的i信号接到EP,ET上

单稳态触发器

场景举例：楼道灯，洗手

特点

1. 有一个稳态和一个暂稳态
2. 在外界触发信号作用下，能从稳态->暂稳态，维持一段时间后自动返回稳态
3. ！！！暂稳态维持的时间长短取决于电路的内部参数

用门电路组成的单稳态触发器

• 这章从这里开始把电容引进来，特点是要关注过渡过程

积分型

• TTL的门
• 问题：R不能太大，为什么？
• TTL电路有一个输入负载特性，也就是如果R太大的话，前面的低电平传不过来
• 工作过程分析：
  （1）稳态下：Vi = 0，Vo = 1，（Vo1 = Voh），Va = Voh（如果是稳态，Vi是0，Va也应该是高电平）
  （2）Vi上升后Vo=0，进入暂稳态，Vo1=0，C开始放电
  （3）当放至Va = Vth后，Vo=1，返回稳态
  （4）Vi下降后，C重新充电至Voh，恢复初始态

性能参数

• 画波形是这章分析电路的关键
• 拿到这个波形图，如果这是楼道里的灯，我第一个就把这个方案毙掉。因为触发不是一个边沿，是一个时间段，但是这个电路特别适合洗手池

输出脉宽

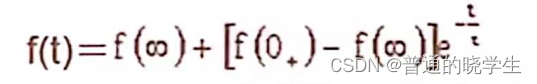
• 求脉冲宽度就应该跟据上面的公式，关心开始，终了还有时间常数

• 现在只需要直到时间常数就可以反推出t，公式如下
  

• 现在需要把电路打开了
  

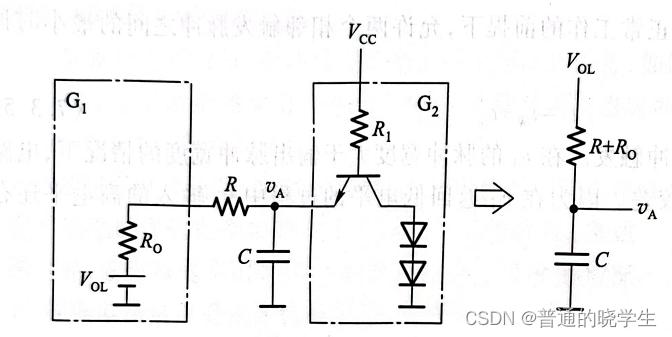
• 所有的门电路的输出都当作一个有内阻的电压源

• G2虽然画下来了，但是我关心的是Va的放电过程，那边没有放电回路，所以不用管它。等效成右边的电路就直到公式的R，C是多少

• 电容的过度过程一般需要3-5个时间常数就达到稳态
  

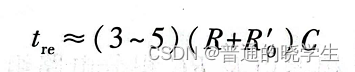
• 这个不需要精确计算，我就知道放完一次电之后，我经过多长时间就准备好为下一次充电了，这时候我要关心的值就是这次触发到下一次触发的间隔，所以最关键的还是Tw，是在暂稳态期间呆的时间

微分型

• 对前面的电路进行改进，目的是我不希望触发脉冲那么宽，希望找到一个适合楼道灯控制的这种类型的电路

• 工艺改用了CMOS工艺的门，Voh=Vdd，Vol = 0，Vth = 1/2Vdd
  

• 从电路图上，给出了两套RC。但是只有一套是和暂稳态相关的，是后面那套。

• 前面的电路是一个输入取微分电路

• 分析工作过程：
  （1）稳态下：Vi = 0，Vd = 0，Vi2 = Vdd，Vo = 0，（Vo1 = Vdd），C上无电压
  （2）Vi跳变到高电平，Vd跳变到高电平，Vo1跳变成低电平，Vi2跳变成低电平，Vo跳变成高电平，这时，就算Vi消失（消失后，Vd的电压会随着Cd放电变小），Vo的反馈也会保持暂稳态
  
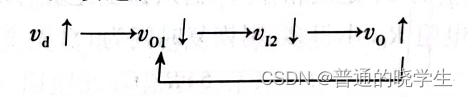
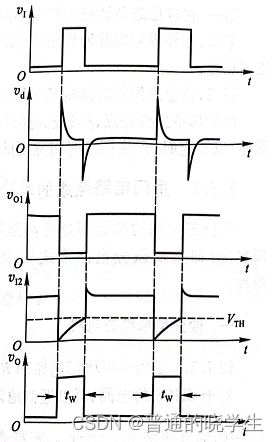
  （3）进入暂稳态之后，Vdd开始给C充电。开始充电后，Vi2的电压就会上升，直到Vth时，G2输出变成1了，反馈回G2，G1输出就变成1了，这时就会直接把Vi2拉高（基本回拉到Vth+Vdd，也就是3/2Vdd，能跳的原因就是电容两端的压差不突变），回到稳态
  

• 问题：但是从上图看，Vi2不会到3/2Vdd，为什么？

• 实际上，它是会跳到3/2Vdd的。但是因为用了CMOS工艺，输入上下端都有二极管保护（输入电平不能太高，不能高过Vdd+0.7，也不能太低，不能低过-0.7，因为一旦超过这个范围就会导通），所以，Vi2跳变的图应该这么画
  

• 这章，为了简化，不考虑这个变化，还是看上面的电平图，跳到Vdd+0.7

• 有了以上的分析，那么可以得出一个结论，输入的触发脉冲的宽度对输出的暂稳态不再有影响

• 刚刚的积分型电路，RC起的是积分的作用，缓慢放电。而这个电路的RC起的是微分的作用，进入暂稳态，直接耦合

性能参数计算 输出脉宽

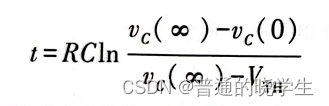
• 公式中唯一不确定的就是R，这时候打开电路
  
• 可以求得
  

集成的单稳态触发器

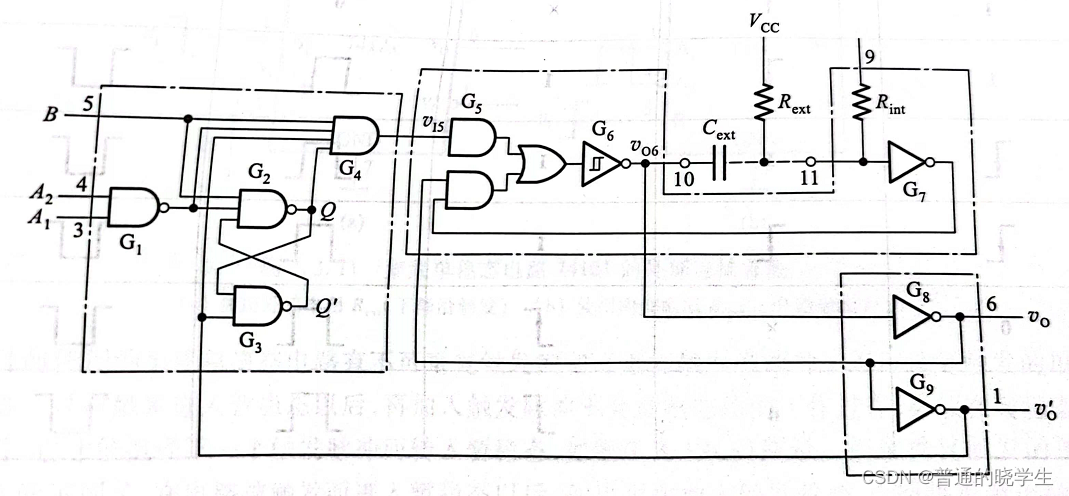
• 没有新的东西，就是把前面的单稳态触发电路当成一个核心，通过前面的门电路加了一个触发器
• 由于是集成的，提供了外接的RC
  
• 所以这时的计算就只能用RCln2
  
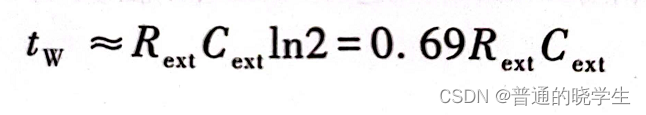
• ！！！引入一个概念，可重复触发
• 以灯为例，我跺脚让它亮，我感觉要灭的时候，我再跺脚，这时这个灯不会灭，而是会以我跺的第二脚作为暂稳态的时间起点
• ！！前面那两个电路进入暂稳态之后就屏蔽掉前面的触发信号了。而可重复出发指的是，进入暂稳态后，可以接着相应外部的触发信号，而且以最后一次触发的时间点，作为我暂稳态时间的起始点。
• ！！目前讲到的都不可以，因为积分型和微分型都是以电容上的过渡过程作为衡量器。而可重复触发指的是要随时随刻恢复到起始状态。