-
机器学习06|两万字:决策树 【jupyter代码详解篇】
本文用到的所有数据 机器学习06:决策树【代码及数据文件】
决策树(Decision Tree)首先对数据进行处理,利用归纳算法生成可读的规则和决策树,然后使用决策对新数据进行分析,本质上是通过一系列规则对数据进行分类的过程
决策树是一种典型的分类方法。其中:
- 每个内部结点表示一个属性上的判断
- 每个分支代表一个判断结果的输出
- 每个叶结点代表一种分类结果。
CLS算法是早期提出的决策树学习算法,是很多决策树学习算法的基础框架。
依据其中选择分类属性的策略不同,可以得到不同的决策树算法。比较常用的决策树有ID3,C4.5和CART三种和实现,其中CART一般优于其他决策树,并且可用于回归任务。下面我们将编写代码实现这三种决策树算法。
任务一: 导入包和创建数据集
本实验所需的包不多
- log用于计算
- treePlotter为已经编写好的用于可视化决策树的代码,createPlot(tree)就可以调用
- csv为对csv文件进行操作所需的包
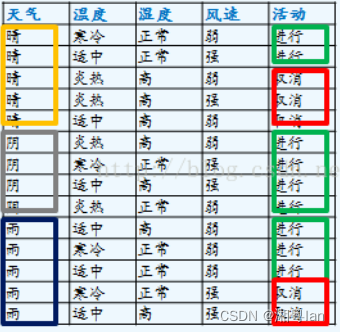
本实验第一个使用的是天气情况数据集,属性集合A={ 天气,温度,湿度,风速}, 类别标签有两个,类别集合L={进行(yes),取消(no)}。
本实验中我们用字典嵌套的形式来表示一个决策树,如一个形如
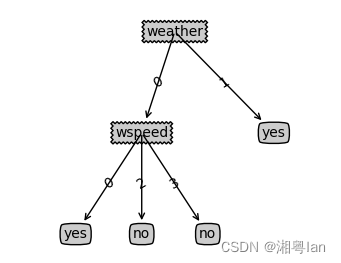
的决策树可表示为 {‘weather’: {0: {‘wspeed’: {0: ‘yes’, 2: ‘no’, 3: ‘no’}}, 1: ‘yes’}}
from math import log import treePlotter,csv import numpy as np def createDataSet1(): data=[ [0, 0, 0, 0, 'yes'], [0, 1, 0, 1, 'yes'], [0, 2, 1, 0, 'no'], [0, 2, 1, 1, 'no'], [0, 1, 1, 0, 'no'], [1, 2, 1, 0, 'yes'], [1, 0, 0, 1, 'yes'], [1, 1, 1, 1, 'yes'], [1, 2, 0, 0, 'yes'], [2, 1, 1, 0, 'yes'], [2, 0, 0, 0, 'yes'], [2, 1, 0, 0, 'yes'], [2, 0, 0, 1, 'no'], [2, 1, 1, 1, 'no'] ] features=['weather','temperature','humidity','wspeed'] return data,features data1,features1 = createDataSet1() features1- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
['weather', 'temperature', 'humidity', 'wspeed']- 1
任务二:ID3树
ID3 以信息熵的增益来作为分类的依据。假设样本集D中第 k k k类样本占比 p k p_k pk,可计算其对应信息熵为: E n t ( D ) = − ∑ k p k l o g p k Ent(D)=-\sum_k p_k log p_k Ent(D)=−k∑pklogpk E n t ( D ) Ent(D) Ent(D)越小,代表数据集越有序,纯度越高。我们首先编写计算数据集香农熵的函数。
2.1完成香农熵计算函数
def calcShannonEnt(dataSet): """ 函数:计算数据集香农熵 参数:dataSet:数据集 labels:数据标签 返回:shannonEnt 数据集对应的香农熵 """ numEntries = len(dataSet) #样本数 labelCounts = {} #统计不同label出现次数的字典(key为label,value为出现次数) shannonEnt = 0.0 #计算labelCounts for featVec in dataSet: # 获取当前这条数据的label值 currentLabel = featVec[-1] # 是新label,则在标签字典中新建对应的key,value的对应出现的次数,初始化为0 # 已有则当前label出现次数+1 labelCounts[currentLabel] = labelCounts.get(currentLabel,0) + 1 ### START CODE HERE ### pk={} for key in labelCounts: pk[key] = labelCounts[key]/numEntries shannonEnt = shannonEnt - pk[key] * log(pk[key],2) ### END CODE HERE ### return shannonEnt- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 1
print(calcShannonEnt(data1)) data1[0][-1] = 'maybe' #尝试增加一个分类选项,观察熵变化 print(calcShannonEnt(data1)) data1[0][-1] = 'yes' #还原- 1
- 2
- 3
- 4
0.9402859586706309 1.2638091738835462- 1
- 2
2.2 完成基本功能函数
- splitDataSet:用于在决策树每个分支,将特征取某个值的所有数据划分为一个数据集
def splitDataSet(dataSet, axis, value): """ 函数:将axis列属性值为value的组合为一个数据集,并删除第axis列特征信息 参数:axis:特征列索引 value:待分离的特征取值 返回:retDataSet:被分割出来的数据集 """ retDataSet = [] for data in dataSet: # 如果数据集的第axis列值等于value,保留条数据,并删除第axis列特征信息 if data[axis] == value: # 获取被降维特征前面的所有特征 reducedFeatVec = data[:axis] # 接上被降维特征后面的所有特征 reducedFeatVec.extend(data[axis + 1:]) # 新的降维数据加入新的返回数据集中 retDataSet.append(reducedFeatVec) return retDataSet splitDataSet(data1,0,1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
[[2, 1, 0, 'yes'], [0, 0, 1, 'yes'], [1, 1, 1, 'yes'], [2, 0, 0, 'yes']]- 1
2.3 用信息增益选择待分类的特征
那么假设用离散属性a有V个可能值,划分能产生V个分支,每个分支包含的数据记为 D v D^v Dv。
由此我们可以得出用属性a对样本集D划分的信息增益计算公式:
G a i n ( D , a ) = E n t ( D ) − ∑ v ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a)=Ent(D)-\sum_v\frac{|D^v|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v∑∣D∣∣Dv∣Ent(Dv)def chooseBestFeature_ID3(dataSet): """ 函数:利用香农熵,计算所有可能划分的信息增益,输出当前数据集最好的分类特征 参数:dataSet 返回:bestFeature:最优特征的index(下标) """ numFeatures = len(dataSet[0]) - 1 #特征数 baseEntropy = calcShannonEnt(dataSet) #Ent(D) bestInfoGain = 0.0 #信息增益 bestFeature = -1 #最好信息增益特征 #遍历每个特征 for i in range(numFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) #第i个特征的可能取值 newEntropy = 0.0 ### START CODE HERE ### splitData = {} #存放每一个可能取值的所有数据 #计算以第i个特征划分产生的infoGain for j in uniqueVals: splitData[j] = splitDataSet(dataSet,i,j) newEntropy = newEntropy + calcShannonEnt(splitData[j]) * (len(splitData[j])/len(dataSet)) #计算此特征下的Gain后半累加的部分。 infoGain = baseEntropy - newEntropy #如果大于当前bestInfoGain,则保留当前划分为最优划分 if infoGain > bestInfoGain: bestInfoGain = infoGain bestFeature = i ### END CODE HERE ### return bestFeature chooseBestFeature_ID3(data1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
0- 1
numFeatures=len(data1[0])-1 for i in range(numFeatures): featList = [example[i] for example in data1] print(featList) for example in data1: print(example) data1,len(data1)- 1
- 2
- 3
- 4
- 5
- 6
- 7
[0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2] [0, 1, 2, 2, 1, 2, 0, 1, 2, 1, 0, 1, 0, 1] [0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1] [0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1] [0, 0, 0, 0, 'yes'] [0, 1, 0, 1, 'yes'] [0, 2, 1, 0, 'no'] [0, 2, 1, 1, 'no'] [0, 1, 1, 0, 'no'] [1, 2, 1, 0, 'yes'] [1, 0, 0, 1, 'yes'] [1, 1, 1, 1, 'yes'] [1, 2, 0, 0, 'yes'] [2, 1, 1, 0, 'yes'] [2, 0, 0, 0, 'yes'] [2, 1, 0, 0, 'yes'] [2, 0, 0, 1, 'no'] [2, 1, 1, 1, 'no'] ([[0, 0, 0, 0, 'yes'], [0, 1, 0, 1, 'yes'], [0, 2, 1, 0, 'no'], [0, 2, 1, 1, 'no'], [0, 1, 1, 0, 'no'], [1, 2, 1, 0, 'yes'], [1, 0, 0, 1, 'yes'], [1, 1, 1, 1, 'yes'], [1, 2, 0, 0, 'yes'], [2, 1, 1, 0, 'yes'], [2, 0, 0, 0, 'yes'], [2, 1, 0, 0, 'yes'], [2, 0, 0, 1, 'no'], [2, 1, 1, 1, 'no']], 14)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
2.4 生成ID3决策树
接下来我们可以用 递归 的方法生成决策树,其基本流程如下:
- 划分条件:自根结点开始,通过选择出最佳属性进行划分树结构,并递归划分;
- 停止条件:当前结点都是同一种类型;当前结点后为空,或者所有样本在所有属性上取值相同,无法划分;
这是通用的创建决策树的函数,根据参数chooseBestFeature的不同,得到不同算法的决策树,当前任务中参数为刚刚编写的 chooseBestFeature_ID3。
备注:
此处代码实现的ID3树,每个结点不能选取祖先结点用过的分类特征。
而实际上结点的不同子树,是有可能选取同样的分类特征的。
原因在于代码实现的 del (features[bestFeat]) 会导致一个特征被选用后,之后就再不能被选用。可以通过在递归时传入features的一份复制来避免这个问题。def majorityCnt(classList): """ 函数:计算占比最大的分类标签 参数:classList分类标签 返回:占比最大的分类标签 """ classCount={} for vote in classList: if vote not in classCount.keys(): classCount[vote]=0 classCount[vote]+=1 return max(classCount, key=classCount.get)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
def createTree(dataSet, features, chooseBestFeature): """ 函数:递归地根据数据集和数据特征名创建决策树 参数:chooseBestFeature:函数作为参数,通过chooseBestFeature(dataSet)调用, 根据参数的不同,获取由ID3或C4.5算法选择的最优特征的index 返回:myTree:由集合表示的决策树 """ classList = [data[-1] for data in dataSet] #当前数据集的所有标签 bestFeat = chooseBestFeature(dataSet) #当前数据集最优特征,划分数据集合,计算出最好的划分数据集特征 bestFeatName = features[bestFeat] #最优特征的标签名 myTree = {bestFeatName: {}} #构造当前结点——最优特征:子结点集合 del(features[bestFeat]) #删除已用过的分类标签 ### START CODE HERE ### # 如果当前dataSet所有的标签相同,此结点分类完毕,结束决策,返回分类标签 if classList.count(classList[0]) == len(classList): return classList[0] # 如果当前dataSet无特征,此结点分类完毕,结束决策,返回占比最大的分类标签 if len(dataSet[0]) == 1: # 由于无法返回唯一的类标签,使用majorityCnt取得最多频率的标签 return majorityCnt(classList) # 否则,为每个最优特征取值,递归地创建子树 #字典类型存储树的信息 myTree = {bestFeatName: {}} featValues = [example[bestFeat] for example in dataSet] #set() 函数创建一个无序不重复元素集,可进行关系测试,删除重复数据,还可以计算交集、差集、并集等。 #构成了一个不重复的属性值集合 uniqueVals = set(featValues) # 遍历这个不重复的属性集合, for value in uniqueVals: #subLabels 就是features去掉列表包含属性值的后的标签列表 #为了保证每次调用函数createTree() 时不改变原始列表的内容,使用新变量subLabels 代替原始列表 subLabels = features[:] # bestFeatName=列表中最好数据的集合的值 value=不重复的标签 # 得到的返回值将被插入到字典变量myTree 中 myTree[bestFeatName][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels,chooseBestFeature) ### END CODE HERE ### return myTree data1, labels1 = createDataSet1() ID3Tree = createTree(data1, labels1,chooseBestFeature_ID3) treePlotter.createPlot(ID3Tree)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
Sample Output: 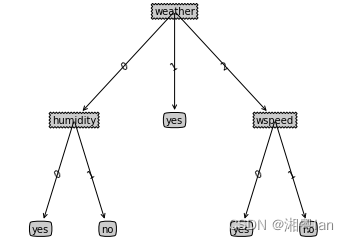
任务三:C4.5树
ID3用信息增益选择属性的方式会让他对取值数目较多的属性产生偏好,接下来我们通过一个直观的例子来说明。
假设数据集变成如下所示,某个属性(如风速)变为每个样本一个值的情况,构建一个ID3树。
def createDataSet2(): data=[ [0, 0, 1, 0, 'yes'], [1, 1, 0, 1, 'yes'], [0, 0, 0, 2, 'no'], [0, 1, 1, 3, 'no'], [1, 1, 1, 4, 'yes'] ] features2=['weather','temperature','humidity','wspeed'] return data,features2 data2, features2 = createDataSet2() ID3Tree = createTree(data2, features2, chooseBestFeature_ID3) treePlotter.createPlot(ID3Tree)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
Sample Output: 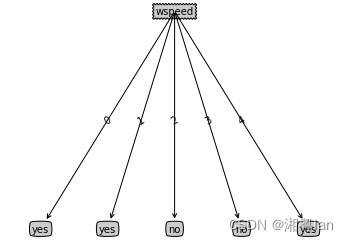
可以观察到,ID3树利用了该属性为每一个样本创建了分支,这样得到的决策树显然泛化性会很差。
为了进行改进,我们可以设想为信息增益增加一个类似于正则项的惩罚参数,在特征取值多时,降低信息增益。信息增益比 = 惩罚参数 * 信息增益
C4.5算法为属性定义一个Intrinsic Value(IV)来构建这个惩罚参数: I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g ∣ D v ∣ ∣ D ∣ IV(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|}log\frac{|D^v|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log∣D∣∣Dv∣
其数学意义为:以特征a作为随机变量的熵的倒数。假设某个属性将样本等分为x份,可得其 I V = − l o g ( 1 / x ) IV=-log(1/x) IV=−log(1/x)
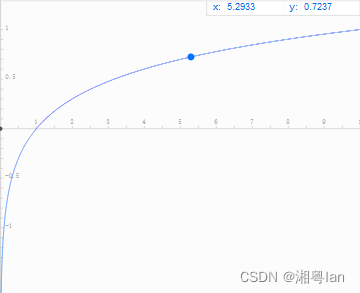
观察函数图像会发现,样本划分越多,x越大,其值越大
于是可将信息增益改进为信息增益比 G a i n R a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) GainRatio(D,a)=\frac{Gain(D,a)}{IV(a)} GainRatio(D,a)=IV(a)Gain(D,a)
任务3.1 用信息增益比选择分类特征
def chooseBestFeature_C45(dataSet): """ 函数:计算所有可能划分的信息增益比,输出当前数据集最好的分类特征 参数:dataSet 返回:bestFeature:最优特征的index(下标) """ numFeatures = len(dataSet[0]) - 1 baseEntropy = calcShannonEnt(dataSet) bestInfoGain = 0.0 bestFeature = -1 for i in range(numFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) newEntropy = 0.0 IV = 0.0 ### START CODE HERE ### splitData = {} #存放每一个可能取值的所有数据 # 计算以第i个特征划分的infoGain,以及其IV # 注意IV=0时直接continue,可以思考一下什么情况会使IV=0 for value in uniqueVals: splitData[value] = splitDataSet(dataSet,i,value) ratio = (len(splitData[value])/len(dataSet)) newEntropy = newEntropy + calcShannonEnt(splitData[value])*ratio #计算此特征下的Gain后半累加的部分。 IV = IV - ratio*log(ratio,2) infoGain = baseEntropy - newEntropy #一个训练样本在某一属性下的信息增益 if(IV==0): continue # 计算GainRatio衰减 GainRatio = infoGain/IV # 如果大于当前最优,则保留当前划分为最优划分 if (GainRatio > bestInfoGain): bestInfoGain = GainRatio bestFeature = i ### END CODE HERE ### return bestFeature- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
任务3.2 生成C4.5树
data2, labels2 = createDataSet2() C45Tree = createTree(data2, labels2, chooseBestFeature_C45) treePlotter.createPlot(C45Tree)- 1
- 2
- 3
Sample Output: 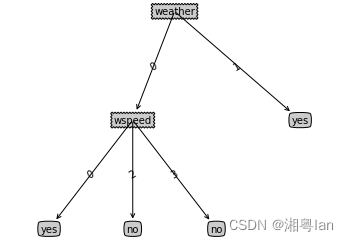
可以观察到,C4.5算法的确对特征取值较少的属性产生了更多偏好,可以有效的避免上述ID3树存在的问题。但C4.5算法分类结果还是存在一定的过拟合。
任务四:剪枝
在决策树学习的过程中,为了尽量正确分类训练样本,节点划分过程将不断重复,有时会造成决策树分支过多,这时就可能因为训练样本学得太好导致“过拟合”,剪枝是决策树学习算法应对“过拟合”的主要手段。
决策树剪枝的基本策略有“预剪枝”和“后剪枝”。预剪枝是指在决策树生成的过程中,对每个结点在划分前进行估计,若当前结点的划分不能带来决策树泛化性能的提升,则停止划分并将当前结点标记为叶结点;后剪枝是指从训练集生成一颗完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换成叶结点能带来泛化性能的提升,则将该结点替换为叶子结点。
这里我们将实现对ID3决策树进行“预剪枝”
def createDataSet3(): data=[ [1, 2, 1, 0, 2, 0, 'yes'], [2, 2, 2, 0, 2, 0, 'yes'], [2, 2, 1, 0, 2, 0, 'yes'], [1, 1, 1, 0, 1, 1, 'yes'], [2, 1, 1, 1, 1, 1, 'yes'], [1, 0, 0, 0, 0, 1, 'no'], [0, 1, 2, 1, 2, 0, 'no'], [2, 1, 1, 0, 1, 1, 'no'], [0, 2, 1, 2, 0, 0, 'no'], [1, 2, 2, 1, 1, 0, 'no'] ] testdata=[ [1, 2, 2, 0, 2, 0, 'yes'], [0, 2, 1, 0, 2, 0, 'yes'], [2, 1, 1, 0, 1, 0, 'yes'], [2, 0, 2, 1, 1, 0, 'no'], [0, 0, 0, 2, 0, 0, 'no'], [0, 2, 1, 2, 0, 1, 'no'], [1, 1, 1, 1, 2, 0, 'no'] ] features3=['coat','trousers','hat','shoes','shirt','scarf'] return data,testdata,features3 data3, testdata, features3 = createDataSet3() ID3Tree = createTree(data3, features3, chooseBestFeature_ID3) treePlotter.createPlot(ID3Tree)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
Sample Output: 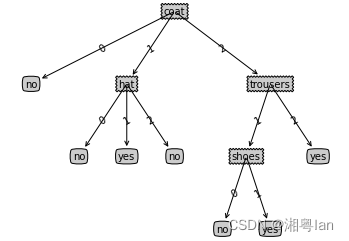
未剪枝决策树示例
def testingMajor(major, data_test): """ 函数:计算不保留子树造成的错误数量 参数:data_test,major:占比最大的分类标签 返回:错误数量 """ error = 0.0 for i in range(len(data_test)): if major != data_test[i][-1]: error += 1 return float(error)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
def testing_feat(bestFeatIndex, train_data, test_data, labels): """ 函数:计算保留子树造成的错误数量 参数:bestFeatIndex:最优特征的index(下标),train_data:训练数据集, test_data:测试数据集, labels:数据标签 返回:错误数量 """ class_list = [example[-1] for example in train_data] train_data = [example[bestFeatIndex] for example in train_data] test_data = [(example[bestFeatIndex], example[-1]) for example in test_data] all_feat = set(train_data) error = 0.0 for value in all_feat: class_feat = [class_list[i] for i in range(len(class_list)) if train_data[i] == value] major = majorityCnt(class_feat) for data in test_data: if data[0] == value and data[1] != major: error += 1.0 return error- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
def createTree_prune(dataSet,labels,test_data,chooseBestFeature,mode='prev'): """ 函数:递归地根据数据集和数据特征名创建预剪枝决策树 参数:dataSet:训练数据集,labels:数据标签,test_data:测试数据集,chooseBestFeature:函数作为参数,通过chooseBestFeature(dataSet)调用, 根据参数的不同,获取由ID3或C4.5算法选择的最优特征的index 返回:myTree:由集合表示的决策树 """ classList=[example[-1] for example in dataSet] # dataSet指的是当前的数据集,不是最初的数据集 # classList指的是当前数据集的所有标签(不去重) #下面是递归截止条件 if classList.count(classList[0])==len(classList):#这个意思是如果当前数据集中的所有数据都属于同一个类别 return classList[0] if len(dataSet[0])==1: return majorityCnt(classList) #选择最佳分割特征 labels_copy = labels #labels_copy = copy.deepcopy(labels)#深拷贝就是:labels_copy和lables撇清关系 bestFeat=chooseBestFeature(dataSet) bestFeatLabel=labels[bestFeat] if mode == "prev": ### START CODE HERE ### #如果剪枝前的错误数量小于剪枝后的错误数量,那么就保留该子树 if (testing_feat(bestFeat, dataSet, test_data, labels_copy) > testingMajor(majorityCnt(classList),test_data)): return majorityCnt(classList) ### END CODE HERE ### myTree = {bestFeatLabel: {}} featValues=[example[bestFeat] for example in dataSet] uniqueVals=set(featValues) #uniqueVals用来获得当前数据集的最佳分割属性剩余的取值有哪些 del (labels[bestFeat])#删除根节点的已经用过的特征 for value in uniqueVals: subLabels = labels[:] myTree[bestFeatLabel][value] = createTree_prune(splitDataSet(dataSet, bestFeat, value), subLabels,splitDataSet(test_data, bestFeat, value),chooseBestFeature, mode=mode) return myTree- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
data3, testdata, features3 = createDataSet3() MyTree = createTree_prune(data3, features3, testdata, chooseBestFeature_ID3) treePlotter.createPlot(MyTree)- 1
- 2
- 3
Sample Output: 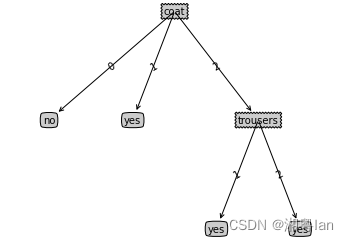
任务五:CART
前面的实验我们发现ID3和C4.5算法在用于分类问题是有效的,那么决策树可以适用于回归问题吗?
CART(Classification and regression tree)如其名,便是可以既可以用于解决分类问题,又可以用于解决回归问题的决策树算法。
在解决分类问题时:
ID3/C4.5基于信息论熵模型选择一个离散的特征进行分类,根据特征取值数目一次性划分若干子结点,然后子结点的数据集将不再包含这个特征,这个特征不再参与接下来的分类,这意味着这种决策树模型是不能直接处理连续取值的特征的,除非划分区间将其离散化。
CART则根据基尼系数(Gini Index) 为连续或离散的特征选择一个划分点,产生左右两个分支,生成二叉树。在产生分支后,仍可以再利用这个特征,参与接下来的分类,产生下一个分支。用叶子结点样本最多的标签作为预测输出。
在解决回归问题时:
CART根据平方损失选择最优划分特征和划分点,并用叶子结点样本标签均值作为预测输出。
接下来我们来具体实现CART回归树,并尝试用于解决一个分类问题。
任务5.1 iris数据集读取和预处理
Iris数据集即鸢尾属植物数据集,该数据集测量了所有150个样本的4个特征,分别是:
- sepal length(花萼长度)
- sepal width(花萼宽度)
- petal length(花瓣长度)
- petal width(花瓣宽度)
标签为其种属:Iris Setosa,Iris Versicolour,Iris Virginica。该数据集被广泛用于分类算法示例,我们可以看到其4个特征取值均是连续的。数据集存储在 iris.csv 文件中,我们从中手动划分一部分作为训练集。
def createDataSetIris(): ''' 函数:获取鸢尾花数据集,以及预处理 返回: Data:构建决策树的数据集(因打乱有一定随机性) Data_test:手动划分的测试集 featrues:特征名列表 labels:标签名列表 ''' labels = ["setosa","versicolor","virginica"] with open('iris.csv','r') as f: rawData = np.array(list(csv.reader(f))) features = np.array(rawData[0,1:-1]) dataSet = np.array(rawData[1:,1:]) #去除序号和特征列 np.random.shuffle(dataSet) #打乱(之前如果不加array()得到的会是引用,rawData会被一并打乱) return rawData[1:,1:], dataSet, features, labels rawData, data, features, labels = createDataSetIris() print(rawData[0]) print(data[0]) print(features) print(labels)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
['5.1' '3.5' '1.4' '0.2' 'setosa'] ['5' '3.3' '1.4' '0.2' 'setosa'] ['Sepal.Length' 'Sepal.Width' 'Petal.Length' 'Petal.Width'] ['setosa', 'versicolor', 'virginica']- 1
- 2
- 3
- 4
5.2 完成基尼指数计算函数
数据集D的基尼值(Gini Index)计算公式如下:
G i n i ( D ) = ∑ k = 1 K ∑ k ′ ≠ K p k p k ′ = 1 − ∑ k = 1 K p k 2 Gini(D)=\sum_{k=1}^{K}\sum_{k'≠K}p_kp_k'=1-\sum_{k=1}^{K}p_k^2 Gini(D)=k=1∑Kk′=K∑pkpk′=1−k=1∑Kpk2
其数学意义为,从数据集中任选两个样本,类别不一致的概率。其值越小,数据集纯度越高。数据集D某个划分a的基尼系数计算如下:
G i n i I n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) GiniIndex(D,a)=\sum_{v=1}^{V}\frac{|D^v|}{|D|}Gini(D^v) GiniIndex(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)def calcGiniIndex(dataSet): ''' 函数:计算数据集基尼值 参数:dataSet:数据集 返回: Gini值 ''' counts = [] #每个标签在数据集中出现的次数 count = len(dataSet) #数据集长度 for label in labels: counts.append([d[-1] == label for d in dataSet].count(True)) ### START CODE HERE ### Gini = 0.0 GiniIndex = 0.0 for label in range(len(labels)): Gini =1 - (counts[label]/count)**2 GiniIndex = GiniIndex + Gini*(counts[label]/count) ### END CODE HERE ### return GiniIndex calcGiniIndex(rawData)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
0.8888888888888888- 1
5.3 完成基本功能函数
- binarySplitDataSet: 和ID3,C4.5不同,CART每个划分均为二分,且不删除特征信息。这里由于已知数据集特征取值全是连续取值型的, 对算法的部分功能进行了并不严谨的简化。实际应用中的CART还应该判断特征取值是否离散,若离散,并把feature等于和不等于value的数据划分为两个数据集。
- classificationLeaf:用于分类命题,此处实现的是多数表决器,叶结点输出数据集最多的标签作为分类。如果是用于回归问题,叶结点应该输出的是数据集列的均值作为回归预测。
def binarySplitDataSet(dataSet, feature, value): ''' 函数:将数据集按特征列的某一取值换分为左右两个子数据集 参数:dataSet:数据集 feature:数据集中某一特征列 value:该特征列中的某个取值 返回:左右子数据集 ''' matLeft = np.array([d for d in dataSet if d[feature] <= value]) matRight = np.array([d for d in dataSet if d[feature] > value]) return matLeft,matRight binarySplitDataSet(rawData,0,"4.7")[0]- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
array([['4.7', '3.2', '1.3', '0.2', 'setosa'], ['4.6', '3.1', '1.5', '0.2', 'setosa'], ['4.6', '3.4', '1.4', '0.3', 'setosa'], ['4.4', '2.9', '1.4', '0.2', 'setosa'], ['4.3', '3', '1.1', '0.1', 'setosa'], ['4.6', '3.6', '1', '0.2', 'setosa'], ['4.7', '3.2', '1.6', '0.2', 'setosa'], ['4.4', '3', '1.3', '0.2', 'setosa'], ['4.5', '2.3', '1.3', '0.3', 'setosa'], ['4.4', '3.2', '1.3', '0.2', 'setosa'], ['4.6', '3.2', '1.4', '0.2', 'setosa']], dtype='- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
def classifyLeaf(dataSet, labels): ''' 函数:求数据集最多的标签,用于结点分类 参数:dataSet:数据集 labels:标签名列表 返回:该标签的index ''' counts = [] for label in labels: counts.append([d[-1] == label for d in dataSet].count(True)) return np.argmax(counts) #argmax:使counts取最大值的下标 classifyLeaf(rawData[40:120],labels)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
1- 1
5.4 用基尼系数选择特征及划分点
CART在这一步选择的不仅是特征,而是特征以及该特征的一个分界点。CART要遍历所有特征的所有样本取值作为分界点的Gini系数,从中找出最优特征和最优划分。
在这里我们进一步地为决策树设定停止条件——阈值。当结点样本树足够小或者Gini增益足够小的时候停止划分,将结点中最多的样本作为结点的决策分类。
def chooseBestSplit(dataSet, labels, leafType=classifyLeaf, errType=calcGiniIndex, threshold=(0.01,7)): ''' 函数:利用基尼系数选择最佳划分特征及相应的划分点 参数:dataSet:数据集 leafType:叶结点输出函数(当前实验为分类) errType:损失函数,选择划分的依据(分类问题用的就是GiniIndex) threshold: Gini阈值,样本阈值(结点Gini或样本数低于阈值时停止) 返回:bestFeatureIndex:划分特征 bestFeatureValue:最优特征划分点 ''' thresholdErr = threshold[0] #Gini阈值 thresholdSamples = threshold[1] #样本阈值 err = errType(dataSet) bestErr = np.inf bestFeatureIndex = 0 #最优特征的index bestFeatureValue = 0 #最优特征划分点 ### START CODE HERE ### #当数据中输出值都相等时,返回叶结点(即feature=None,value=结点分类) if len(set(dataSet[:,-1].T.tolist()[0])) == 1: #分完了,没有属性了 return None, leafType(dataSet,labels) #少数服从多数,返回训练样本数最多的类别作为叶节点 #尝试所有特征的所有取值,二分数据集,计算err(本实验为Gini),保留bestErr m,n = np.shape(dataSet) for featIndex in range(n - 1): for splitVal in set(dataSet[:,featIndex]): mat0, mat1 = binarySplitDataSet(dataSet, featIndex, splitVal) if (np.shape(mat0)[0] < thresholdSamples) or (np.shape(mat1)[0] < thresholdSamples): continue newS = errType(mat0) + errType(mat1) if newS < bestErr: bestFeatureIndex = featIndex bestFeatureValue = splitVal bestErr = newS #检验Gini阈值,若是则不再划分,返回叶结点 if (err - bestErr) < thresholdErr: return None, leafType(dataSet,labels) #如果过误差减少不大则退出 #检验左右数据集的样本数是否小于阈值,若是则不再划分,返回叶结点 mat0, mat1 = binarySplitDataSet(dataSet, bestFeatureIndex, bestFeatureValue) if (np.shape(mat0)[0] < thresholdSamples) or (np.shape(mat1)[0] < thresholdSamples): #exit cond 3 return None, leafType(dataSet,labels) ### END CODE HERE ### return bestFeatureIndex,bestFeatureValue chooseBestSplit(rawData, labels)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
(2, '1.9')- 1
5.5 生成CART
根据参数leafType,errType的不同,生成CART分类树或是CART回归树。
def createTree_CART(dataSet, labels, leafType=classifyLeaf, errType=calcGiniIndex, threshold=(0.01,7)): ''' 函数:建立CART树 参数:dataSet:数据集 leafType:叶结点输出函数(当前实验为分类) errType:损失函数,选择划分的依据(分类问题用的就是GiniIndex) threshold: Gini阈值,样本阈值(结点Gini或样本数低于阈值时停止) 返回:CART树 ''' feature,value = chooseBestSplit(dataSet, labels, leafType, errType, threshold) ### START CODE HERE ### #是叶结点则返回决策分类(chooseBestSplit返回None时表明这里是叶结点) if feature == None: return labels[leafType(dataSet, labels)] #否则创建分支,递归生成子树 bestFeatureName = features[feature] leftTree, rightTree = binarySplitDataSet(dataSet, feature, value) ### END CODE HERE ### myTree = {bestFeatureName: { f'<={value} contains{len(leftTree)}': createTree_CART(leftTree, labels, leafType, errType, threshold), f'>{value} contains{len(rightTree)}': createTree_CART(rightTree, labels, leafType, errType, threshold)}} return myTree ### END CODE HERE ### return myTree CARTTree = createTree_CART(data, labels, classifyLeaf, calcGiniIndex, (0.01,7)) treePlotter.createPlot(CARTTree)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
Sample Output: 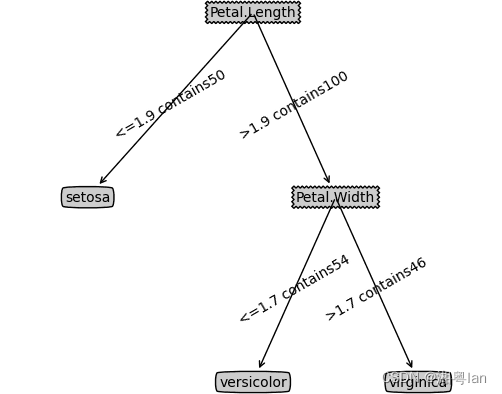
备注:
- 由于实现细节,实现顺序有所不同,最终生成的树可能也不一样,之前函数的测试样例通过即可。
- 一个分支两个子结点分类相同是未达到Gini阈值,却达到样本阈值导致的,可以通过更改特征选择代码中,停止划分判断的顺序避免。
从实例可以看到一些CART树的特点,如:连续属性二分划分特征,特征可重复用于结点分类等等
jQuery使用echarts循环插入图表
【前端工程化】经验总结
Linux 环境部署
Day01 SpringBoot第一次笔记---运维实用篇
短视频平台如何保证内容安全问题?
网站出现403 Forbidden错误的原因以及怎么解决的方法
doris 动态分区
93. 复原 IP 地址
12.Oracle的索引
