wy的leetcode刷题记录_Day32

wy的leetcode刷题记录_Day32

时间：2022-11-3

1668. 最大重复子字符串

今天的每日一题是：1668. 最大重复子字符串

题目介绍

给你一个字符串 sequence ，如果字符串 word 连续重复 k 次形成的字符串sequence 的一个子字符串，那么单词 word 的 重复值为 k 。单词 word 的 最大重复值 是单词 word 在 sequence 中最大的重复值。如果 word 不是 sequence 的子串，那么重复值 k 为 0 。
给你一个字符串 sequence 和 word ，请你返回 最大重复值 k 。

示例 1：
输入：sequence = “ababc”, word = “ab”
输出：2
解释：“abab” 是 "ababc"的子字符串。

示例 2：
输入：sequence = “ababc”, word = “ba”
输出：1
解释：“ba” 是 "ababc"的子字符串，但 “baba” 不是 “ababc” 的子字符串。

思路

思路一：爆搜+动态规划：遍历sequence如果word的与此时的index相等那么就记录对应成功

1. 确定dp数组的含义：dp[i]表示到下表i时最大的重复子字符串的个数
2. 确定dp数组的递推公式：每当一个word.size()大小的滑动窗口匹配成功，那么他就在遍历到此时sequence的下表i前word.size()位，即i-word.size()时的最大重复子字符串加1。

if(flag)
{
	dp[i]=(i==m-1?0:dp[i-m])+1;
}
1
2
3
4

3. 初始化：同上块代码，如果第一个滑动窗口就匹配的话就把他初始化为0，其他也初始化为0；

思路二：KMP+动态规划：动态规划的定义如上一样；这里主要讲一下KMP，上述的暴搜方法是建立在字符串长度较小的情况下，如果字符串长度过大则会导致搜索时间过长而超时，对于上述每一次遍历就回到sequence的下一个字符的方法中我们改进为跳设比较不成功的位数为i，word比较位跳转到next[i]位sequence继续下一位比较。而这个next数组是kmp的关键，我们在一开始要建立这个next数组，他表示的含义是一个前缀函数：此时已经匹配i-1位的word后缀与word前缀的前next[i]位是一致的。接下来只需要用word的前next[i]位继续去匹配这个没有成功的i位。不需要再用word[0]继续去匹配了。

代码

class Solution {
public:
    int maxRepeating(string sequence, string word) {
        int n=sequence.size();
        int m=word.size();
        int ans=0;
        vector<int> dp(n);

        for(int i=m-1;i<n;i++)//注意题目不算之前符合条件的子字符串
        {
            bool flag=true;
            for(int j=0;j<m;j++)
            {
                if(word[j]!=sequence[i-m+1+j])
                {
                    flag=false;
                  //  temp=0;
                }
                if(!flag)
                    break;
            }
            if(flag)
            {
                dp[i]=(i==m-1?0:dp[i-m])+1;
            }
        }
        ans=*max_element(dp.begin(),dp.end());
        return ans;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
public:
    int maxRepeating(string sequence, string word) {
        int n = sequence.size(), m = word.size();
        if (n < m) {
            return 0;
        }

        vector<int> next(m, -1);
        for (int i = 1; i < m; ++i) {
            int j = next[i - 1];
            while (j != -1 && word[j + 1] != word[i]) {
                j = next[j];
            }
            if (word[j + 1] == word[i]) {
                next[i] = j + 1;
            }
        }

        vector<int> dp(n);
        int j = -1;
        for (int i = 0; i < n; ++i) {
            while (j != -1 && word[j + 1] != sequence[i]) {
                j = next[j];
            }
            if (word[j + 1] == sequence[i]) {
                ++j;
                if (j == m - 1) {
                    dp[i] = (i >= m ? dp[i - m] : 0) + 1;
                    j = next[j];
                }
            }
        }

        return *max_element(dp.begin(), dp.end());
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

收获

重新了解了KMP算法的知识，对字符串匹配的题目有了新的认识，使用KMP算法能大大缩短时间，但是不太好理解，就好似一个不固定长度的滑动窗口（但是他是事先预定好的，通过对比字符串算出next数组，只是在匹配时遇到的不匹配位数不一样罢了）。

637. 二叉树的层平均值

637. 二叉树的层平均值

题目介绍

• 给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1：

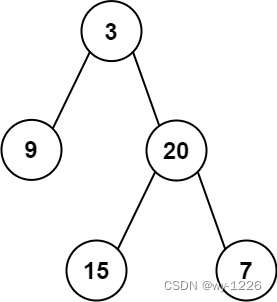
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。 因此返回 [3, 14.5, 11] 。

示例 2:

输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

思路

方法一：BFS：老样子层序遍历然后记录每一层的个数和总和，最后得出平均值；
方法二：DFS：深度搜索，每次层数一样的加一起，记录个数，同理求平均值。

代码

BFS

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root)  {
        queue<TreeNode*> qu;
        vector<double> ans;
        if(root==nullptr)
            return ans;
        TreeNode* node=root;
        qu.push(root);

        while(!qu.empty())
        {
            int n=qu.size();
            long long sum=0;
            for(int i=0;i<n;i++)
            {
                node=qu.front();
                qu.pop();
                if(node->left)
                    qu.push(node->left);
                if(node->right)
                    qu.push(node->right);
                sum+=node->val;
            }
            ans.push_back((sum+0.0)/n);
        }
        return ans;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        vector<int> counts;
        vector<double> sums;

        dfs(root, 0, counts, sums);

        vector<double> ans;
        int size = sums.size();
        for (int i = 0; i < size; i++) {
            ans.push_back(sums[i] / counts[i]);
        }
        return ans;
    }

    void dfs(TreeNode* root, int level, vector<int> &counts, vector<double> &sums) {
        if (root == nullptr) {
            return;
        }
        if (level < sums.size()) {
            sums[level] += root->val;
            counts[level] += 1;
        } else {
            sums.push_back(1.0 * root->val);
            counts.push_back(1);
        }
        dfs(root->left, level + 1, counts, sums);
        dfs(root->right, level + 1, counts, sums);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

收获

巩固了树遍历的俩种常用且重要的方式DFS和BFS。