-
cache存储器最全详细介绍
Cache基本概念和原理
cache功能
cache是一种高速缓冲存储器,是为了解决CPU和主存之间速度不匹配而采用的一项重要技术

cache原理
cache原理是基于程序运行中具有的空间局限性和时间局限性特征。
程序A代码

地址存储情况
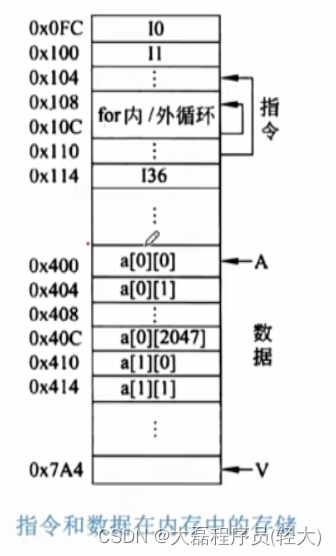
空间局限性:在最近的未来要用到的信息(指令和数据),很有可能与现在正在使用的信息在存储空间上是邻近的,如:数组元素、顺序执行的指令代码
时间局限性:在最近的未来要用到的信息,很可能是现在正在使用的信息, 如:循环结构的指令代码
基于局部性原理,不难想到,可以把CPU目前访问的地址“周围”的部分数据放在Cache中
性能分析

设tc为访问一次Cache所需时间,tm为访问一次主存所需时间
命中率H:CPU欲访问的信息已在Cache中的比率
缺失(未命中)率M=1-H
Cache——主存系统的平均访问时间t为:
情况1:先访问Cache,若Cache未命中再访问主存
t=Htc+(1-H)(tc+tm)
情况2:同时访问Cache和主存,若Cache命中则立即停止访问主存
t=Htc+(1-H)tm
练习题:

有待解决的问题
基于局部性原理,不难想到,可以把CPU目前访问的地址“周围”的部分数据放到Cache中。如何界定“周围”
将主存的存储空间“分块”,如:每1KB为一块。主存与Cache之间以“块”为单位进行数据交换

注:操作系统中,通常将主存中的“一个块”也称为“一个页/页面/页框”
Cache中的“块‘也称为”行“
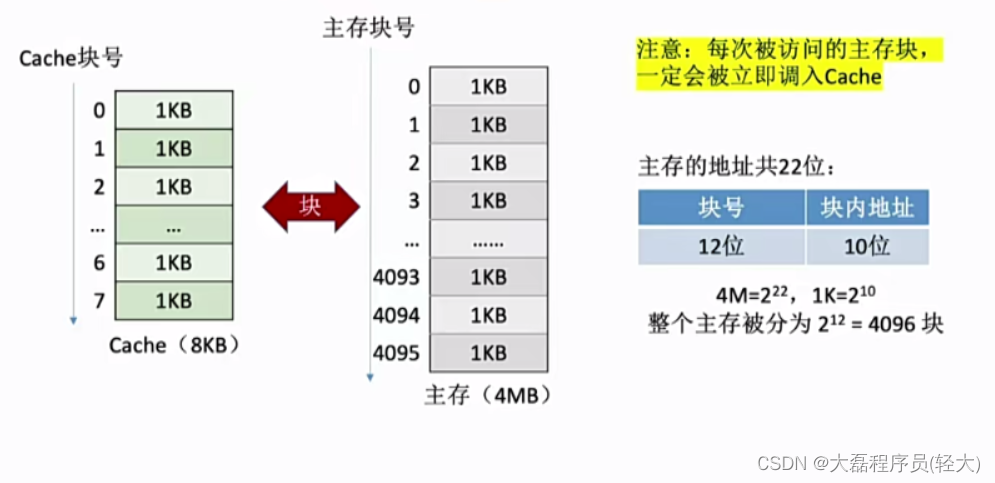
每次被访问的主存块,一定会被立即调入Cache
Cache和主存的映射关系
解决如何区分Cache与主存的数据块对应关系
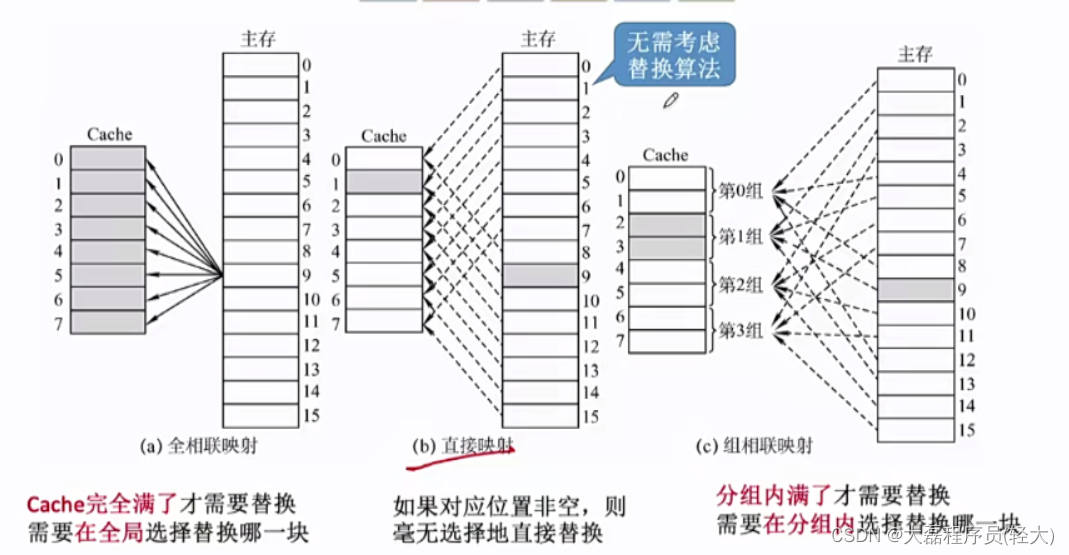
全相联映射(随意放)
主存可以放在Cache的任意位置
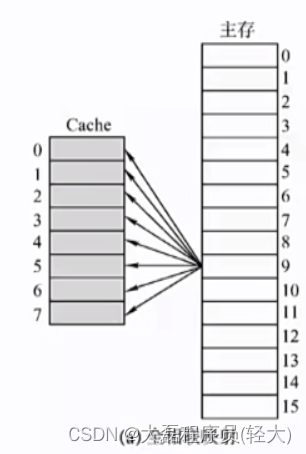
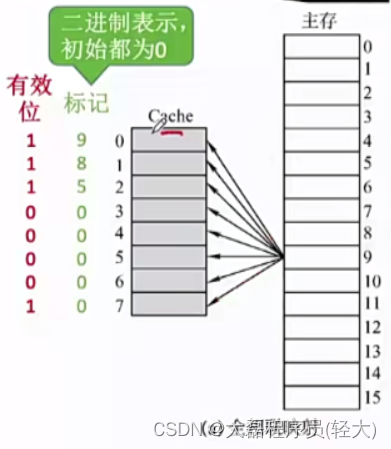
为了区分Cache中存放的是哪个主存块,需要给每个Cache块增加一个“标记”,记录对应的主存块号,还需要增加“有效位”来标记是否有效
如下图:0号Cache块存储的是9号主存,3号Cache块存储的不是0号主存(因为有效位是0)
举例说明如何映射:
假设某个计算机的主存地址空间大小为256MB,按字节编址,其数据Cache有8个Cache行(即Cache块,需要与主存块的大小相等),行长为64MB
因为主存地址空间大小为256MB,所以为2的28次方,因为Cache块与主存块的大小需要相等,所以主存块分为22块(2的28次方除于2的6次方)主存块号为22位,因为主存地址为28位,所以剩余6位给块内地址

因此每个主存块的地址范围如下:

因为随意放,可以将块号为0的副本到Cache的3号,块号为2的22次方-3的副本到Cache的1号,映射关系如下

CPU如何访存:
CPU访问主存地址1....1101001110:
第一步:主存地址前22位对比Cachezh9ong所有块的标记;
第二步:若标记匹配且有效位=1,则Cache命中,访问块内地址为001110的单元
第三步:若未命中或有效位=0,则正常访问主存
优点:Cache存储空间利用充分,命中率高;
缺点:查找“标记”最慢,有可能对比所有行的标记
直接映射(只能放特定位置)
每个主存块只能放到一个特定的位置:Cache块号=主存块号%Cache总块数
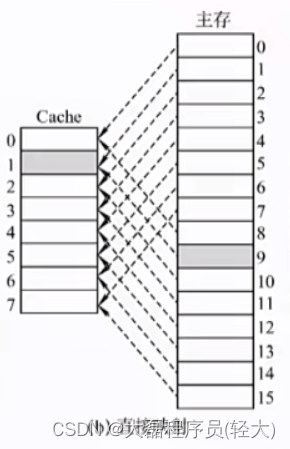
举例说明如何映射:
假设某个计算机的主存地址空间大小为256MB,按字节编址,其数据Cache有8个Cache行(即Cache块,需要与主存块的大小相等),行长为64MB
因为主存地址空间大小为256MB,所以为2的28次方,因为Cache块与主存块的大小需要相等,所以主存块分为22块(2的28次方除于2的6次方)主存块号为22位,因为主存地址为28位,所以剩余6位给块内地址

因此每个主存块的地址范围如下:

直接映射,主存块在Cache中的位置=主存块号%Cache总块数

Cache块中原本存储的是主存块号0,如果主存块号8想要存储在Cache中,由于8%8=0,所以需要将原来的Cache块中的0号进行覆盖,并将标记为修改为主存块8号的块号,如下图:

能否优化标记?
主存块号%Cache总块数(2的3次方)相当于留下最后三位二进制数
所以若Cache总块数=2的n次方,则主存块号末尾n位直接反应它在Cache中的位置,将主存块号的其余位作为标记即可
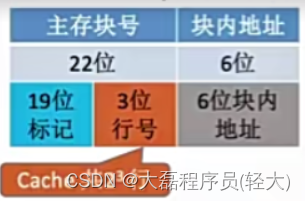
所以原本的22位主存块号被分为了两部分(19位的标记,3位的行号)

CPU如何访存:
CPU访问主存地址0...01000001110:
第一步:根据主存块号的后3位确定Cache行;
第二步:若主存块号的前19位与Cache标记匹配且有效位1,则Cache命中,访问块内地址为001110的单元
第三步:若未命中或有效位=0,则正常访问主存
优点:对于任意一个地址,只需对比一个“标记”,速度最快;
缺点:Cache存储空间利用不充分,命中率低
组相联映射(可放到特定分组)
Cache块分为若干组,每个主存块可放到特定分组中的任意一个位置:组号=主存块号%分组数

举例说明如何映射:
假设某个计算机的主存地址空间大小为256MB,按字节编址,其数据Cache有8个Cache行(即Cache块,需要与主存块的大小相等),行长为64MB,本例子采用2路组相联映射--2块为一组,分四组
因为主存地址空间大小为256MB,所以为2的28次方,因为Cache块与主存块的大小需要相等,所以主存块分为22块(2的28次方除于2的6次方)主存块号为22位,因为主存地址为28位,所以剩余6位给块内地址

组相联映射,所属分组=主存块号%分组数
和直接映射类似,由于分为四组为2的2次方,主存块号%2的2次方,相当于留下最后两位,所以所属同一组,主存块号的后两位必定会一样,所以将主存块号分为以下
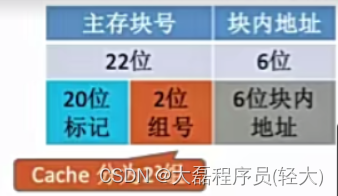

CPU如何访存:
CPU访问主存地址1..1101001110:
第一步:根据主存块号的后2位确定所属分组;
第二步:若主存块号的前20位与分组内的某个标记匹配且有效位1,则Cache命中,访问块内地址为001110的单元
第三步:若未命中或有效位=0,则正常访问主存
优点:另外两种方式的折中,综合效果最好
Cache与主存映射方式下主存地址格式
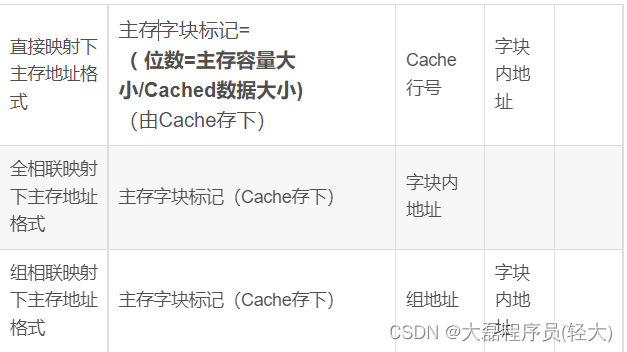
Cache替换算法
Cache替换算法用来解决Cache很小,主存很大。如果Cache满了怎么办的问题
替换算法解决的问题
随机算法(RAND)
随机算法(RAND,Random)- -若Cache已满,则随机选择一块替换。
设总共有4个Cache块,初始整个Cache为空。采用全相联映射,依次访问主存块{1,2,3,4,1,2,5,1,2,3,4,5},过程如下:

随机算法 - -实现简单,但没有完全考虑局部性原理,命中率低,实际效果很不稳定
先进先出算法(FIFO)
先进先出算法(FIFO,First In First Out) - - 若Cache已满,则替换最先被调入Cache的块
设总共有4个Cache块,初始整个Cache为空。采用全相联映射,依次访问主存块{1,2,3,4,1,2,5,1,2,3,4,5},过程如下:
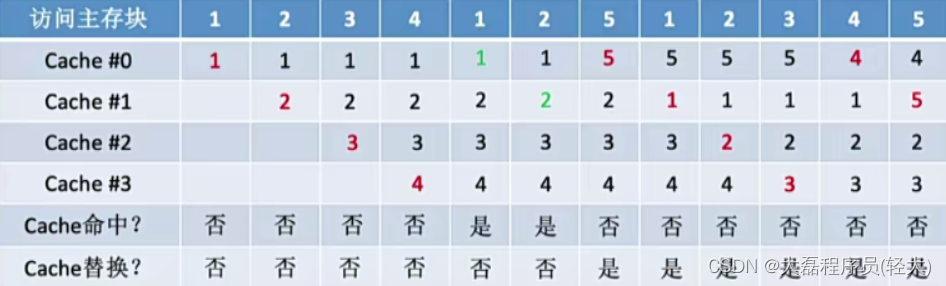
抖动现象:频繁的换入换出现象(刚被替换的块很快又被调入)
先进先出算法 - - 实现简单,最开始按#0#1#2#3放入Cache,之后轮流替换#0#1#2#3
FIFO依然没考虑局部性原理,最先调入Cache的块也有可能是被频繁访问的
近期最少使用算法(LRU)
近期最少使用算法(LRU,LeastRecently Used) - - 为每一个Cache块设置一个“计数器”,用于记录每个Cache块已经很久没有被访问了。
当Cache满后替换“计算器”最大的设总共有4个Cache块,初始整个Cache为空。采用全相联映射,依次访问主存块{1,2,3,4,1,2,5,1,2,3,4,5},过程如下:

考试的时候:比如访问5号主存块,以5号为起点,往左边看,最后一个Cache号即为需要被替换的
LRU算法 - - 基于“局部性原理”,近期被访问过的主存块,在不久的将来也很有可能被再次访问,因此淘汰最久没被访问过的块是合理的。LRU算法的实际运行效果优秀,Cache命中率高。
但若被频繁访问的主存块数量>Cache行的数量,则有可能发生“抖动”,如:{1,2,3,4,5,1,2,3,4,5,1,2....} 5>4
最不经常算法(LFU)
最不经常算法(LFU,Least Frequently Used) - - 为每一个Cache块设置一个“计数器”,用来记录每个Cache块被访问过几次。当Cache满后替换“计数器”最小的
设总共有4个Cache块,初始整个Cache为空。采用全相联映射,依次访问主存块{1,2,3,4,1,2,5,1,2,3,4,5},过程如下:
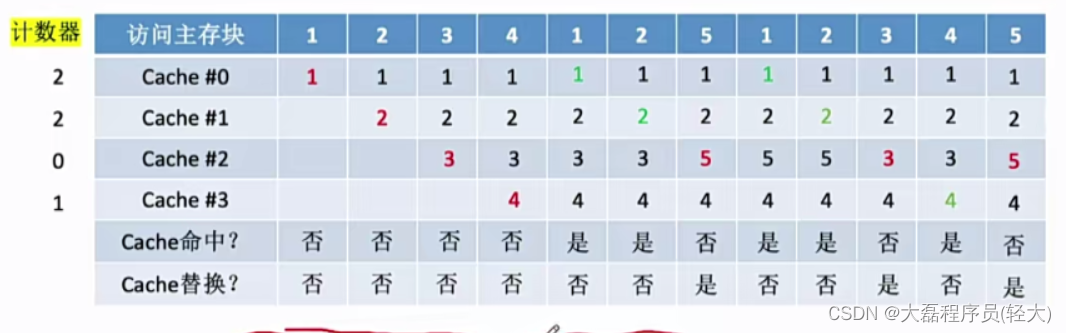
计数器的值可能很大
LFU算法--曾将被访问的主存块在未来不一定会用到(如:微信视频聊天相关的块),并没有很好地遵循局部性原理,因此实际运行效果不如LRU
Cache写策略
解决CPU修改了Cache中的数据副本,如何确保主存中数据母本的一致性
写命中
写回法
当CPU对Cache写命中时,只修改Cache的内容,而不是立即写入主存,只有当此块被换出时才写回主存

给Cache增加一个脏位,用来表示是否被修改过
虽然这种方法减少了访存次数,但存在数据不一致的隐患。
全写法
当CPU对Cache写命中时,必须把数据同时写入Cache和主存,一般使用写缓冲(write buffer)
写缓冲是SARM实现的FIFO队列
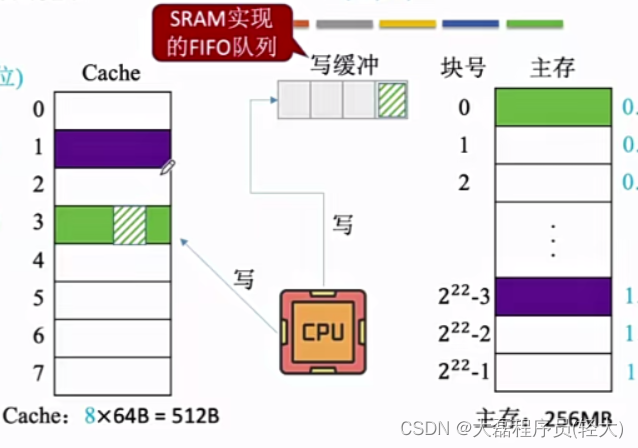
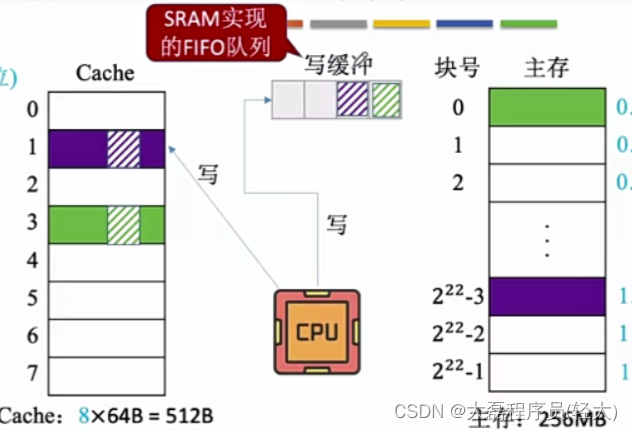
CPU将分别向Cache中和写缓冲中执行写操作,被修改数据写入缓冲中,CPU就可以去做其它事情了,此时在专门的控制电路控制下逐一向主存中写回

使用写缓冲,CPU写的速度很快,若写操作不频繁,则效果很好,但是若操作很频繁,可能会因为写缓冲饱和而发生阻塞
写不命中
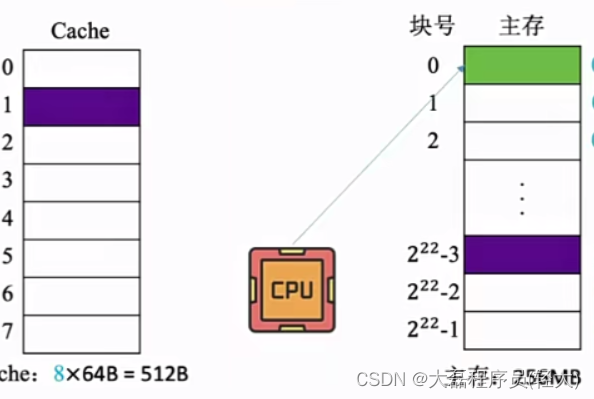
写分配法
当CPU对Cache写不命中时,把主存中的块调入Cache,在Cache中修改。通过搭配写回法使用
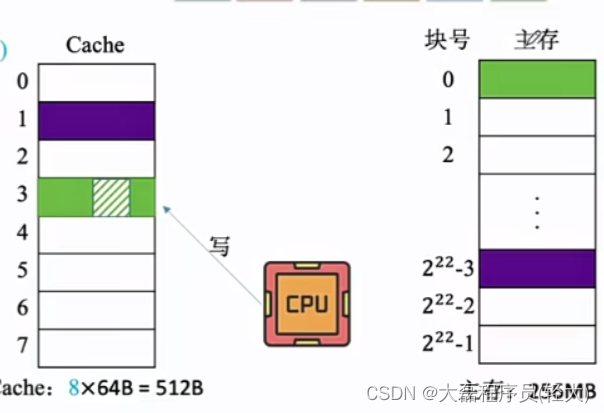
非写分配法
当CPU对Cache写不命中时只写入主存,不调入Cache。搭配全写法使用

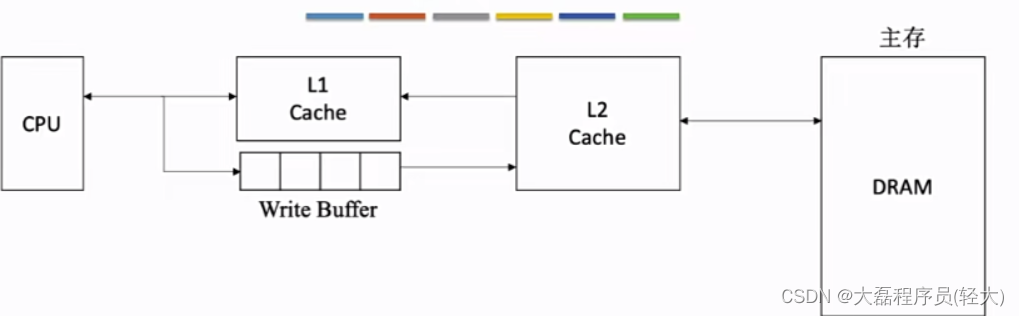
多级Cache
现代计算机常采用多级Cache
离CPU越近的速度越快,容量越小,离CPU越远的速度越慢,容量越大
越接近CPU的Cache存储的是前一个Cache中的一小部分内容
各级Cache之间常采用“全写法+非写分配法”
Cache-主存之间常采用“写回法+写分配法”
-
相关阅读:
2022牛客暑期多校训练营9(总结+补题)
Helm3模板-其他注意事项
每天都很煎熬,领导派的活太难,真的想跑路了
Stream流总结
Redux Toolkit
Redis 底层的数据结构
Vue源码:手写patch函数,diff算法
LNMP架构:搭建Discuz论坛
[JavaWeb]——JWT令牌技术,如何从获取JWT令牌
基于JavaSwing开发进销存管理系统的设计与实现 课程设计 大作业 毕业设计
- 原文地址:https://blog.csdn.net/m0_59860403/article/details/127695569