-
二次型和矩阵正定的意义
一、概述
1、矩阵正定的意义
通过矩阵来研究二次函数(方程),这就是线性代数中二次型的重点。2、通过矩阵来研究二次方程因为二次函数(方程)的二次部分最重要,为了方便研究,我们把含有n个变量的二次齐次函数:
f ( x 1 , x 2 , ⋅ , x n ) f(x1,x2,⋅,xn) f(x1,x2,⋅,xn)
= a 11 x 12 + a 22 x 22 + ⋯ + a n n x n 2 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + ⋯ + 2 a n − 1 , n x n − 1 x n f ( x 1 , x 2 , ⋅ , x n ) =a11x12+a22x22+⋯+annxn2+2a12x1x2+2a13x1x3+⋯+2an−1,nxn−1xnf(x_1,x_2,\cdot ,x_ n) =a11x12+a22x22+⋯+annxn2+2a12x1x2+2a13x1x3+⋯+2an−1,nxn−1xnf(x1,x2,⋅,xn)
= a 11 x 1 2 + a 22 x 2 2 + ⋯ + a n n x n 2 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + ⋯ + 2 a n − 1 , n x n − 1 x n f ( x 1 , x 2 , ⋅ , x n ) =a_{11}x_1^2+a_{22}x_2^2+\cdots +a_{nn}x_ n^2+2a_{12}x_1x_2+2a_{13}x_1x_3+\cdots +2a_{n-1,n}x_{n-1}x_ nf(x_1,x_2,\cdot ,x_ n) =a11x12+a22x22+⋯+annxn2+2a12x1x2+2a13x1x3+⋯+2an−1,nxn−1xnf(x1,x2,⋅,xn)
= a 11 x 1 2 + a 22 x 2 2 + ⋯ + a n n x n 2 + 2 a 12 x 1 x 2 + 2 a 13 x 1 x 3 + ⋯ + 2 a n − 1 , n x n − 1 x n =a_{11}x_1^2+a_{22}x_2^2+\cdots +a_{nn}x_ n^2+2a_{12}x_1x_2+2a_{13}x_1x_3+\cdots +2a_{n-1,n}x_{n-1}x_ n =a11x12+a22x22+⋯+annxn2+2a12x1x2+2a13x1x3+⋯+2an−1,nxn−1xn
称为二次型。实际上我们可以通过矩阵来表示二次型:
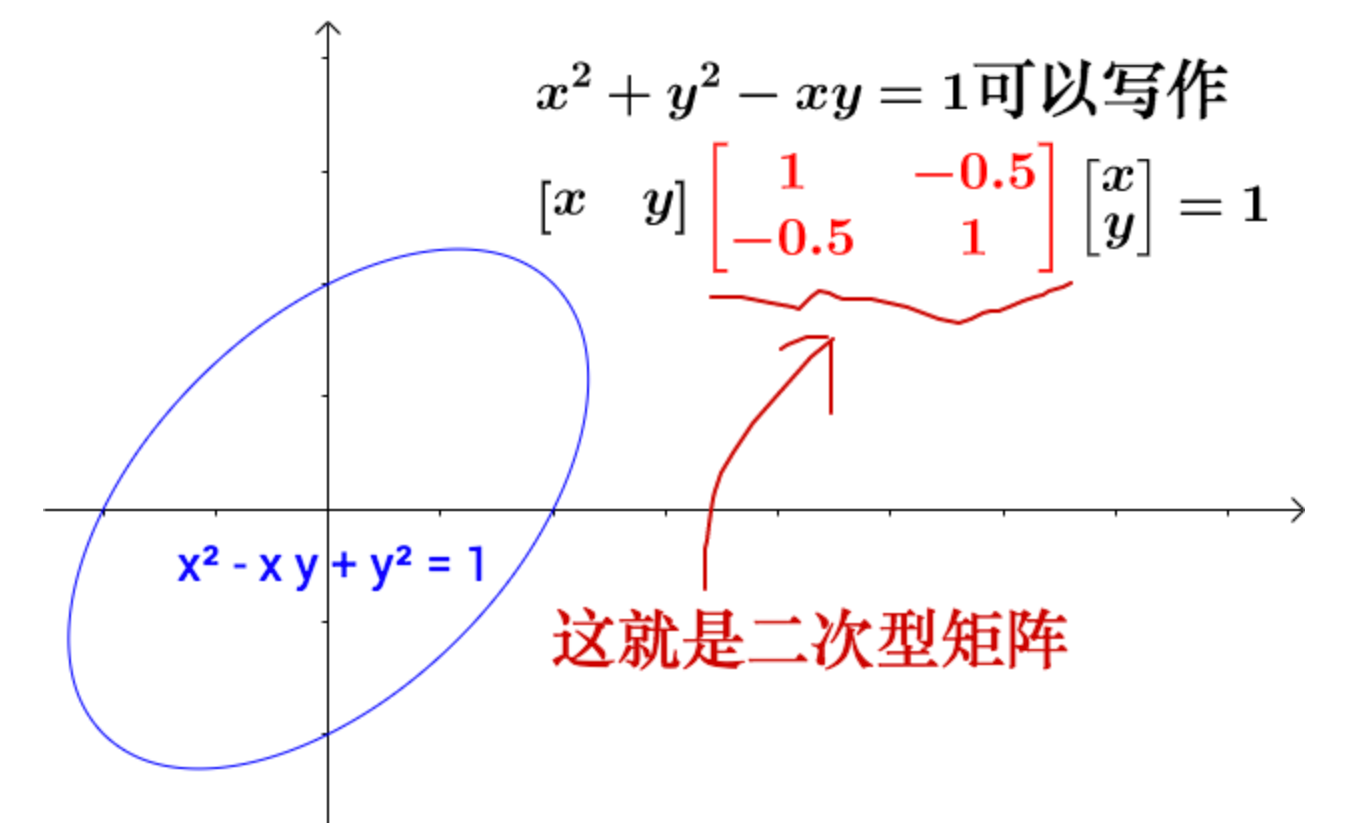
更一般的:
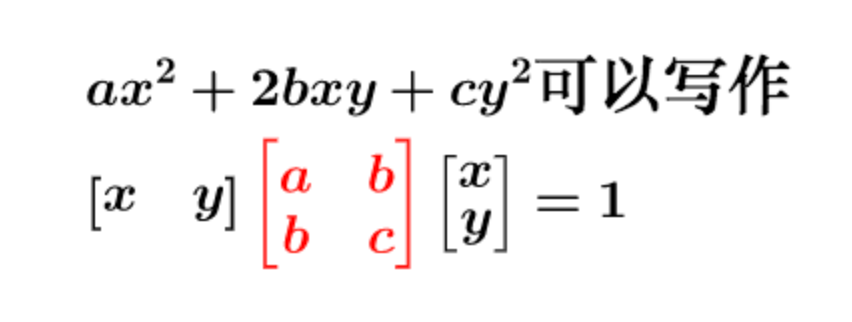
可以写成更线代的形式:
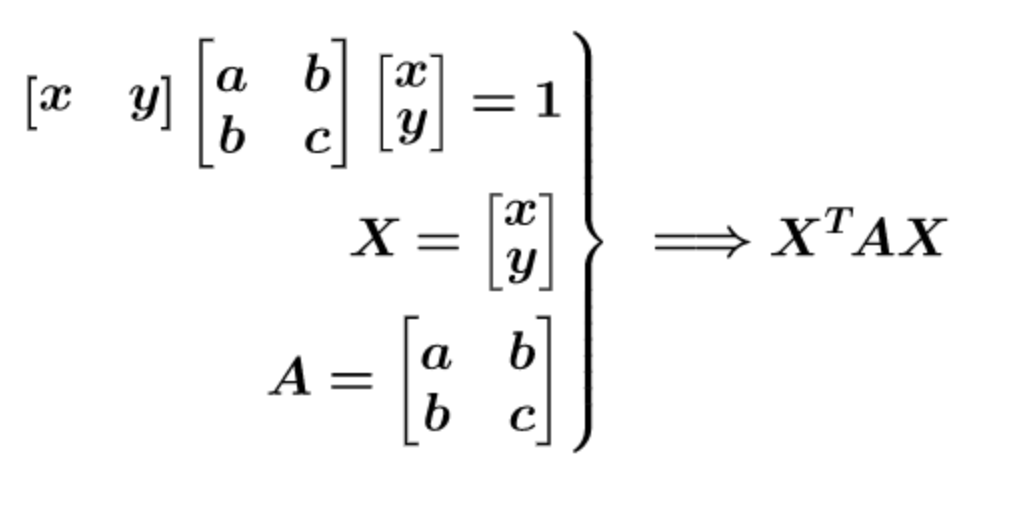 所以有下面一一对应的关系:
所以有下面一一对应的关系:

在线代里面,就是通过一个对称矩阵,去研究某个二次型。3、正定正定是对二次函数有效的一个定义,对方程无效。对于二次型函数, f ( x ) = x T A x : f(x)=x^{T}Ax: f(x)=xTAx:

正定图示
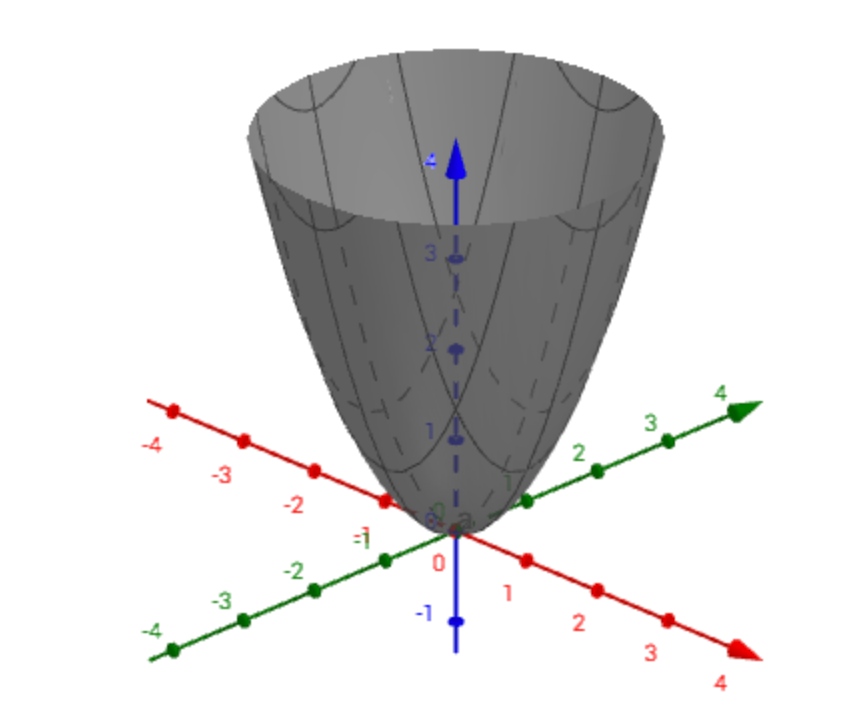
半正定图示
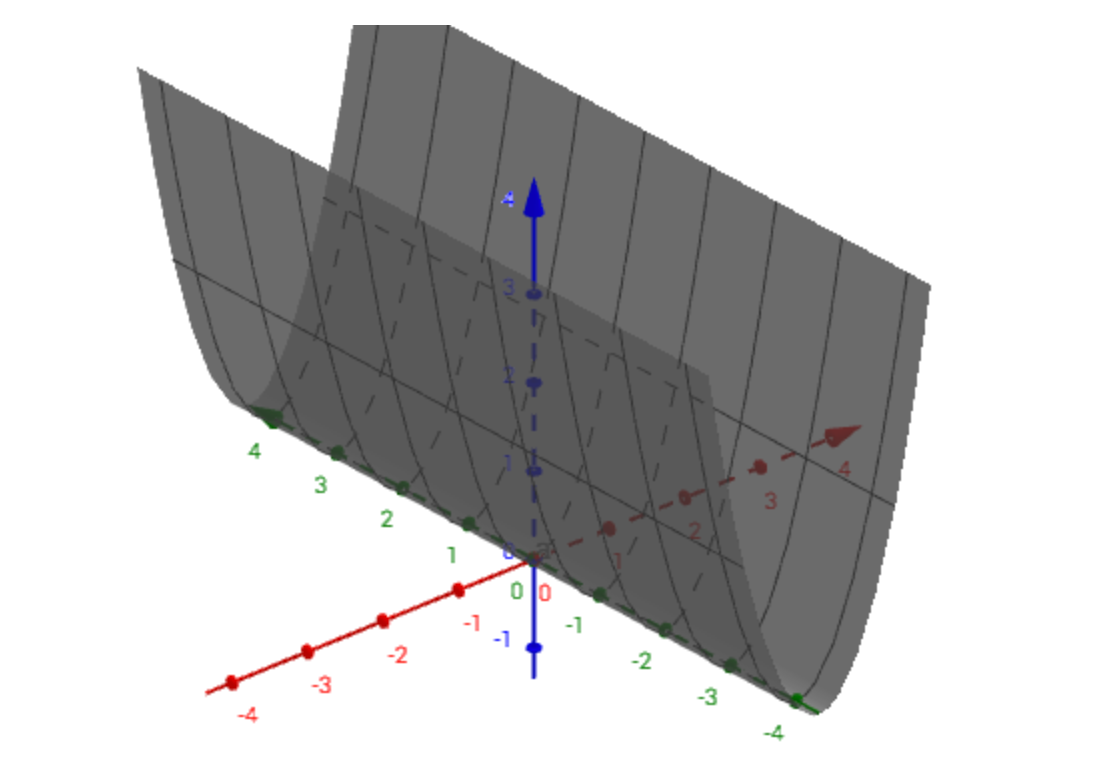
不定图示
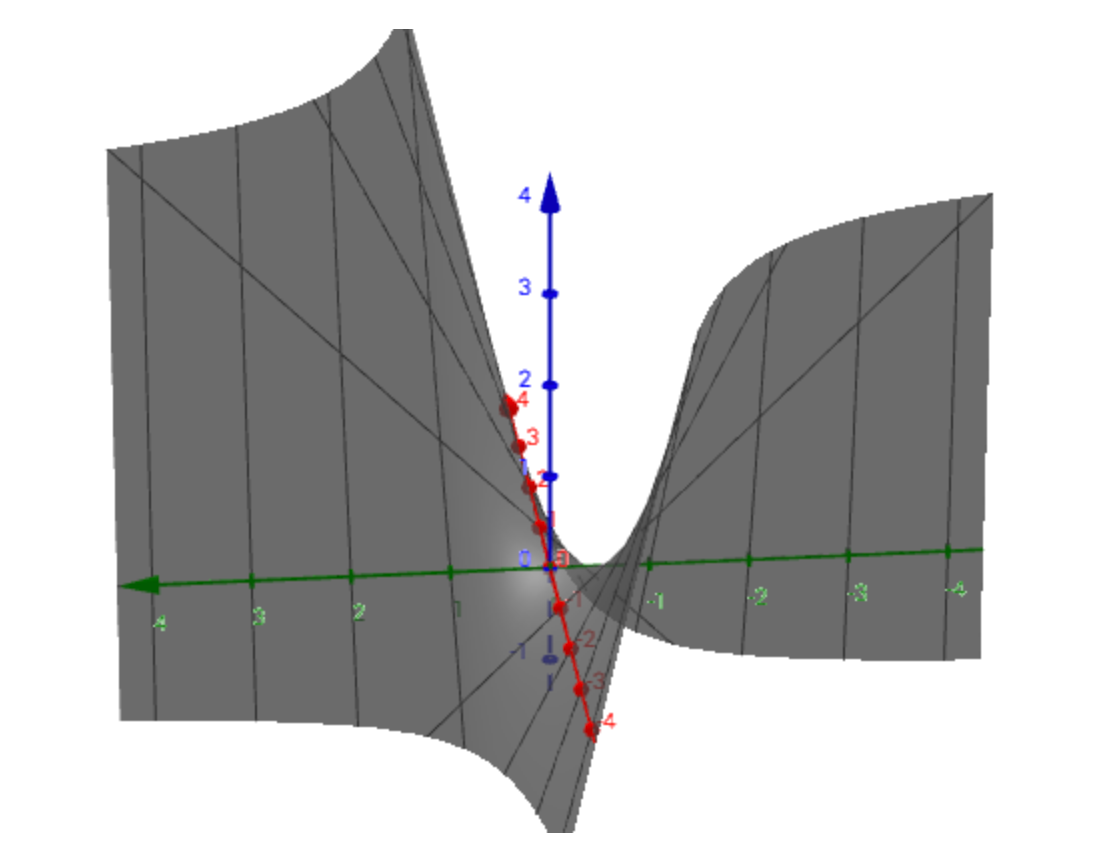
二、其他角度
- 数学视角看,当我们说矩阵正定,相当于对矩阵做了相当强的一种限制,那么在这个限制里就会发现相当多有趣的性质,另外有许多矩阵是正定的,比如协方差矩阵,动力矩阵等等。这就给了数学家研究归纳性质的强烈兴趣。
- 从系统角度看,如果一个矩阵是正定的,那么我们可以简单理解这个系统拥有全局最大值。而绝大部分问题都可以抽象为解决一个优化问题,如果能证明或者将问题用正定矩阵表示,那么从理论上该问题便拥有全局最优解。比如如果矩阵二阶导为正定矩阵
x
T
A
x
>
0
x^TAx>0
xTAx>0,则证明其具有局部最大值解,反之
x
T
A
x
>
0
x^TAx>0
xTAx>0 则证明其具有局部最小值解,如果不满足上述两种则证明函数会有鞍点(saddle point)。从下图可以看 A 为最小值,B为鞍点,C为最大值。而如果理论上拥有全局最优解,便会给我们使用很多已知成熟的方式去求解最优值的方法,(简单举个例子:比如使用Hessian矩阵求解最优等),这也是机器学习,优化问题最喜欢去研究和解决的情况。
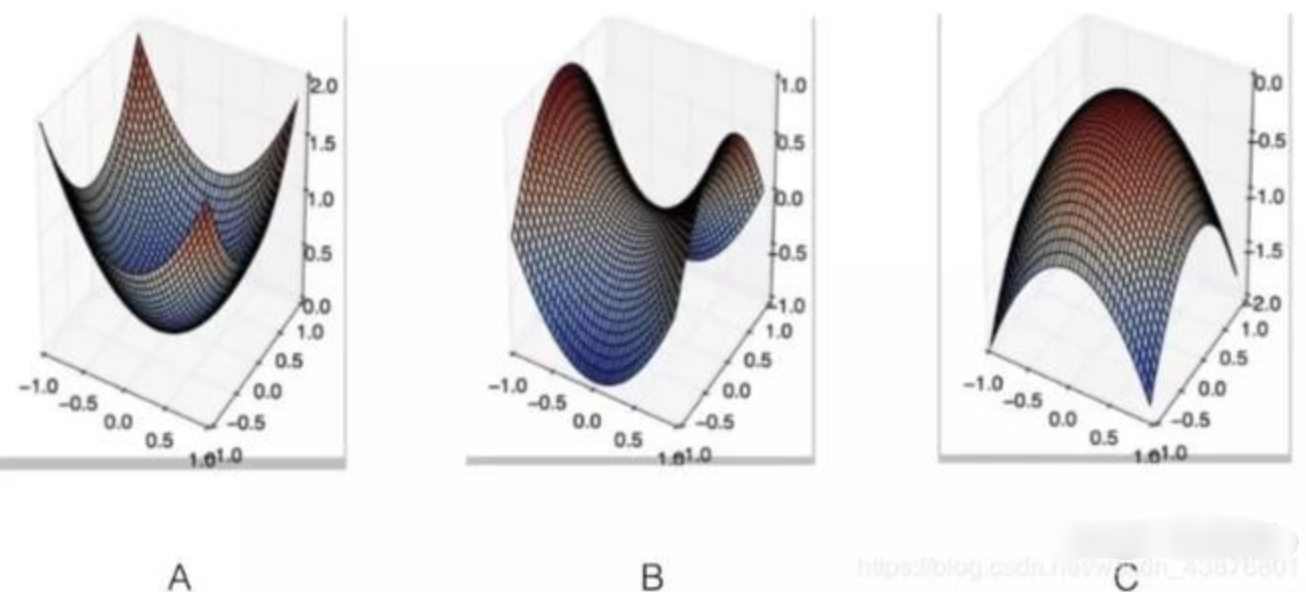
- 可以将正定矩阵理解为矩阵版标量正系数。进一步讲 比如 在标量中: y = ax 当a > 0 时 y 将与x的正负号相同,即如果x > 0 则 y > 0, x < 0 则y <0。与a 相乘不会改变正负号。那该性质如何在多维空间中表示呢?这里我们说,简单理解正定矩阵便是符合标量中a性质的矩阵。也则是 x T A x > 0 x^TAx>0 xTAx>0的含义。A正定,则其中一个性质是A与X同向夹角小于九十度,所以AX将会与X同向,而不会将X变换到与之完全相反的方向。总结:在标量空间中我们拥有y = ax, 我们可以规定a > 0。 而在多维空间中,Y = AX, 我们定义矩阵A > 0 的方式便是正定,而矩阵A > 0 不能这么定义, x T A x > 0 x^TAx>0 xTAx>0便是正确的定义方式,其在标量空间中等价于 a > 0。
Ref:
[1].二次型的意义是什么?有什么应用?
[2].一个矩阵正定(Possitive definite) 到底能说明什么,能解决什么问题? -
相关阅读:
MySQL - DML数据增删改
不要小看一个Redis,从头到尾全是精华,阿里Redis速成笔记太香了
SpringBoot3使用Swagger
锐捷ISIS基础实验
砥砺的前行|基于labview的机器视觉图像处理|NI Vision Assisant(六)——Binary(二值图) 功能
打印机选择问题咨询 -11111
NEFU离散数学实验1-排列组合
洛谷P1202 黑色星期五Friday the Thirteenth
tcp/ip 协议解析和开发项目传输数据的常见服务
【Opencv450】HOG+SVM 与Hog+cascade进行行人检测
- 原文地址:https://blog.csdn.net/qq_22866291/article/details/127266480