【754. 到达终点数字】

来源：力扣（LeetCode）

描述：

在一根无限长的数轴上，你站在0的位置。终点在target的位置。

你可以做一些数量的移动 numMoves :

• 每次你可以选择向左或向右移动。

• 第 i 次移动（从 i == 1 开始，到 i == numMoves ），在选择的方向上走 i 步。

给定整数 target ，返回 到达目标所需的 最小 移动次数(即最小 numMoves ) 。

示例 1:

输入: target = 2
输出: 3
解释:
第一次移动，从 0 到 1 。
第二次移动，从 1 到 -1 。
第三次移动，从 -1 到 2 。
1
2
3
4
5
6

示例 2:

输入: target = 3
输出: 2
解释:
第一次移动，从 0 到 1 。
第二次移动，从 1 到 3 。
1
2
3
4
5

提示:

• -10⁹ <= target <= 10⁹
• target != 0

方法：分析 + 数学

思路

  假设移动了 k 次，每次任意地向左或向右移动，那么最终达到的位置实际上就是将 1, 2, 3, …, k 这 k 个整数添加正号或负号后求和的值。如果 target < 0，可以将这 k 个数的符号全部取反，这样求和的值为 −target > 0。因此我们可以只考虑 targe t> 0 的情况。

  设 k 为最小的满足

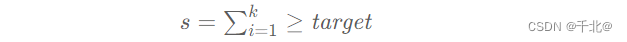
的正整数。如果 s = targets，那么答案即为 k。如果 s > targets，需要在部分整数前添加负号来将和凑到 target。

如果 delta = s − target 为偶数，则目标为从 1 到 k 中找出若干个整数使得他们的和为 delta / 2，下面证明一定能到找这样的若干个整数。

• 如果 k ≥ delta / 2，那么只需要选出一个 delta / 2。

• 否则，可以先选出 k，再从剩余的 11 到 k−1 中选出和为 delta / 2 − k 的若干个数即可，这样就把原问题变成了一个规模更小的问题。因为 delta / 2 < s，因此一定可以找出若干个数使得和为 delta / 2。

如果 delta 为奇数，那么就无法凑出这样的若干个数字。考虑 k+1 和 k+2，

中必有一个和 s 的奇偶性相同，使得此时的 delta 为偶数。此时也满足 ⌊ delta / 2⌋ < ∑，因此也可以找到若干个数的和为 ⌊delta / 2⌋。

代码：

class Solution {
public:
    int reachNumber(int target) {
        target = abs(target);
        int k = 0;
        while (target > 0) {
            k++;
            target -= k;
        }
        return target % 2 == 0 ? k : k + 1 + k % 2;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

复杂度分析
时间复杂度：O(target)。循环内最多执行 O(target)次。
空间复杂度：O(1)。只使用常数空间。
author：力扣官方题解