并查集_find()_连通块_食物链

并查集

1.解决问题

• 将两个集合合并

• 询问两个元素是否在一个集合当中

注：每个集合用树的形式维护（根节点编号记为树的编号）

2.所需数组

p[] 存当前节点的父亲

3.问题

• 如何判断树根？ if(p[x] == x)

• 如何求x集合编号（即如何求根节点）？ while(p[x] != x) x=p[x];

  • 优化：路径压缩，搜索一遍，就把路径上所有点直接连根节点

• 如何合并两个集合？ p[x] = y;（连根）

如上维护了 可判断两个数是否在同一个集合 以及 合并集合

4.关键函数

返回x所在集合编号（返回x的祖宗节点） + 路径压缩（在find函数回溯时，会把每个节点的父节点设置为根节点）

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}
1
2
3
4
5

5.拓展1 - 连通块

① 问题分析

用集合来维护连通块

• 初始时每个点各自为一个集合

• Q2中需判断连通块中的数量，因此除去基本的（可判断两个数是否在同一个集合 以及 合并集合）维护，还需要维护 连通块的大小

• cnt[] 存储集合的大小（连通块中点的数量），只保证根节点cnt有意义即可

② 具体代码

#include 

using namespace std;

const int N = 100010;

int p[N], cnt[N];

//返回根节点值 + 路径压缩（函数回溯时，从上至下p[x]更新为根节点值）
int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    int n,m;
    scanf("%d%d",&n, &m);

    //初始化 - 每个数自己是一个集合，且大小为1；每个数大小为1
    for(int i = 1; i <= n; i++) 
    {
        p[i] = i;
        cnt[i] = 1;
    }

    while(m--)
    {
        char op[3];
        int a, b;
        scanf("%s",op);
        if(op[0] == 'C')
        {
            scanf("%d%d",&a,&b);
            if(find(a) != find(b)) 
            {
                // 以下两个顺序不可颠倒：先将b所在集合的大小增为两者之和，再将a的根节点的父亲设为b（若颠倒顺序，两个集合已经合并，更新cnt后b所在集合大小为两个集合之和的二倍）
                cnt[find(b)] += cnt[find(a)];
                p[find(a)] = find(b);    //将a所在集合并入b所在集合中 - a的根节点的父亲改为b的根节点
            }
            else continue;
        }else if(op[1] == '1')
        {
            scanf("%d%d", &a,&b);
            if(find(a) == find(b)) cout << "Yes" << endl;
            else cout << "No" << endl;
        }else
        {
            scanf("%d", &a);
            printf("%d\n",cnt[find(a)]);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

6.拓展2 - 食物链

① 问题分析

• 题意：从A吃B、B吃C、C吃A构成环形来看，只要知道三类动物中的两种关系即可推断出第三种关系。

• 将每个动物不论同类/异类都放入同一个集合，使用并查集的方法解决该问题。

• 如图所示：将各动物连成树，设此处b吃a、c吃b，则a吃c。

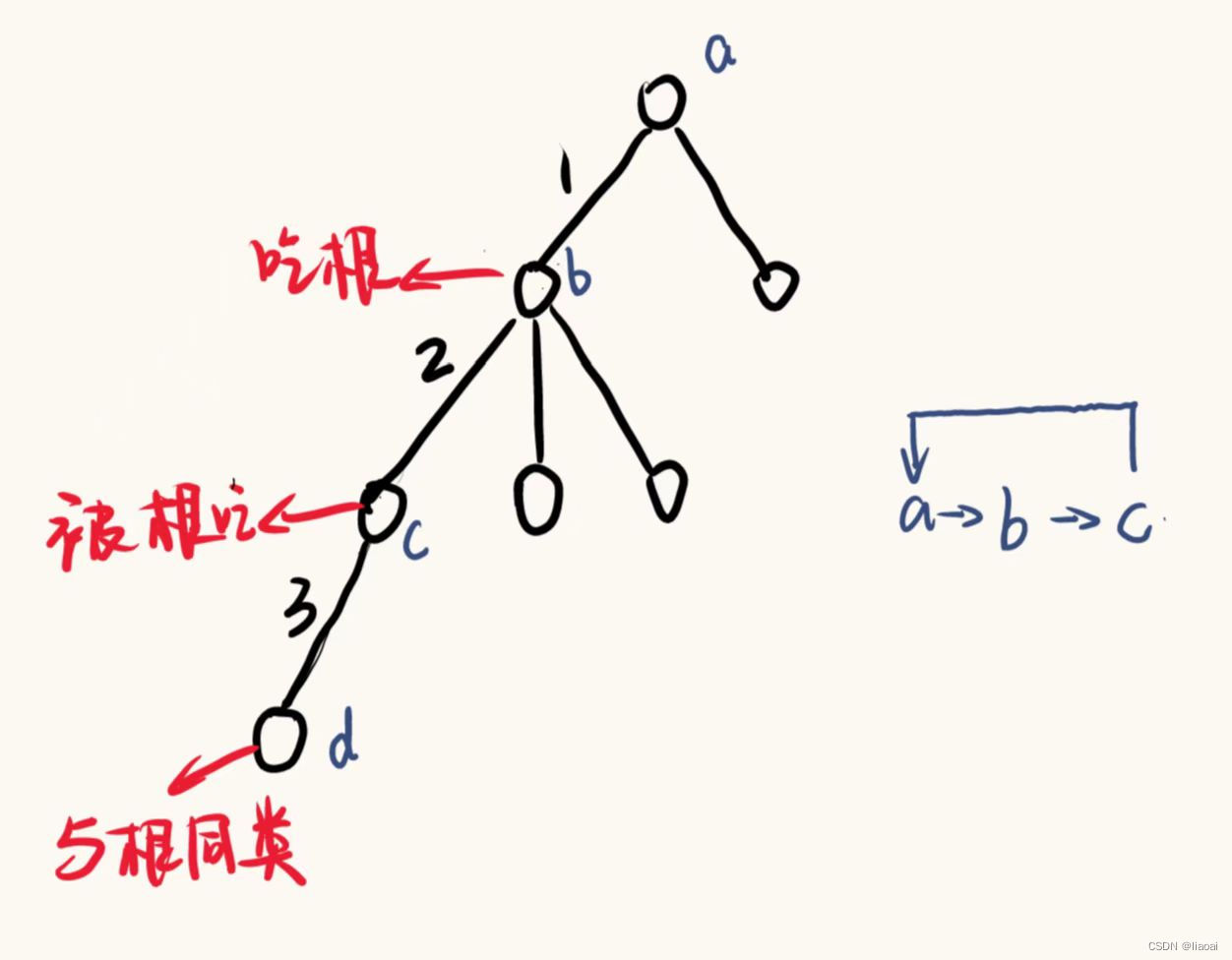
以上可推断出，每三个动物一个循环，第四个动物即为根同类。

• 并查集基础方法中能够实现：返回根节点 + 路径压缩，此处可以再维护节点与根节点的距离，此处的距离并不是我们认为的简单的距离，可以看作是一代、两代…

• 以上可以推出：距离 mod 3 => 余1：可吃根；余2：可被根吃；余0：与根同类

② find()函数

p[]：存入节点的父节点

d[]：存入节点到父节点的距离

在路径压缩的过程中，可以将x到根节点的距离设为其路径上所有点的距离之和。

int find(int x)
{
    if(p[x] != x)
    {
        int t = find(p[x]);   //先压缩了p[x]
        d[x] += d[p[x]];    //d[x]更新为其到根节点的距离
        p[x] = t;
    }
    return p[x];
}
1
2
3
4
5
6
7
8
9
10

③ 具体代码

对于假话的判断如下：

• x/y大于n

• x/y符合条件时：px => x的根节点 py => y的根节点

  t==1（输入两节点同类）时

  • 两节点在同一集合中（之前输入中有过它俩之间的关系）：x和y同类 <==> 若d[x]和d[y]分别 mod 3的结果相同即为真话。

  • 两节点不在同一集合中：将两个节点所在集合合并，假设x所在集合并入y所在集合，需要定义d[px]的值(d[x] + ? - d[y]) % 3 == 0

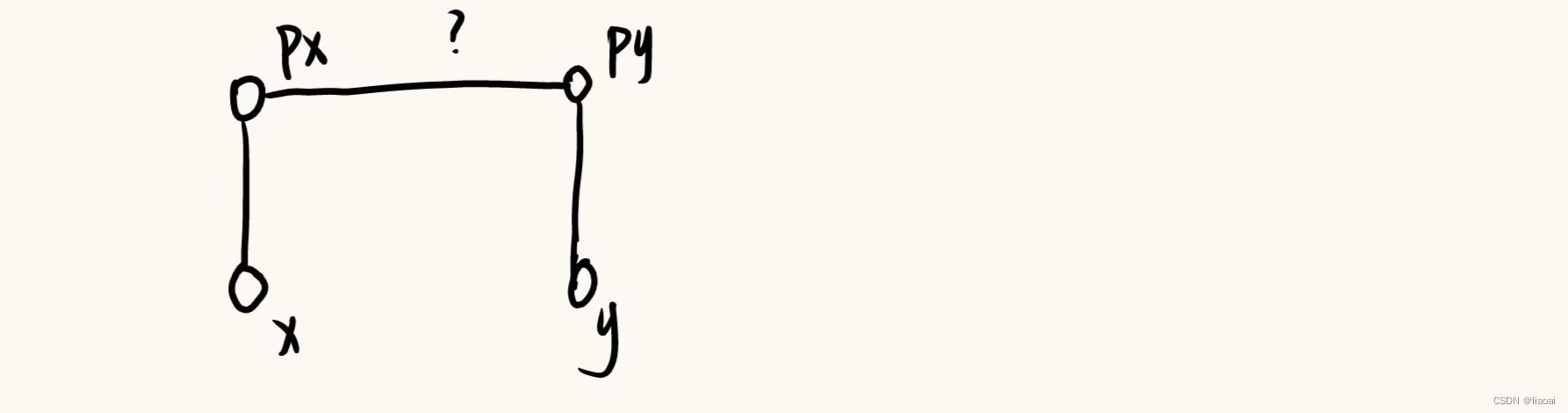
t==2（x吃y）时

• x == y 同类吃同类，为假话
• 两节点在同一集合中（之前输入中有过它俩之间的关系）：x吃y <==> (d[x]-1) mod 3 与 d[y] mod 3 相等
• 两节点不在同一集合中：将两个节点所在集合合并，假设x所在集合并入y所在集合，需要定义d[px]的值。(d[x] + ? - 1- d[y]) % 3 == 0

#include 

using namespace std;

const int N = 100010;

//d[i] 存i到其父节点的距离
int p[N],d[N];

//返回根节点 + 路径压缩 + d[x]更新为其到根节点的距离
int find(int x)
{
    if(p[x] != x)
    {
        int t = find(p[x]);
        d[x] += d[p[x]];    //d[x]更新为其到根节点的距离
        p[x] = t;
    }
    return p[x];
}

int main()
{
    int res = 0;
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i = 1; i <= n; i++)
    {
        p[i] = i;   //d[]初始即为0，不必初始化
    }
    while(k--)
    {
        int t,x,y;
        scanf("%d%d%d",&t,&x,&y);
        if(x > n || y > n) res ++;
        else
        {
            int px = find(x), py = find(y);     //存入x、y的根节点
            if(t == 1)  //xy同类
            {
                if(px == py && (d[x]-d[y])%3) res ++;       //两者已在一个集合中
                else if(px != py)
                {
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            }
            else
            {
                if(x == y) res ++;
                else if(px == py && (d[x] - d[y] - 1)%3) res ++;
                else if(px != py)
                {
                    p[px] = py;
                    d[px] = d[y] + 1 -d[x];
                }
            }
        }
    }
    printf("%d",res);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62