代码随想录动态规划——回文字串（三种方法求解，dp/中心扩散1/中心扩散2）

题目

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：“abc” 输出：3 解释：三个回文子串: “a”, “b”, “c”

示例 2：

输入：“aaa” 输出：6 解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

提示：

输入的字符串长度不会超过 1000

思路

暴力法：两层for循环，遍历区间起始位置和终止位置，然后判断这个区间是不是回文

动规五部曲：

1. 确定dp数组和下标
   布尔类型的dp[i][j]表示区间范围[i，j]的区间是否是回文子串，其中j ≥ i

2. 确定递推公式
   仍然是两种情况：s[i]表示位置i的元素，s[j]表示位置j的元素
   （1）s[i] != s[j]，那么dp[i][j] = false
   （2）s[i] == s[j]，有三种情况
   ①下标 i 与 j 相同，表示的是同一个字符，如a，当然是回文子串
   ②下标 i 与 j 相差为1或者相差为2，例如aa，axa（x为任意字符）也都是回文子串
   即 j-i <= 1的时候，返回true
   ③下标：i 与 j 相差大于2的时候，例如cabac，此时s[i]与s[j]已经相同了都为c，这时看 i 到 j 区间是不是回文子串就只需要看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true

3. dp数组初始化：全部初始化为false，表示未匹配上的情况

4. 确定遍历顺序：
   从递推公式中可以看出，情况③是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的
   dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：
   
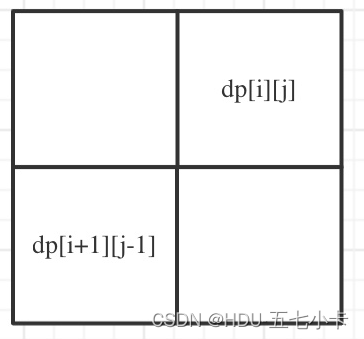
   所以是从下往上（i从大到小），从左往右的遍历顺序，为了保证dp[i + 1][j - 1]都是经过计算，但是遍历的时候外层for可以从 j 开始，内层for从i开始，这样就可以不用倒着遍历了

5. 举例推导dp数组：
   举例，输入：“aaa”，dp[i][j]状态如下：
   
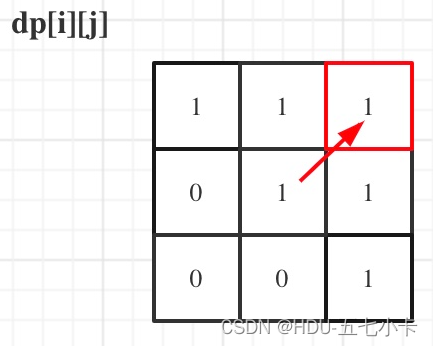
   java代码如下：

class Solution{
	public int countSubstrings(String s){
		int ans = 0;
		int len = s.length();
		if(s == null || s.length() == 0){
			return 0;
		}
		boolean[][] dp = new boolean[len][len];
		for(int j = 0; j < len; j++){
			for(int i = 0; i <= j; i++){
				//当两端字母一样时，才可以两端收缩进一步判断
				 if (s.charAt(i) == s.charAt(j)){
				 	if(j - i <= 2){
				 		dp[i][j] = true;
				 	} else {//当i,j相差大于2时
				 		dp[i][j] = dp[i+1][j-1];
				 	}
				 } else {//如果不相等
				 	dp[i][j] = false;
				 }
			}
		}
		//遍历每一个字串，统计回文串个数
		for(int i = 0 ; i < len; i++){
			for(int j = 0; j < len; j++){
				if(dp[i][j] == true)
					ans++;
			}
		}
		return ans;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

• 时间复杂度：O(n^2)
• 空间复杂度：O(n^2)

双指针法（中心扩散法）：比较推荐的方法

本题的动态规划空间复杂度较高，推荐考虑双指针法

确定回文串，就是找中心然后向两边扩散看是不是对称的就可以了，确定有多少个回文字串，中心扩散法，可以理解为，遍历每个中心点，判断每个中心点左右是不是回文串，是的话左–右++再继续判断

只不过在遍历中心的时候，中心点会有两种情况：
一个元素可以作为中心点，两个元素也可以作为中心点，给定一个字符串s，长度为len，则中心点的个数为2 * len - 1，分别是len个单字符和len-1个双字符，如 “abcde”，那么可能的中心点为“a”、“b”、“c”、“d”、“e”、“ab”、“bc”、“cd”、“de”一共2 * 5-1=9个

java代码如下：

class Solution{
	public int countSubstrings(String s){
		int ans = 0;
		int len = s.length();
		if(s == null || s.length() == 0){
			return 0;
		}
		for(int center = 0; center < 2 * len - 1; center++){//通过遍历每个回文中心，向两边扩散，并判断是否回文字串
			//left、right和中心点center的关系
			//首先是left，是一个很明显的2倍关系，其次是right，可能和left指向同一个（偶数时），也可能往后移动一个（奇数）
			int left = center / 2;
			int right = left + center % 2;
			while(left >= 0 && right < len && s.charAt(left) == s.charAt(right)){
				//结果 + 1
				ans++;
				//向两边扩散
				left--;
				right++;
			}
		}
		return ans;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

但是上面的方法便于理解，但是代码不容易理解，尤其是一些left、right和中心点的关系，中心点的个数

下面我给出一种便于理解的代码：

核心思路：中心扩散，说白了，可以理解成，就是挨个遍历中心点，只不过，中心可能是1个字符也可能是2个字符而已

class Solution{
	public int countSubstrings(String s){
		int ans = 0;
		int len = s.length();
		for(int i = 0; i < len; i++){//遍历回文中心点
			for(int j = 0; j <= 1; j++){//用j来控制中心点是1个字符还是2个字符，j=0,中心是一个点，j=1,中心是两个点(相当于加一)
				int left = i;
				int right = i + j;
				while(left >= 0 && right < len && s.charAt(left) == s.charAt(right)){
					ans++;
					left--;
					right++;
				}
			}
		}
		return ans;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

PS：回文串就三个方法，dp，中心扩散（推荐首选），和马拉车