贪心——区间问题

贪心概述

贪心算法（greedy algorithm，又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解 。

区间做排序和右排序的观察与思考

一般的区间问题都是对于区间之间相交的关系进行策略上的选择
区间做排序和有排序的区别如下图所示

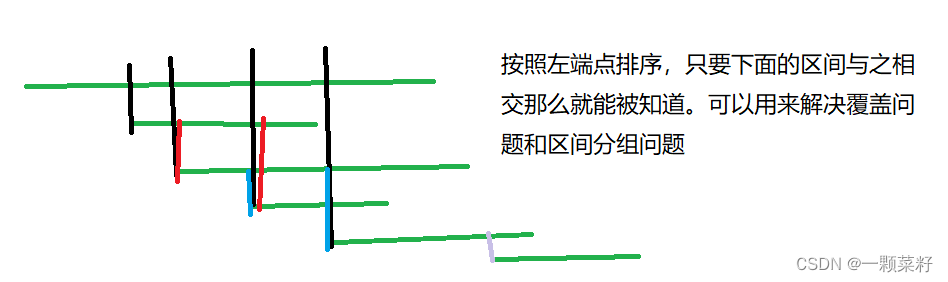
例题

区间选点

给定 N 个闭区间 [ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式
第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示所需的点的最小数量。

数据范围
1≤N≤105,
−109≤ai≤bi≤109
输入样例：
3
-1 1
2 4
3 5
输出样例：
2

1. 思路
   1.将每个区间按右端点从小到大排序
   2. 从前往后依次枚举每个区间
   • 如果当前区间已包含点，则这接pass
   • 否则选择当前区间的右端点
2. 代码

n = int(input())

Range = list()

for i in range(n) :
	Range.append(list(map(int, input().split())))

Range.sort(key = lambda x : x[1])

res = 0
r = - int(2e9)
for i in Range :
	if i[0] > r :
		r = max(r, i[1])
		res += 1

print(res)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

最大不相交区间数量

给定 N 个闭区间 [ai,bi]，请你在数轴上选择若干区间，使得选中的区间之间互不相交（包括端点）。

输出可选取区间的最大数量。

输入格式
第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示可选取区间的最大数量。

数据范围
1≤N≤105,
−109≤ai≤bi≤109
输入样例：
3
-1 1
2 4
3 5
输出样例：
2

1. 思路

   1. 将每个区间按右端点从小到大排序
   2. 从前往后枚举每个区间
      • 如果当前区间与已选择区间有重合部分，则直接pass
      • 否则选择当前区间，记录已选择区间的右端点

2. 代码

n = int(input())

Range = list()

for i in range(n) :
	Range.append(list(map(int, input().split())))

Range.sort(key = lambda x : x[1])

res = 0
r = - int(2e9)
for i in Range :
	if i[0] > r :
		r = max(r, i[1])
		res += 1

print(res)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

区间分组

给定 N 个闭区间 [ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。

输出最小组数。

输入格式
第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示最小组数。

数据范围
1≤N≤105,
−109≤ai≤bi≤109
输入样例：
3
-1 1
2 4
3 5
输出样例：
2

1. 思路

   1. 将所有区间按左端点从小到大排序
   2. 从前往后处理每个区间，判断能否将其放到某个现有组中L[i] > Max_r
      • 如果不存在这样的组，则开新组，然后将其放进去
      • 如果存在这样的组，将其放进去，并更新当前组的Max_r

2. python中heapq模块讲解

from heapq import *
my_data = list(range(10))
my_data.append(0.5)

# 对my_data应用堆属性
heapify(my_data) #将my_data中属性重排序，成堆形状
print('应用堆之后my_data的元素：', my_data)

＃应用堆属性后，新增元素的方法也要使用基于堆的heappush压堆方法，而不再是原来列表的append方法
heappush(my_data, 7.2)
print('添加7.2之后my_data的元素：', my_data)
heappop(my_data) #通过heappop的方式，每次返回堆中的最小值。直到heap为空，报错
nlargest(2,my_data) # 返回最大的两个数
nsmallest(2,my_data) #返回最小的两个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14

3. 代码

from heapq import *

n = int(input())

Range = []
for i in range(n) :
	Range.append(list(map(int, input().split())))

Range.sort()
res = 0
data = []
for i in Range :
	if len(data) == 0 or data[0] >= i[0] :
		heappush(data, i[1])
		res += 1
	else :
		heappop(data)
		heappush(data, i[1])

print(res)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

区间覆盖

给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。

输出最少区间数，如果无法完全覆盖则输出 −1。

输入格式
第一行包含两个整数 s 和 t，表示给定线段区间的两个端点。

第二行包含整数 N，表示给定区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示所需最少区间数。

如果无解，则输出 −1。

数据范围
1≤N≤105,
−109≤ai≤bi≤109,
−109≤s≤t≤109
输入样例：
1 5
3
-1 3
2 4
3 5
输出样例：
2

1. 思路

   1. 将所有区间按照左端点从小到大排序
   2. 从前往后依次枚举每个区间，在所有能覆盖start的区间中选择右端点最大的区间，然后将start更新成右端点

2. 代码

st, ed = map(int, input().split())

n = int(input())

Range = []
for i in range(n) :
	Range.append(list(map(int, input().split())))

Range.sort()
res = 0
is_suc = False
for i in range(n) :
	j = i
	r = - int(2e9)
	while j < n and Range[j][0] <= st :
		r = max(r, Range[j][1])
		j += 1
	
	if r < st :
		res = -1
		break
	res += 1
	
	if r >= ed :
		is_suc = True
		break
	
	st = r
	i = j

if not is_suc :
	res = -1
print(res)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

总结

贪心之难，难如上青天，最好多见，多刷，多熟！