【LeetCode】完全二叉树的节点个数 [M]（递归）

222. 完全二叉树的节点个数 - 力扣（LeetCode）

一、题目

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

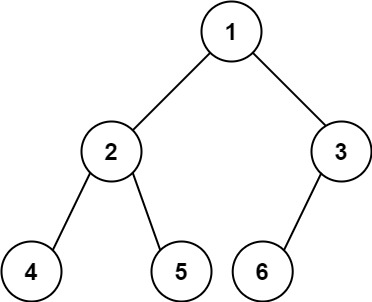
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：
输入：root = []
输出：0

示例 3：
输入：root = [1]
输出：1

提示：

• 树中节点的数目范围是[0, 5 * 104]
• 0 <= Node.val <= 5 * 104
• 题目数据保证输入的树是 完全二叉树

二、代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        // 过滤无效参数
        if (root == null) {
            return 0;
        }
        // mostLeftNodeLevel(root, 1)计算root为根的树总层数为多少
        return process(root, 1, mostLeftNodeLevel(root, 1));
    }
 
    // 当前来到r节点，r节点在level层，总层数是totalLevel
	// 返回r为根的树(必是完全二叉树)，有多少个节点
    public int process(TreeNode r, int level, int totalLevel) {
        // basecase  当前节点r的层数等于总层数，说明该节点就是叶子节点，直接向上返回
        if (level == totalLevel) {
            // 叶子节点上只有一个节点
            return 1;
        }
 
        // 计算当前节点右子树的层数
        int rightTreeMostLeftNodeLevel = mostLeftNodeLevel(r.right, level + 1);
        // 如果右子树的层数小于整棵二叉树的层数，说明此时右子树一定是满的（右子树层数会比整棵二叉树层数少1），左子树不一定满
        if (rightTreeMostLeftNodeLevel < totalLevel) {
            // 右子树为满二叉树，可以直接用公式2^level-1求出来右子树的节点个数，然后去递归求左子树的节点数，然后用右子树节点数+左子树节点数+根节点就等于以r为根的整棵树的节点数
            // 这里rightTreeMostLeftNodeLevel和level都是相对于最初的整颗二叉树的层数，这里要计算的是以r为根节点基础下，r的右子树的层数
            // 所以要用rightTreeMostLeftNodeLevel - level
            return (1 << (rightTreeMostLeftNodeLevel - level)) - 1 + process(r.left, level + 1, totalLevel) + 1;
        // 如果右子树的层数等于整棵二叉树的层数，说明此时左子树一定是满的，右子树不一定满
        } else {
            // 这里用公式求左子树的节点数，然乎递归去求右子树的节点数，然后用右子树节点数+左子树节点数+根节点得到以r为根的整棵树的节点数
            // 这里也要求一下以r作为根节点为计出的左子树层数，totalLevel - level
            return (1 << (totalLevel - level)) - 1 + process(r.right, level + 1, totalLevel) + 1;
        }
    }
 
    // 如果node在第level层，
	// 求以node为头的子树，最大深度是多少
	// node为头的子树，一定是完全二叉树
    public int mostLeftNodeLevel(TreeNode node, int level) {
        // 这里不能写node.left!=0，因为传入的node并没有保证node不是空，如果node是空，就成了调用node.left了
        while (node != null) {
            node = node.left;
            level++;
        }
        // level会多加1层，所以这里要减1
        return level - 1;
    }
}

三、解题思路 

重点要了解完全二叉树和满二叉树的性质，只有满二叉树能通过节点高度计算出确定的节点个数。

左树最左节点的层数就是整棵树的总层数。就去找找头节点右树上的最左节点：

• 如果右树上的最左节点到了最后一层（整棵树的最后一层），就说明左树一定是满的，左树节点数直接公式求出来了。之后就用右子树头节点继续递归（因为右子树不能保证一定是满的）。
• 如果右树上的最左节点没到最后一层，就说明右树一定是满的，但并不能保证左树是不是满的，右树的节点数一个公式就求出来了，之后就用左子树头节点继续递归（因为左子树不能保证一定是满的）。

永远都看右树的最左节点决定你走左还是走右。