LeetCoed617：合并二叉树

要求

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

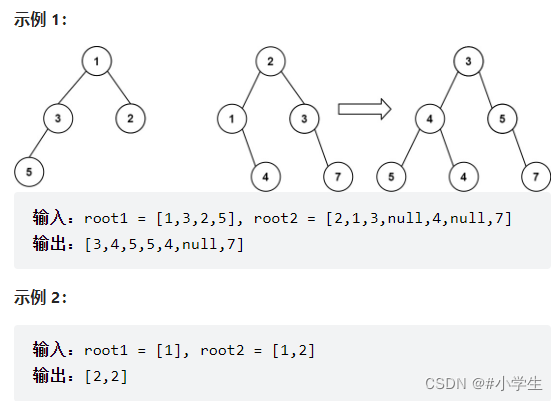
思路

方法一：dfs(深度优先遍历)
从根节点开始同时遍历两个二叉树，并将对应的节点进行合并。

• 如果两个二叉树的对应节点都为空，则合并后的二叉树的对应节点也为空；
• 如果两个二叉树的对应节点只有一个为空，则合并后的二叉树的对应节点为其中的非空节点；
• 如果两个二叉树的对应节点都不为空，则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和，此时需要显性合并两个节点。

public class LeetCode617 {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        //递归终止条件
        if (root1 == null || root2 == null){
            return root1 == null ? root2 : root1;
        }

        //合并树
        TreeNode node = new TreeNode(root1.val + root2.val);
        node.left = mergeTrees(root1.left,root2.left);
        node.right = mergeTrees(root1.right,root2.right);
        return node;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

时间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作，因此被访问到的节点数不会超过较小的二叉树的节点数。

空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。

---

---

方法二：迭代(广度优先算法)
广度优先就需要额外的数据结构来辅助了，我们可以借助栈或者队列来完成。
只要两颗树的左节点都不为 null，就把将他们放入队列中；同理只要两棵树的右节点都不为 null 了，也将他们放入队列中。
然后我们不断的从队列中取出节点，把他们相加。
如果出现 树 1 的 left 节点为 null，树 2 的 left 不为 null，直接将树 2 的 left 赋给树 1 就可以了；同理如果树 1 的 right 节点为 null，树 2 的不为 null，将树 2 的 right 节点赋给树 1。

class Solution {
	public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
	//如果 t1和t2中，只要有一个是null，函数就直接返回
		if(t1==null || t2==null) {
			return t1==null? t2 : t1;
		}
		java.util.LinkedList<TreeNode> queue = new java.util.LinkedList<TreeNode>();
		queue.add(t1);
		queue.add(t2);
		while(queue.size()>0) {
			TreeNode r1 = queue.remove();
			TreeNode r2 = queue.remove();
			r1.val += r2.val;
			//如果r1和r2的左子树都不为空，就放到队列中
			//如果r1的左子树为空，就把r2的左子树挂到r1的左子树上
			if(r1.left!=null && r2.left!=null){
				queue.add(r1.left);
				queue.add(r2.left);
			}
			else if(r1.left==null) {
				r1.left = r2.left;
			}
			//对于右子树也是一样的
			if(r1.right!=null && r2.right!=null) {
				queue.add(r1.right);
				queue.add(r2.right);
			}
			else if(r1.right==null) {
				r1.right = r2.right;
			}
		}
		return t1;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

时间复杂度：O(N)
空间复杂度：O(N)，对于满二叉树时，要保存所有的叶子节点，即 N/2 个节点。