-
B+树的插入、删除和分裂,注意国内教材和国外的对于B+树的定义的不同
B+树
1 国内教材上B+树的定义
一棵 m 阶的B+树满足 (考研教材):
- 每个非叶子结点最多有 m 棵子树(孩子结点)
- 根结点至少有2棵子树 (1层除外),非叶结点至少有 m/2 (向上取整) 棵子树
- 结点的子树的个数与关键字的个数相等: 介于 m/2 (向上取整) ~ m
- 所有的叶子结点包含全部关键字及指向相应记录的指针,叶子结点中将关键字按照大小排序,并且相邻叶子结点按大小连接
- 所有非叶结点中仅包含它的各个子结点中的关键字的最大值及指向其子结点的指针。
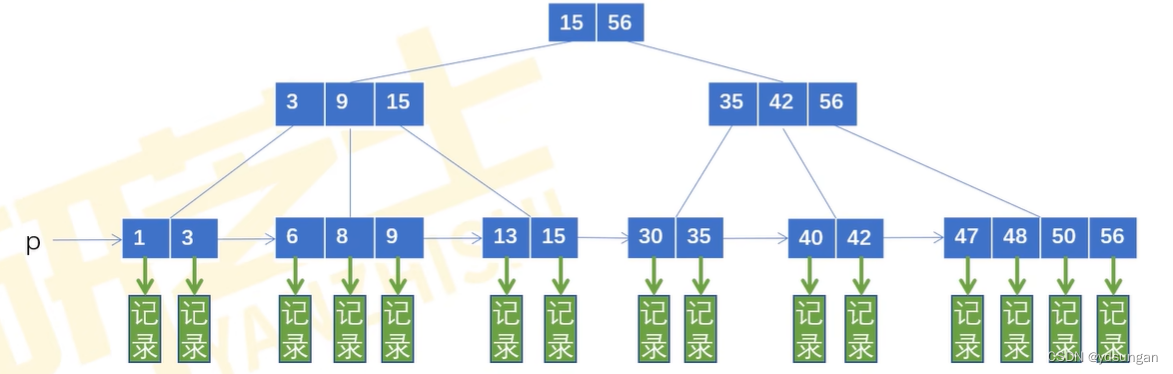
对于中间结点来说,比如结点 [3, 9, 15],它们的子树的范围分别是:<=3,3< x<=9,9< x
2 国外关于B+树的定义
动态演示:https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
其实B+树和B树的根本区别就是:B+树的中间结点不存储记录。国内教材和国外关于一个中间结点有 m 个元素时,它的子结点是 m 还是 m+1 是不同定义的,如果不是数据结构考试而在实际开发中,我觉得这是无关要紧的。在上面的动画演示当中一个m阶的B+树,中间结点和叶子结点里面的元素均最多m-1个,也就是当中间结点或者叶子结点的元素达到m个时,就需要分裂,中间结点的子树最多m个。(这和国内的规定是不同的。)
国外的关于B+树更多的是:m阶的B+树,根节点及中间结点和叶子结点均最多只有m-1个元素,最多有m个子树。最少有 ceil(m/2) - 1个元素。 如下图是一个3阶B+树。

由动态演示得出:B+树无论怎么倾斜地插入元素,始终使得B+树的所有的叶子结点都在同一层。即B+树永远不会倾斜地增长,所有叶子结点永远在同一层
3 B+树的优势
一般使用B+树作为索引(vs B-Tree)的原因:传统的磁盘系统中将一个B+树的中间结点大小设置为一个磁盘块 (4KB) 的大小,由于B+树的结点不包含记录值,所以一个磁盘块可以存储更多的元素,使得B+树更矮,读取磁盘的操作更少,查找更快。
4 B+树的插入
参考:https://www.javatpoint.com/b-plus-tree
按照国外的B+树的规定:
step1:找到元素属于的叶结点,插入新元素。(注意:是从根结点一层一层往下查找,直到其所属的叶子结点再插入新元素)
step2:如果叶子结点空间不满足了,如5阶的B+树中的叶子结点有5个元素,那么将分裂叶子结点,将叶子结点的中间元素向上提到父结点。
step3:如果一个中间结点空间不满足了,分裂结点,将里面的中间元素向上提到父结点。
如下图所示:

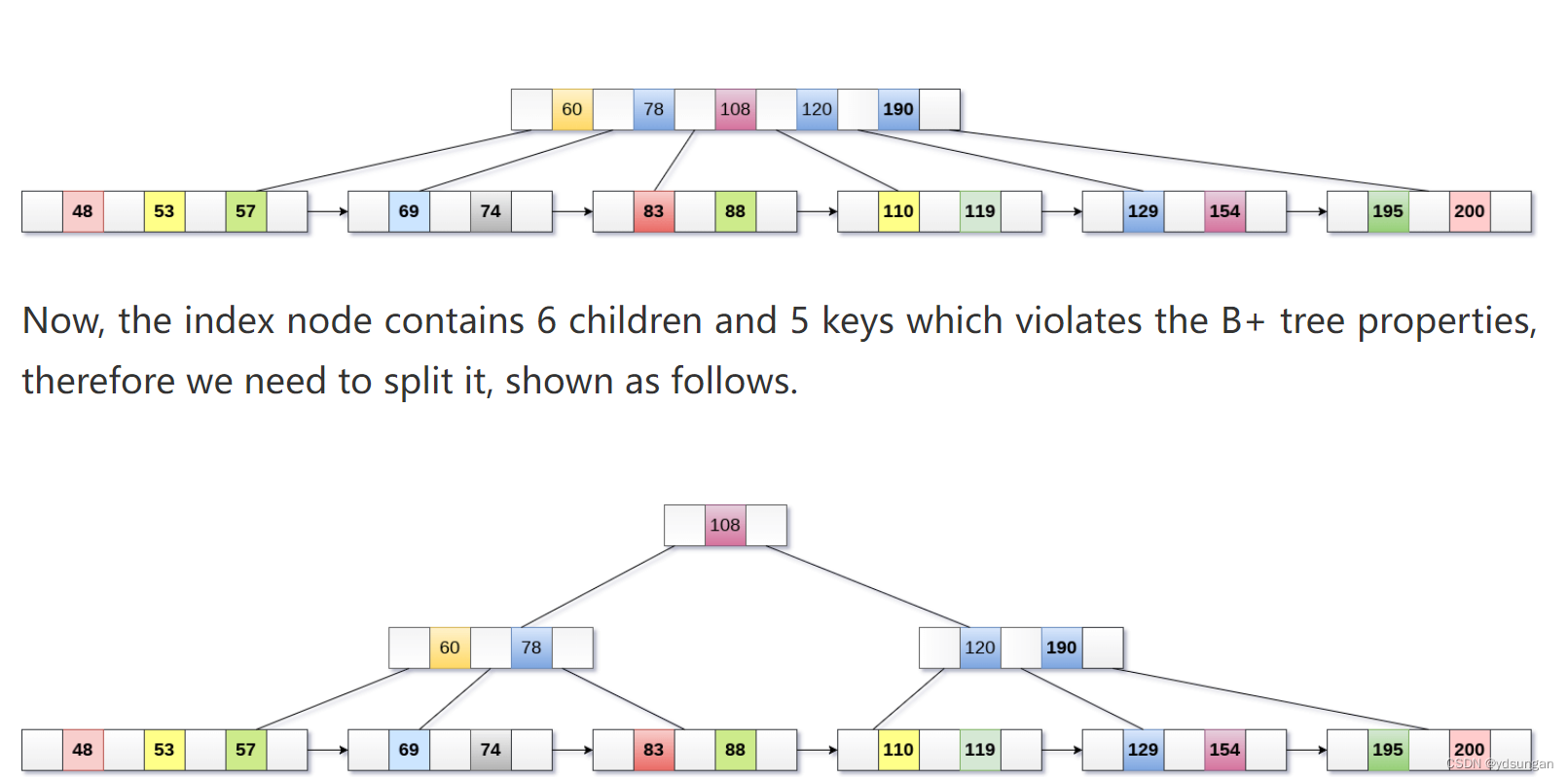
5 B+树的删除
注意:5阶B+树中间结点最少有 ceil(m/2) - 1 = 2个元素,最多有m-1 = 4个元素


6 B+树的分裂总结
B+树的详细分裂过程见:4 B+树的插入。
B+树的分裂是从叶子结点开始的,接着就是其父结点,一层一层的往上分裂,直到中间结点可以容纳为止。每个结点分裂(包括中间结点、叶子结点)都是从结点的元素中选取一个中间大小的元素,这个元素很关键,这个元素是分裂元素,需要将这个元素向上提!提到其父结点中!而原来结点以这个分裂元素为中心,分裂成俩个兄弟结点,分裂挂在父结点中的分裂元素的俩边!
-
相关阅读:
gxhxjxizj
浅谈Java内部锁synchronized
Springcloud Alibaba详细入门教程(一)
关于Docker中容器之间互相访问问题
01 java开始 & 02 java常见问题
MQ---第一篇
信号面试题
【计算机毕业设计】094图书馆自习室座位预约管理微信小程序
【JavaScript】axios
勒索病毒最新变种.360勒索病毒来袭,如何恢复受感染的数据?
- 原文地址:https://blog.csdn.net/weixin_45482422/article/details/127666526