【异常检测】【PaDiM】论文简单梳理与代码实现

every blog every motto: There’s only one corner of the universe you can be sure of improving, and that’s your own self.
https://blog.csdn.net/weixin_39190382?spm=1010.2135.3001.5343

0. 前言

相比之前的SPADE又进了一步，还是很不错的一篇文章

1. 正文

论文： https://arxiv.org/abs/2011.08785
时间： 2020
作者： Thomas Defard, Aleksandr Setkov, Angelique Loesch, Romaric Audigier
单位： Universite Paris-Saclay

1.1 整理流程

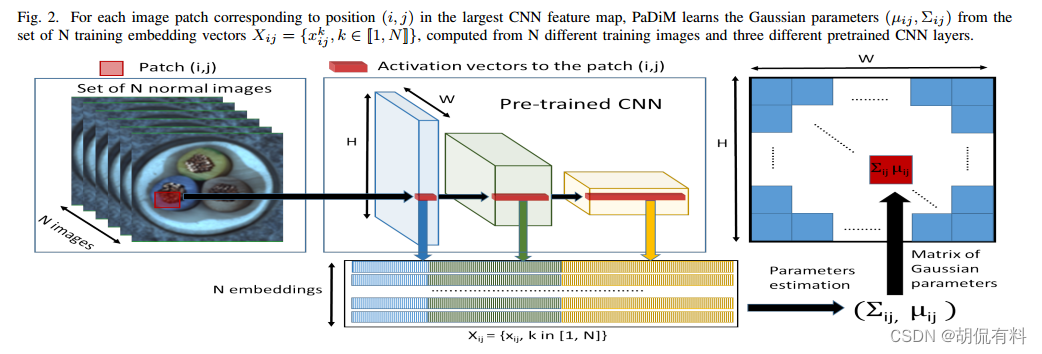
结果：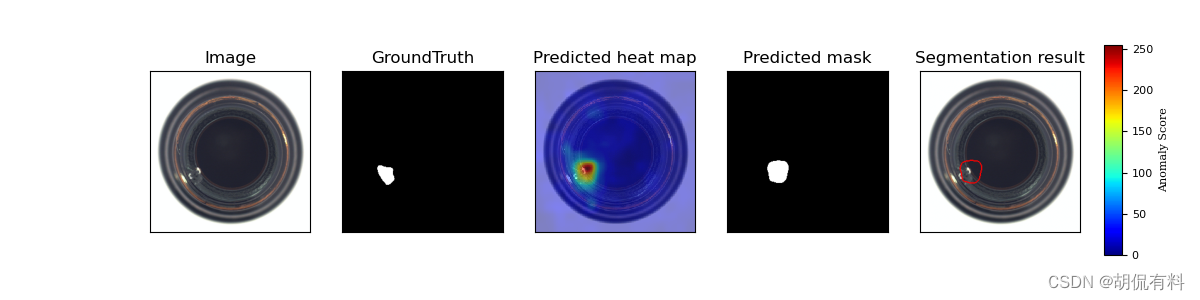

a. embedding extraction

使用resnet作为特征提取网络，从网络中提取特定的三层（和SPADE一样用到了钩子函数），训练集提取到的三个特征图shape为（B,C,H,W）：

• （209，256，56，56）
• （209，512，28，28）
• （209，1024，14，14）
  然后将三个特征图在通道方向上堆叠（类似垒大饼，或是垒色子），当然，垒之前需要将特征图切割到相同大小，这里用到了unfold，以及恢复时fold。可参考unfold和fold直观理解

如下图所示，颜色相同表示数据相同（因为三个特征图的大小不同，所以会出现这个情况）。

三个通特征图合并以后的shape为：（209，1792，56，56）
在随机选择500个通道（论文实验表明，随机选取比PCA效果好），其shape：（209，550，56，56）

b. learning of the normality

图像的像素假设是多维高斯分布，所以会求出均值和协方差。因为是像素级处理，会将上面提取的embedding vetor进行处理，shape变换：
（209，550，56，56） -> （209，550，56*56），
可以理解拉成一条直线（209，550，3136）。

求batch中所有图片（对应像素的均值）：（550，3136），
协方差：（550，550，3136）
一个像素，含有若干通道，上面的通道数为550，可以理解为一个长度为550向量

至此，我们将训练集（全为正常图片）的正常图片每个像素，都用多维高斯分布进行了表示，即均值和协方差表示

c. Inference : computation of the anomaly map

在上一步中，我们得到了正常图像的表示，在推理过程中，我们需要计算测试图片和训练图片之间的“距离”。距离计算使用的马氏距离，具体可参考马氏距离，点到一个分布的计算

距离越远（数值越大）表示异常概率越大。

1. 2 代码

a. 训练集特征提取

def extract_train_feature(train_dataloader, args, class_name, model, idx, outputs):
    """提取是训练集特征，保存的是处理后的均值和协方差"""

    train_outputs = OrderedDict([('layer1', []), ('layer2', []), ('layer3', [])])
    # extract train set features
    train_feature_filepath = os.path.join(args.save_path, 'temp_%s' % args.arch, 'train_%s.pkl' % class_name)
    if not os.path.exists(train_feature_filepath):
        for (x, _, _) in tqdm(train_dataloader, '| feature extraction | train | %s |' % class_name):
            # model prediction
            with torch.no_grad():
                p = model(x.to(device))
            # get intermediate layer outputs
            for k, v in zip(train_outputs.keys(), outputs):
                train_outputs[k].append(v.cpu().detach())
            # initialize hook outputs
            outputs.clear()
        for k, v in train_outputs.items():
            train_outputs[k] = torch.cat(v, 0)

        # Embedding concat
        embedding_vectors = train_outputs['layer1']  # (209,256,56,56)
        for layer_name in ['layer2', 'layer3']:
            embedding_vectors = embedding_concat(embedding_vectors, train_outputs[layer_name])

        # randomly select d dimension (209,1792,56,56) -> (209,550,56,56)
        embedding_vectors = torch.index_select(embedding_vectors, 1, idx)
        # calculate multivariate Gaussian distribution
        B, C, H, W = embedding_vectors.size()
        # (209,550,56,56) -> (209,550,3136)
        embedding_vectors = embedding_vectors.view(B, C, H * W)
        # (550,3136)
        mean = torch.mean(embedding_vectors, dim=0).numpy()
        cov = torch.zeros(C, C, H * W).numpy()  # (550,550,3136)
        I = np.identity(C)
        for i in range(H * W):  # 对角线上加一个值，使其满秩可逆
            # cov[:, :, i] = LedoitWolf().fit(embedding_vectors[:, :, i].numpy()).covariance_
            cov[:, :, i] = np.cov(embedding_vectors[:, :, i].numpy(), rowvar=False) + 0.01 * I
        # save learned distribution
        train_outputs = [mean, cov]
        with open(train_feature_filepath, 'wb') as f:
            pickle.dump(train_outputs, f)
    else:
        print('load train set feature from: %s' % train_feature_filepath)
        with open(train_feature_filepath, 'rb') as f:
            train_outputs = pickle.load(f)

    return train_outputs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

b. 测试集特征提取

def extract_test_features(test_dataloader, model, class_name, outputs):
    test_outputs = OrderedDict([('layer1', []), ('layer2', []), ('layer3', [])])

    gt_list = []
    gt_mask_list = []
    test_imgs = []
    temp_x = None
    # extract test set features
    for (x, y, mask) in tqdm(test_dataloader, '| feature extraction | test | %s |' % class_name):
        if temp_x == None:
            temp_x = x
        test_imgs.extend(x.cpu().detach().numpy())
        gt_list.extend(y.cpu().detach().numpy())
        gt_mask_list.extend(mask.cpu().detach().numpy())
        # model prediction
        with torch.no_grad():
            _ = model(x.to(device))
        # get intermediate layer outputs
        for k, v in zip(test_outputs.keys(), outputs):
            test_outputs[k].append(v.cpu().detach())
        # initialize hook outputs
        outputs.clear()
    for k, v in test_outputs.items():
        test_outputs[k] = torch.cat(v, 0)

    # Embedding concat,通道方向上拼接
    embedding_vectors = test_outputs['layer1']  # (83,256,56,56)
    for layer_name in ['layer2', 'layer3']:
        embedding_vectors = embedding_concat(embedding_vectors, test_outputs[layer_name])

    return embedding_vectors, gt_list, gt_mask_list, test_imgs, temp_x

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

c. 距离计算

        for i in range(H * W):
            # train_outputs:[mean,con] mean:[550,3316],cov:[550,550,3136]
            mean = train_outputs[0][:, i]  # [550,]
            conv_inv = np.linalg.inv(train_outputs[1][:, :, i])  # 协方差逆阵 （550，550）
            # 3136 * [(550,)*(550,550)*(550,)] -> (550,3136)
            dist = [mahalanobis(sample[:, i], mean, conv_inv) for sample in embedding_vectors]
            dist_list.append(dist)
        # 3136*(83,) -> (83,56,56)
        dist_list = np.array(dist_list).transpose(1, 0).reshape(B, H, W)  # (83,56,56)
1
2
3
4
5
6
7
8
9

1.3 小结

通俗理解：
将训练集中每一个像素用一个分布表示（多维高斯分布），然后计算，测试集中每个像素到训练集中对应像素的距离。因为训练集是正常图片，所以测试图片离训练集（正常图片）越远，表示异常的概率越大。所以用距离表示异常的得分。

感觉还是挺有意思的，

1. 用多维高斯分布表示像素
2. 计算距离（马氏距离）

之前SPADE用KNN找到最近的几张图片，相同点都是用到了距离的计算，但是对“距离”的看法有所不同

完整代码：PaDiM，欢迎star

参考

[1] https://blog.csdn.net/weixin_39190382/article/details/127656042?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22127656042%22%2C%22source%22%3A%22weixin_39190382%22%7D
[2] https://blog.csdn.net/qq_41804812/article/details/125193330
[3] https://blog.csdn.net/sinat_24899403/article/details/111032279