数的范围---二分法

题目描述

给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。如果数组中不存在该元素，则返回“-1 -1”。

例如

num = [1,2,2,3,3,4];

• 查找3

        返回结果：3, 4

• 查找4

        返回结果：5, 5

• 查找5

        返回结果：-1, -1

这里以 查找3 为例进行讲解。

假设此时的情景为，需要我们找到第一个>=3的数字，试想一下，如果能把整个区间分了两半，左边是<3的区间，右边是>=3的区间 如图:

那么右区间的第一个点，就是我们找到的符合>=3的第一个数字,将区间分为两半，是不是非常清晰！

        int l = -1;
        int r = q.length;
        while (l + 1 != r) {
            int mid = (l + r) >> 1;
            if (q[mid] >= x) {
                r = mid;
            } else {
                l = mid;
            }
            // 此时r 就是第一个3出现的位置
        }

【同理】第二个3出现的位置为

            l = -1;
            r = q.length ;
            while (l + 1 != r) {
                int mid = (l + r ) >> 1;
                if (q[mid] <= x) {
                    l = mid;
                } else {
                    r = mid;
                }
            }
            System.out.println(l);

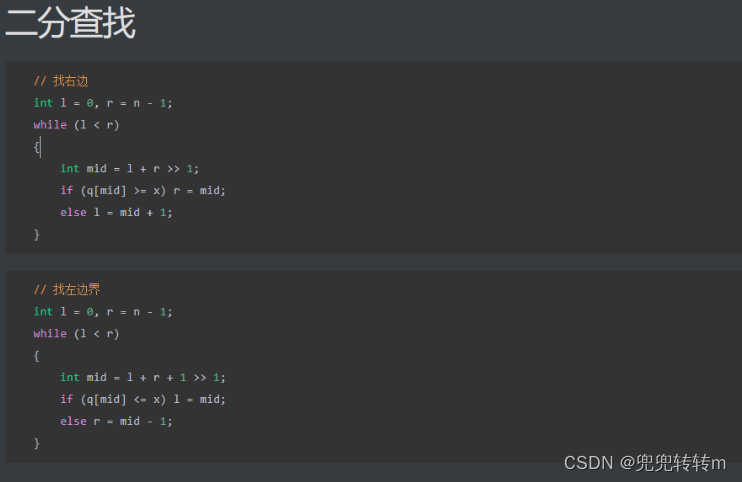
【代码】最后给出两种实现--但是推荐采用binaryModel函数

package algorithm;
 
import java.util.Scanner;
 
public class BinaryModel {
    public static void main(String[] args) {
        int[] q = {1, 2, 2, 3, 3, 4};
        binarySort(q, 5);
 
    }
 
    public static void binarySort(int[] q, int x) {
        int l = 0;
        int r = q.length - 1;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (q[mid] >= x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        if (q[r] != x) {
            System.out.println("-1 -1");
        } else {
            System.out.print(r + " ");
            l = 0;
            r = q.length - 1;
            while (l < r) {
                int mid = (l + r + 1) >> 1;
                if (q[mid] <= x) {
                    l = mid;
                } else {
                    r = mid - 1;
                }
            }
            System.out.println(l);
        }
 
    }
 
    public static void binaryModel(int[] q, int x) {
        int l = -1;
        int r = q.length;
        while (l + 1 != r) {
            int mid = (l + r) >> 1;
            if (q[mid] >= x) {
                r = mid;
            } else {
                l = mid;
            }
            // 此时r 就是第一个3出现的位置
        }
        if (q[r] != x) {
            System.out.println("-1 -1");
        } else {
            System.out.print(r + " ");
            l = -1;
            r = q.length ;
            while (l + 1 != r) {
                int mid = (l + r ) >> 1;
                if (q[mid] <= x) {
                    l = mid;
                } else {
                    r = mid;
                }
            }
            System.out.println(l);
        }
 
    }
}