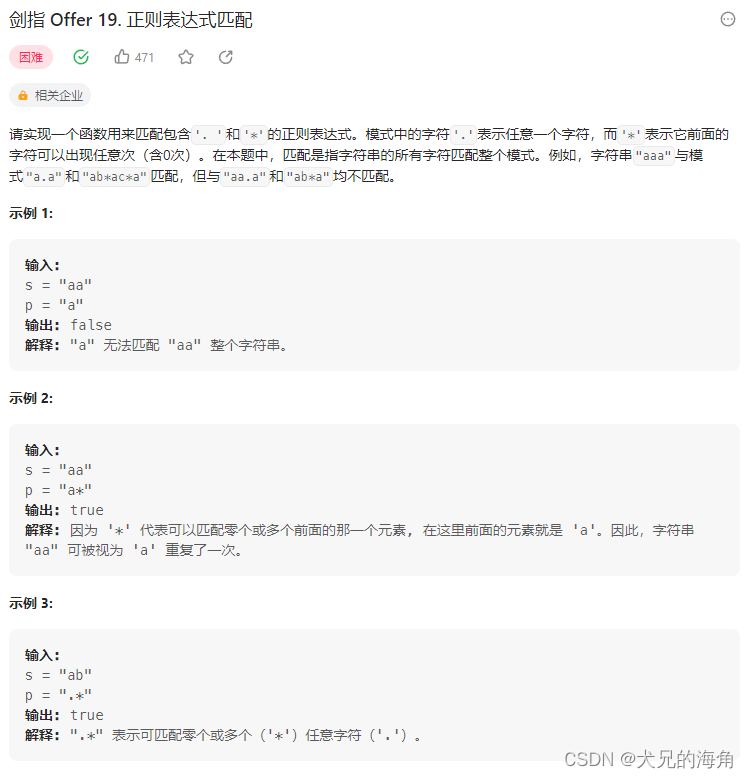
LeetCode-剑指19-正则表达式匹配

1、递归

我们可以通过选取当前字符串的子串来递归的匹配当前的表达式：1、若表达式为空而字符串不为空返回false；2、若表达式的第二位为“*”，则存在两种可能，一种是第一位匹配，我们继续匹配第二位；第二种是第一位不匹配，此时我们从表达式的第三位开始进行匹配；3、若表达式的第二位不为“*”，我们继续匹配字符串和表达式的第二位。

class Solution {
public:
    bool isMatch(string s, string p){
        if (p.empty())  return s.empty();
        bool first_match = !s.empty() && (s[0] == p[0] || p[0] == '.');
        if (p.size() >= 2 && p[1] == '*')
            return (first_match && isMatch(s.substr(1), p)) || isMatch(s, p.substr(2));
        else
            return first_match && isMatch(s.substr(1), p.substr(1));
    }
};
1
2
3
4
5
6
7
8
9
10
11

2、动态规划法

我们可以利用数组$f[i][j]$来记录字符串的前i位与表达式的前j位的匹配情况。我们可以获得状态转化方程如下： f [ i ] [ j ] = { 若 p [ j ] ≠ ′ ∗ ′ ， { f [ i − 1 ] [ j − 1 ] ，s[i]与p[j]相匹配 f a l s e ，s[i]与p[j]不匹配 若 p [ j ] = ′ ∗ ′ ， { f [ i − 1 ] [ j ] o r f [ i ] [ j − 1 ] ，s[i]与p[j-1]相匹配 f [ i ] [ j − 2 ] ，s[i]与p[j]不匹配

f[i][j]=⎩ ⎨ ⎧​若p[j]=′∗′，{f[i−1][j−1]，s[i]与p[j]相匹配false，s[i]与p[j]不匹配​若p[j]=′∗′，{f[i−1][j]orf[i][j−1]，s[i]与p[j-1]相匹配f[i][j−2]，s[i]与p[j]不匹配​​​

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size();
        int n = p.size();

        auto matches = [&](int i, int j) {
            if (i == 0) {
                return false;
            }
            if (p[j - 1] == '.') {
                return true;
            }
            return s[i - 1] == p[j - 1];
        };

        vector<vector<int>> f(m + 1, vector<int>(n + 1));
        f[0][0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                if (p[j - 1] == '*') {
                    f[i][j] |= f[i][j - 2];
                    if (matches(i, j - 1)) {
                        f[i][j] |= f[i - 1][j];
                    }
                }
                else {
                    if (matches(i, j)) {
                        f[i][j] |= f[i - 1][j - 1];
                    }
                }
            }
        }
        return f[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36