-
【每日一题】子数组最大异或和
数组异或和的定义:把数组中所有数异或起来得到的值。
给定一个整型数组:arr,其中可能有正、有负、有零,求其子数组的最大异或和
【举例】
arr = 【3】
数组中只有 1 个数,所以只有一个子数组,就是这个数组本身,最大异或和为 3
arr = 【3,-28,-29,2】
子数组有很多,但是【-28,-29】这个子数组的异或和为 7,是所有子数组中最大的。
分析:
异或和没有单调性。两个小的数的异或和可能比两个大数的异或和大。
解法一:暴力算法
对每一个以 i 为开始和以 j 为结尾的子数组,进行异或和计算,获取全局最大的异或和,就是答案。
时间复杂度: O ( N 3 ) O(N^3) O(N3)
时间复杂度:O(1)
import sys def max_xor(arr): if not arr: return 0 res = -sys.maxsize for i in range(len(arr)): for j in range(i, len(arr)): # 窗口:arr[i,j+1],计算窗口内数据的异或和 xor = 0 for k in range(i, j + 1): xor ^= arr[k] res = max(res, xor) return res- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
解法二:前缀异或和
前缀和的性质:
- 归零率:A ^ A = 0
- 恒等率:A ^ 0 = A
根据上述两个性质可以推导出:
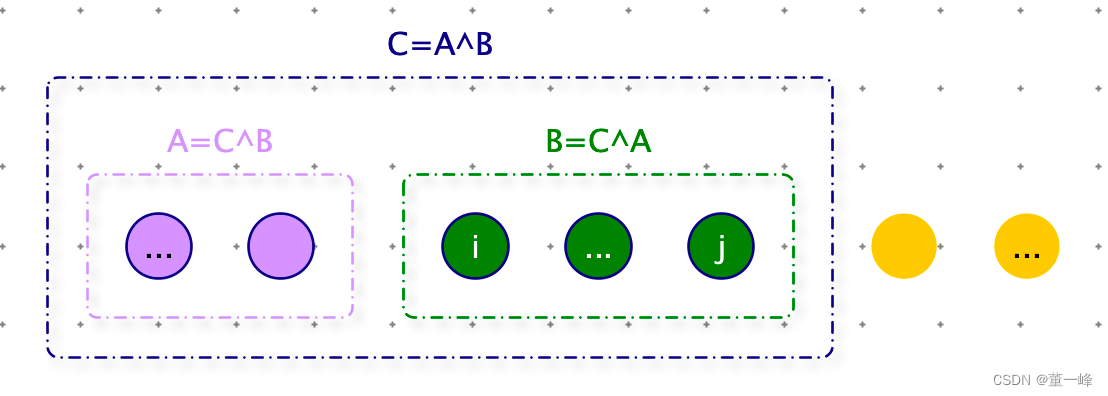
C = A ⊕ B ⟹ C ⊕ A = A ⊕ B ⊕ A ⟹ C ⊕ A = B ⊕ 0 ⟹ A ⊕ C = B C = A \oplus B \Longrightarrow \\ C \oplus A = A \oplus B \oplus A \Longrightarrow \\ C \oplus A = B \oplus 0 \Longrightarrow \\ A \oplus C = B C=A⊕B⟹C⊕A=A⊕B⊕A⟹C⊕A=B⊕0⟹A⊕C=B
根据前缀异或和可以计算出任意子数组的异或和。
时间复杂度: O ( N 2 ) O(N^2) O(N2)
时间复杂度:O(N)
def max_xor1(arr): if not arr: return 0 # 前缀异或和 prefix_sum = [arr[0]] for i in range(1, len(arr)): prefix_sum.append(arr[i] ^ prefix_sum[-1]) res = -sys.maxsize for i in range(len(arr)): s = 0 if i == 0 else prefix_sum[i - 1] for j in range(i, len(arr)): # 窗口:arr[i,j+1] xor = prefix_sum[j] ^ s res = max(res, xor) return res- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
解法三:前缀树 + 贪心
由解法二可知: C = A ⊕ B ⟹ B = C ⊕ A C = A \oplus B \Longrightarrow B = C \oplus A C=A⊕B⟹B=C⊕A
即: a r r [ 2...5 ] = a r r [ 0...5 ] ⊕ a r r [ 0...2 ] arr[2...5] = arr[0...5] \oplus arr[0...2] arr[2...5]=arr[0...5]⊕arr[0...2]
- arr[0…5] 与 0 结合表示:arr[0…5] 子数组的异或和
- arr[0…5] 与 arr[0] 结合表示:arr[1…5] 子数组的异或和
- arr[0…5] 与 arr[0…1] 结合表示:arr[2…5] 子数组的异或和
- arr[0…5] 与 arr[0…2] 结合表示:arr[3…5] 子数组的异或和
- …
与谁结合异或和大,应对的子数组就是要找的子数组。
目前不知道 arr[0…5] 选择哪个?在解法二中是枚举尝试,我们现在想通过前缀树构建一种规则(贪心策略)来加速寻找最佳结合子数组。

贪心策略:在 arr[0…j] 选择 arr[ 0…i ] 结合过程中,优先迎合高位变成 1(高位为1,对应值更大)。
如下图:arr[0…j] 的异或和的二进制形式【0,1,1,0】,从高位A逐一匹配。由于 0 ^ 1 = 1,所以选择 1 的分支( A --> C ), 在 F 位置,虽然最期待走的路径是 0 ,但是没有 0 路径所以只能走 1 路径。整条路径【1,0,1,1】 就是 arr[0…j] (【0,1,1,0】)最佳结合的子数组对应的异或和。【0,1,1,0】^ 【1,0,1,1】= 【1,0,1,1】此时【1,0,1,1】 就是的返回结果 arr[0…j]。
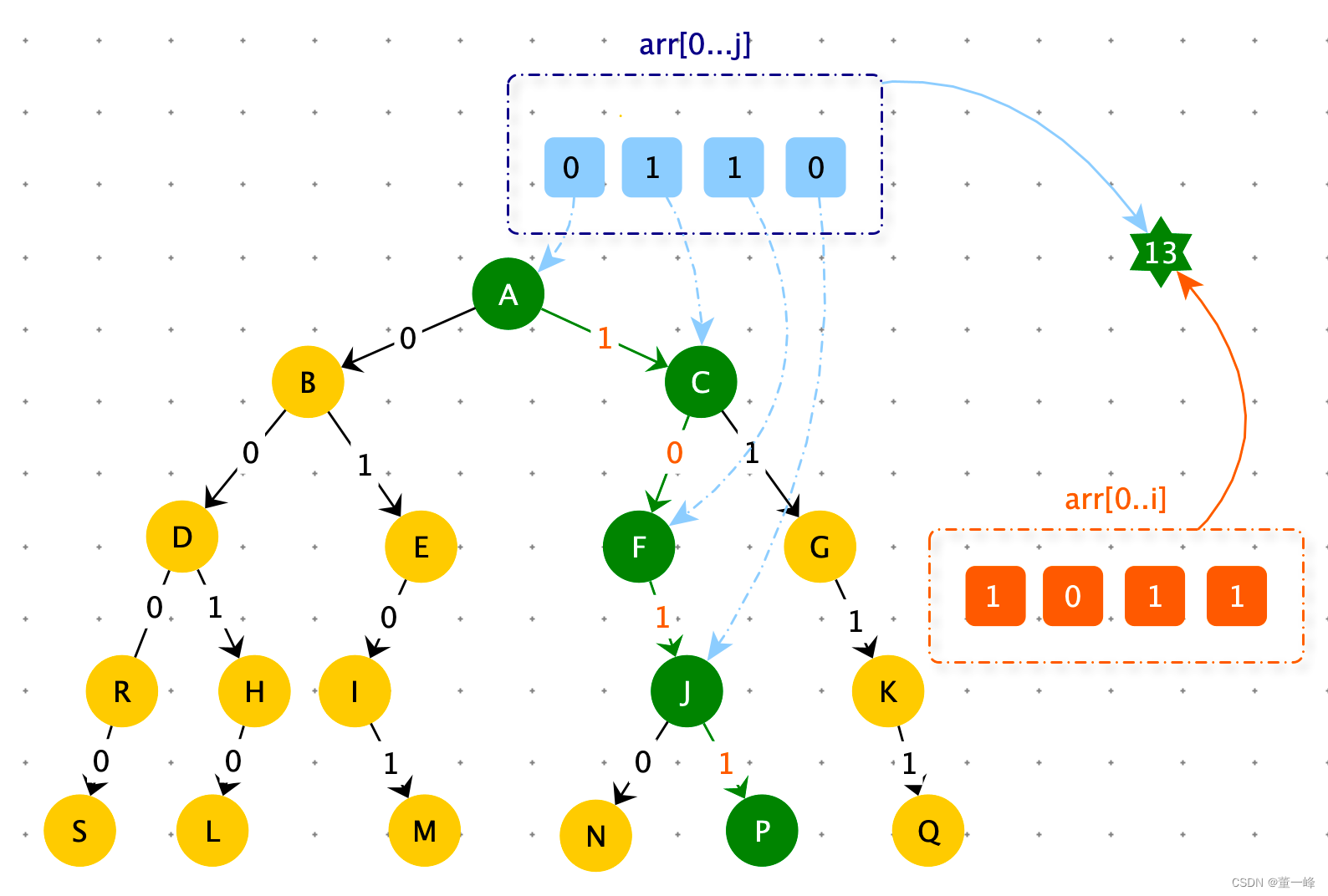
前缀树
# 将所有的前缀异或和,加入到 NumTrie,并按照前缀树组织 class NumTrie: def __init__(self): self.root = Node() def add(self, num): cur = self.root # move 向右位移多少位 for move in range(31, -1, -1): # 获取对应位上的数字(0 或者 1) path = (num >> move) & 1 cur.nexts[path] = cur.nexts[path] if cur.nexts[path] else Node() cur = cur.nexts[path] # num 最希望遇到的路径,结果返回:最大的异或和 # 时间复杂度:O(32) def max_xor(self, num): cur = self.root # 返回值(num ^ 最优选择) res = 0 for move in range(31, -1, -1): # 获取对应位上的数字(0 或者 1) path = (num >> move) & 1 # sum 该位的状态,最期待的路径(如果sum 位是0,期待path =1,否则 path = 0) # 注意:如果是符号位是 1(负数),期待 path = 1,异或后是 0(正数) # 如果是符号位是 0(正数),期待 path = 0,异或后是 0(正数) best = path if move == 31 else path ^ 1 # 最期待走的路径 --> 实际路径 best = best if cur.nexts[best] else best ^ 1 # 注意:本代码是 python,左移 31 位不会变为负数,python 会将 int 转为 long 变为更大的数 # 如果是 java:res |= (path ^ best) << move tmp = 1 if move == 31 and num < 0: tmp = -1 res |= tmp * (path ^ best) << move cur = cur.nexts[best] return res- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
时间复杂度: O ( N ) O(N) O(N)
时间复杂度:O(N)
def max_xor2(arr): if not arr: return 0 res = -sys.maxsize trie = NumTrie() trie.add(0) # 一个数没有时,异或和为 0 xor = 0 for i in range(len(arr)): # xor 等于 0 ~ i 异或和 xor ^= arr[i] # trie 装着所有:一个数也没有(0),0~1,0~2,0~3...0~i-1 的异或和 res = max(res, trie.max_xor(xor)) trie.add(xor) return res- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
对数器
import random def check(): max_value = 10 for i in range(100): arr = [int(random.random() * max_value) - int(random.random() * max_value) for _ in range(int(random.random() * max_value))] res = max_xor(arr) res1 = max_xor1(arr) res2 = max_xor2(arr) if res != res1 or res != res2: print(i, "ERROR", arr, "res=", res, "res1=", res1, "res2=", res2) print("NICE")- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
-
相关阅读:
Spring-bean
每日学术速递5.28
Spring Boot 笔记 021 项目部署
计算机组成原理习题课第四章-3(唐朔飞)
pip工具的使用:基本+高级用法
Linux部署Tomcat踩的坑以及解决方案【8080无法访问、日志显示XX端口被占用、修改默认端口、无法提供安全连接】
迷你内裤洗衣机排名前十名:2024年十大口碑一流内衣洗衣机推荐
Java语言基础第二天
动态通讯录及程序保存在文件中
Springboot物资发放管理系统
- 原文地址:https://blog.csdn.net/junxinsiwo/article/details/127649655
