-
时间序列预测算法梳理(Arima、Prophet、Nbeats、NbeatsX、Informer)
时间序列预测算法梳理(Arima、Prophet、Nbeats、NbeatsX、Informer)
Arima
1. 算法原理
自回归滑动平均(Autoregressive integrated moving average,ARIMA)模型由Box和Jenkins于1970年提出。他们认为某些非平稳序列中,某一部分与其他部分相似,而这种同质性可经d阶差分后就可以成为平稳序列,成为混合自回归-滑动平均过程。那么该非平稳序列为ARIMA模型,用 表示。其中,p表示自回归AR的阶次,q表示移动平均MA的移动平均项数,而d是变成平稳序列时所做的差分阶次。通式如下所示。

若d=0,则为一个平稳过程。而d不为0时,需要选择合适的阶次d,进行差分处理,并通过自相关图或者单位根检验进行平稳性验证。2. 算法实现
(1)观察时序的平稳性和随机性
1: 数据具有周期性、长期增长的趋势,并非在某一个常数上下波动,因此主观判断该序列为非平稳时间序列。(非平稳时间序列,在消去其局部水平或者趋势之后,其显示出一定的同质性,也就是说,此时序列的某些部分 与其它部分很相似。)
2: 对非平稳序列进行差分处理,变成平稳序列。
(2)选择具体的模型
1: 一阶差分后的时序图没有明显的线性趋势,观察自相关图ACF和偏自相关图PACF
2: 数据具有周期性,现在按照周期数再进行差分(进行12阶差分后)
(3)拟合模型
1: 使用极大似然估计,拟合ARIMA模型
(4)根据选定模型进行预测
1: 根据选定模型进行预测
预测未来6个月的销售值,设置上下95%的置信区间
(5)模型评价
1: 判断预测误差是否是平均值为零且方差为常数的正态分布;
2: 对模型的残差进行独立性检验(是否相关)Prophet
1. 优点
Facebook 所提供的 prophet 算法不仅可以处理时间序列存在一些异常值的情况,也可以处理部分缺失值的情形,还能够几乎全自动地预测时间序列未来的走势。从论文上的描述来看,这个 prophet 算法是基于时间序列分解(分解成:季节项+趋势项+剩余项+节假日的效应)和机器学习的拟合(L-BFGS 方法)来做的,其中在拟合模型的时候使用了pyStan这个开源工具,因此能够在较快的时间内得到需要预测的结果。
2. 算法实现
时间序列分解+机器学习拟合。
(1)时间序列分解:
时间序列分成几个部分:季节项+趋势项+剩余项+节假日的效应

- 趋势项模型 :
趋势项有两个重要的函数,一个是基于逻辑回归函数(logistic function)的,另一个是基于分段线性函数(piecewise linear function)的。 - 季节性趋势(周期性的变化):
时间序列通常会随着天,周,月,年等季节性的变化而呈现季节性的变化,也称为周期性的变化。在数学分析中,区间内的周期性函数是可以通过正弦和余弦的函数来表示 - 节假日效应:
由于每个节假日对时间序列的影响程度不一样。因此,不同的节假日可以看成相互独立的模型,并且可以为不同的节假日设置不同的前后窗口值,表示该节假日会影响前后一段时间的时间序列。
(2)时间序列分解:机器学习拟合:
在 Prophet 里面,作者使用了 pyStan 这个开源工具中的 L-BFGS 方法来进行函数的拟合。L-BFGS是解无约束非线性规划问题最常用的方法,具有收敛速度快、内存开销少等优点,L-BFGS和梯度下降、SGD干的同样的事情,但大多数情况下收敛速度更快。
3.算法api实现(fbprophet调api)
fbprophet 所需要的时间序列:第一列的名字是 ‘ds’, 第二列的名称是 ‘y’。通过 prophet 的计算,可以计算出 yhat,yhat_lower,yhat_upper,分别表示时间序列的预测值,预测值的下界,预测值的上界。
- API计算步骤:
1: 输入已知的时间序列的时间戳和相应的值;
2: 输入需要预测的时间序列的长度;
3: 输出未来的时间序列走势。
4: 输出结果可以提供必要的统计指标,包括拟合曲线,上界和下界等。
Nbeats
1. Nbeats优点
Nbeats开创了一个全新的时间序列预测backbone,仅通过全连接实现时间序列预测。Nbeats的核心思路是,通过多层全连接进行时间序列分解,每层拟合时间序列部分信息(之前层拟合的残差)。其中每个block的输入,是上一层block的输入减去上一层block的输出。通过这种方式,模型每层需要处理的是之前层无法正确拟合的残差,也起到了一个将时间序列进行逐层分解,每层预测时间序列一部分的作用。
2. Nbeats模型结构
整个模型包括多个stack,每个stack包括多个block。每个block是Nbeats的最基础结构模块,由多个全连接层组成。每个block包含两个主要部分:第一个部分将输入的时间序列映射成expansion coefficients,第二部分将expansion coefficients映射回时间序列。(内部学习过程发生在块内部,并帮助模型捕获局部时间特征。外部学习过程发生在堆叠层,帮助模型学习所有时间序列的全局特征。)expansion coefficients可以理解为:存储了时间序列内在的信息形成的一个低维向量。在模型实现上,其实就是一个向量映射过程:将输入的时间序列(维度为length)映射成低维向量(维度为dim),第二部分再将其映射回时间序列(长度为length)。每个模块会生成两组expansion coefficients膨胀系数,一组用来预测未来(forecast),另一组用来预测过去(backcast)。
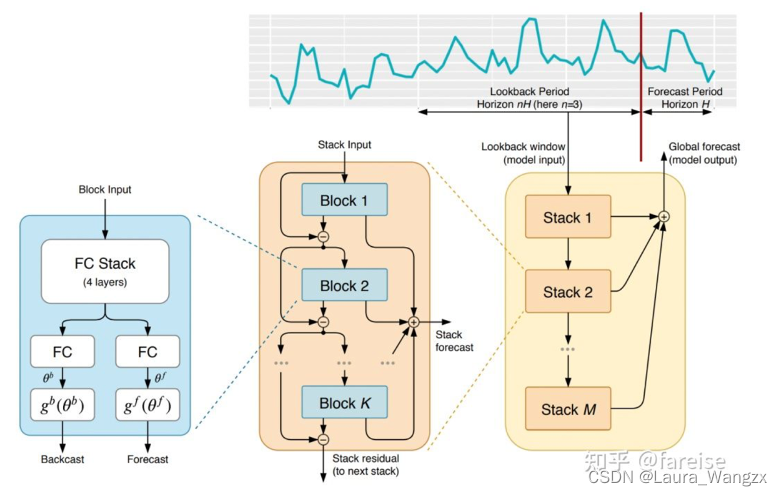
(图片来源于知乎fareise)
最终,每个block对输入的序列进行处理后,输出一个预测未来的序列,以及一个预测过去的序列。每个block的输入,是上一层block的输入减去上一层block的输出。通过这种方式,模型每层需要处理的是之前层无法正确拟合的残差,也起到了一个将时间序列进行逐层分解,每层预测时间序列一部分的作用。最终的预测结果,是各个block预测结果的加和。为了能让模型的分解具有可解释性,文中也提出了在各个层引入一些先验知识,强制让某些层学习某种类型的时间序列特性,实现可解释的时间序列分解。实现的方法是通过约束expansion coefficients到输出序列的函数形式来实现。例如想让某层block主要预测时间序列的季节性,就可以用下面的公式强制输出是季节性的。通过约束不同层学习不同信息的可视化结果,有的层学习了趋势性,有的层学习了周期性。
NbeatsX
第一版本的Nbeats,输入只能是单一的时间序列,无法输入额外的特征。而在时间序列预测问题中,诸如日期信息、节日信息、属性信息等外部特征也是非常重要的。因此,基于初版Nbeats,该团队又提出了可以引入外部特征的Nbeatsx,和初版Nbeats的主要区别是引入了外部特征X。
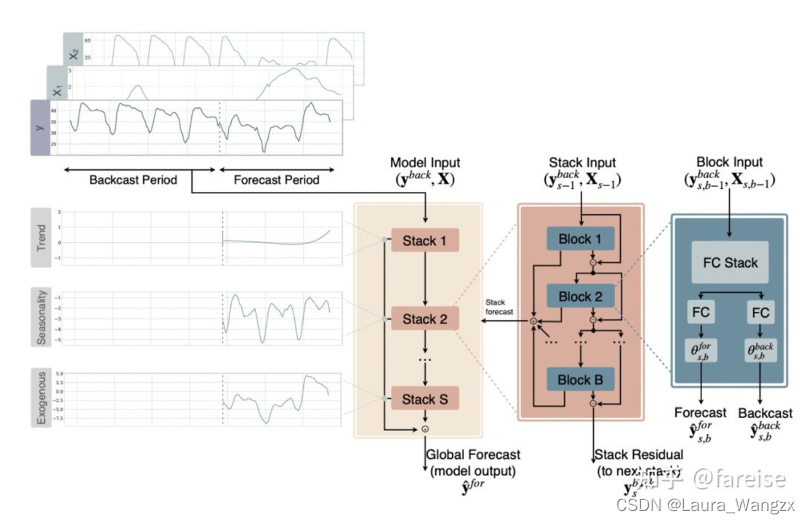
模型的主体结构和Nbeats基本一致,每个block除了输出序列外,还会输入外部特征,二者一起通过全连接层得到隐状态,再基于隐状态生成expansion coefficients。Informer
使用Transfomer实现长序列预测。针对Transfomer在长序列预测中的不足(平方时间复杂度、高内存占用和现有编解码结构的局限性),提出ProbSparse注意力机制、自注意力蒸馏技术和生成式解码器等模块解决或缓解上述问题。
- 研究意义:
(1)首先,LSTF(Long Sequence Time-Series Forecasting)长序列预测任务具有重要研究意义,对政策计划和投资避险等多种需要长时预测的任务至关重要;
(2)目前现有方法多专注于短期预测,模型缺乏长期预测能力;
(3)Transformer具有较强捕获长距离依赖的能力,但是,在计算时间复杂度和空间复杂度以及如何加强长序列输入和输出关联上都需要优化;
参考:
- 借鉴:时间序列分析预测实战之ARIMA模型:https://zhuanlan.zhihu.com/p/486586140
- 借鉴:Facebook 时间序列预测算法 Prophet:https://zhuanlan.zhihu.com/p/52330017
- 借鉴:Nbeats系列模型详解:Nbeats、NbeatsX、GAGA :
https://zhuanlan.zhihu.com/p/524324895 - 借鉴:基于Transformer的时间序列预测-Informer-AAAI21 BEST PAPER:https://zhuanlan.zhihu.com/p/353228710
- 趋势项模型 :
-
相关阅读:
Java编程常见问题汇总六
分块查找 确定查找位置
疫苗预约系统,疫苗接种管理系统,疫苗预约管理系统毕设作品
Vue error:0308010C:digital envelope routines::unsupported
【RocketMQ】RocketMQ存储结构设计
学网络安全可以参考什么方向?该怎么学?
Mysql热备增量备份与恢复(-)--备份部分
安卓手机安装Linux然后在其中安装(jdk,MySQL,git)
【ModelSim】查看波形图(Wave)和数据流图(DataFlow),以4-bit计数器为例
python爬虫获取豆瓣前top250的标题(简单)
- 原文地址:https://blog.csdn.net/qq_37486501/article/details/127647116