NC49 最长的括号子串

描述
给出一个长度为 n 的，仅包含字符 ‘(’ 和 ‘)’ 的字符串，计算最长的格式正确的括号子串的长度。

例1: 对于字符串 “(()” 来说，最长的格式正确的子串是 “()” ，长度为 2 .
例2：对于字符串 “)()())” , 来说, 最长的格式正确的子串是 “()()” ，长度为 4 .

字符串长度：0≤n≤ 5*10^5

要求时间复杂度 O(n) ,空间复杂度 O(n).

示例1
输入："(()"
返回值：2

示例2
输入："(())"
返回值：4
1
2
3
4
5
6
7

牛客网
思路：只有左括号有时，才会有合适的右括号，因此左括号的下标入栈。
当栈不为空弹出值，并减去对应括号的下一个坐标值（右括号与左括号对应上），如果为空，说明右括号已经没有其对应的左括号了，与start相减，start用来保存已经匹配完的左括号的下标位置。

import java.util.*;
public class Solution {
    public int longestValidParentheses (String s) {
        int res = 0;
        //记录上一次连续括号结束的位置
        int start = -1; 
        Stack<Integer> st = new Stack<Integer>();
        for(int i = 0; i < s.length(); i++){
            //左括号入栈
            if(s.charAt(i) == '(') 
                st.push(i);
            //右括号
            else{ 
                //如果右括号时栈为空，不合法，设置为结束位置
                if(st.isEmpty()) 
                    start = i;
                else{
                    //弹出左括号
                    st.pop(); 
                    //栈中还有左括号，说明右括号不够，减去栈顶位置就是长度
                    if(!st.empty()) 
                        res = Math.max(res, i - st.peek());
                    //栈中没有括号，说明左右括号行号，减去上一次结束的位置就是长度
                    else 
                        res = Math.max(res, i - start);
                }
            }
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

动态规划：
动态规划算法的基本思想是：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。

思路：
像这种子串长度的题，一般都涉及状态转移，可以用动态规划的方式。

• step 1：用dp[i]表示以下标为i的字符为结束点的最长合法括号长度
• step 2：很明显知道左括号不能做结尾，因此但是左括号都是dp[i]=0。
• step 3：我们遍历字符串，因为第一位不管是左括号还是右括号dp数组都是0，因此跳过，后续只查看右括号的情况，右括号有两种情况：
  
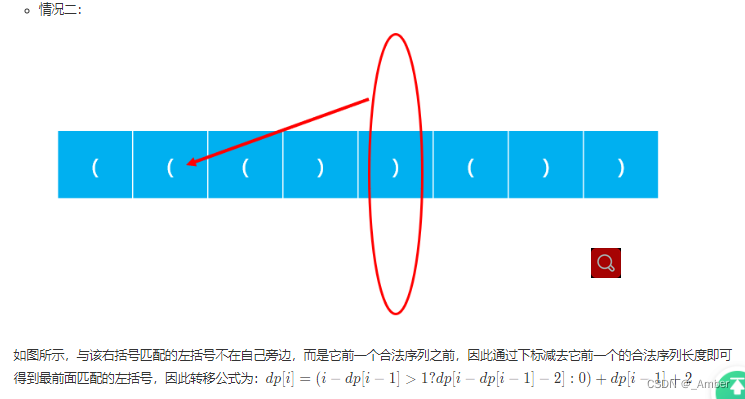
• step 4：每次检查完维护最大值即可。

import java.util.*;
public class Solution {
    public int longestValidParentheses (String s) {
        int res = 0;
        //长度为0的串或者空串，返回0
        if(s.length() == 0 || s == null) 
            return res;
        //dp[i]表示以下标为i的字符为结束点的最长合法括号长度
        int[] dp = new int[s.length()];  
        //第一位不管是左括号还是右括号都是0，因此不用管
        for(int i = 1; i < s.length(); i++){ 
            //取到左括号记为0，有右括号才合法
            if(s.charAt(i) == ')'){ 
                //如果该右括号前一位就是左括号
                if(s.charAt(i - 1) == '(') 
                    //计数+
                    dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2; 
                //找到这一段连续合法括号序列前第一个左括号做匹配
                else if(i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') 
                    dp[i] = (i - dp[i - 1] > 1 ? dp[i - dp[i - 1] - 2] : 0) + dp[i - 1] + 2;
            }
            //维护最大值
            res = Math.max(res, dp[i]); 
        }
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28