leetcode 算法-二叉树java总结——正在更新

系列文章目录

---

---

前言

提前要了解二叉树的分类 二叉树的两种存储方式 二叉树的两大种遍历方式以及深度遍历中的三种遍历方式 常常与dfs bfs混合使用
本文只介绍二叉树相关的leetcode习题 对基础的语法知识点不做过多赘述

采用Carl哥的图片来作为汇总图

二叉树遍历

1、leetcode 144. 二叉树的前序遍历

递归法 O（n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> ans = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        dfs(root);
        return ans;
    }
    public void dfs(TreeNode root){
        if(root == null) return;
        ans.add(root.val);
         dfs(root.left);
        dfs(root.right);

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

迭代法O(n)

class Solution {
    List<Integer> ans = new ArrayList<>();
    Stack<TreeNode> st = new Stack<>();
    public List<Integer> preorderTraversal(TreeNode root) {
         TreeNode cur = root;
         while(cur != null || !st.isEmpty()){
             while(cur != null){
                ans.add(cur.val);
                 st.push(cur);
                 cur = cur.left;
             }
             cur = st.pop();           
             cur = cur.right;
         }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2、 145. 二叉树的后序遍历

先遍历根右左 然后翻转过来

class Solution {
     List<Integer> ans = new ArrayList<>();
     Stack<TreeNode> st = new Stack<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        TreeNode cur = root;
        while(cur != null || !st.isEmpty()){
            while(cur != null){
                ans.add(cur.val);
                st.push(cur);
                cur = cur.right;
            }
            cur = st.pop();
            cur = cur.left;           
        }
        Collections.reverse(ans);
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

建立一个上一个节点

class Solution {
     List<Integer> ans = new ArrayList<>();
     Stack<TreeNode> st = new Stack<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        TreeNode cur = root;
        TreeNode pre = null;
        while(cur != null || !st.isEmpty()){
            while(cur != null){              
                st.push(cur);
                cur = cur.left;
            }
            cur = st.peek();
            //右边表示没遍历上一个节点
            if(cur.right != null && cur.right != pre){
                cur = cur.right;
            }else{
                st.pop();
                ans.add(cur.val);
                pre = cur;
                cur = null;   
            }
                    
        }
        
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

---

3、leetcode 94. 二叉树的中序遍历-java版本

二叉树的层序遍历

4、leetcode 102. 二叉树的层序遍历-java实现

5、107. 二叉树的层序遍历 II-java实现

6、199. 二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

层序遍历的模板 在每一层中把该层中最后一个元素放入队列中即可

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
         List<Integer> ans = new ArrayList<>();
        if(root == null) return ans;
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.add(root);
        while(!q.isEmpty()){
            int len = q.size();
            for(int i = 0 ; i < len ; i++){
                TreeNode t = q.poll();
                if(t.left != null)  q.add(t.left);
                if(t.right != null) q.add(t.right);
                if(i == len-1) ans.add(t.val);
            }
             
        }
        return ans;
 
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

7、637. 二叉树的层平均值

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> ans = new ArrayList<>();
        Queue<TreeNode> q = new LinkedList<>();
        if(root == null) return ans;
        q.add(root);
        while(!q.isEmpty()){
            int len = q.size();
            double sum = 0 ;
            for(int i = 0 ; i < len ; i ++){
                TreeNode t  = q.poll();
                sum += t.val;
                if(t.left != null) q.add(t.left);
                if(t.right != null) q.add(t.right);
            }
            ans.add(sum/len);
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

8、429. N 叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

/*
// Definition for a Node.
class Node {
    public int val;
    public List children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> ans = new ArrayList<>();        
        Queue<Node> q = new LinkedList<>();
        if(root == null) return ans;
        q.add(root);
        while(!q.isEmpty()){
            List<Integer> res = new ArrayList<>();
            int len = q.size();
            for(int i = 0 ; i < len ; i ++){
                Node t = q.poll();
                res.add(t.val);
                 for(Node c : t.children) q.add(c);
            }
            ans.add(res);
        }
        return ans ;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

9、515. 在每个树行中找最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Queue<TreeNode> q = new LinkedList<>();
        if(root == null) return ans;
        q.add(root);
        while(!q.isEmpty()){
            int len = q.size();
            int m = Integer.MIN_VALUE ;
            for(int i = 0 ; i < len ; i++){
                TreeNode t = q.poll();
                  m = Math.max(m,t.val);
                if(t.left != null) q.add(t.left);
                if(t.right != null) q.add(t.right);             
            }
             ans.add(m);
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

10、leetcode 116. 填充每个节点的下一个右侧节点指针-java实现

11、117. 填充每个节点的下一个右侧节点指针 II

二叉树的深度

12、leetcode 104. 二叉树的最大深度-java实现

13、leetcode 111. 二叉树的最小深度-java实现

14、 226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) return root;
        TreeNode t = root.left;
        root.left = root.right;
        root.right = t ;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

15、leetcode 101. 对称二叉树-java实现

16、222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

输入：root = [1,2,3,4,5,6]
输出：6

用二分的思想 O(log^2 n)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0 ;
        int x = 1 , y = 1 ;
        TreeNode l = root.left ;
        TreeNode r = root.right ;
        while(l != null){//如果是root 的话 那么x y 初始化要是0
            l = l.left ;
            x++;
        } 
        while(r  != null){
            r = r.right;
            y++;
        } 
        //二者相同为满二叉树 2^x -1 
        if(x == y) return (1 << x) -1;
        //递归到左边算加上根节点 在递归到右边算
        return countNodes(root.left) + 1 + countNodes(root.right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

17、leetcode 110. 平衡二叉树-java实现

18、257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

输入：root = [1,2,3,null,5]
输出：[“1->2->5”,“1->3”]

时间复杂度 O(n)
1、从根结点出发，递归走所有的路径，并把路径的值记录下来
2、递归过程中
若左子树和右子树都为null，则返回记录的路径s
若左子树不为null，则把左子树的值加入到路径中，递归到左子树
若右子树不为null，则把右子树的值加入到路径中，递归到右子树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<String> ans = new ArrayList<>();
    public List<String> binaryTreePaths(TreeNode root) {
        if(root == null) return ans ;
        dfs(root,""+root.val);
        return ans;
    }
    public void dfs(TreeNode root,String s){
        if(root.left ==null && root.right ==null){
            ans.add(s);
            return ;
        }       
        if(root.left != null) dfs(root.left,s + "->"+root.left.val);
        if(root.right != null) dfs(root.right,s + "->"+root.right.val);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

19、 04. 左叶子之和

原文链接
给定二叉树的根节点 root ，返回所有左叶子之和。

输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int sum = 0 ;
    public int sumOfLeftLeaves(TreeNode root) {
         if (root == null) return 0;
        
        if(root.left != null){//判断是否是左节点
            if(root.left.left == null && root.left.right == null){//判断是叶子节点
                sum += root.left.val;
            }
        }
        sumOfLeftLeaves(root.left);
        sumOfLeftLeaves(root.right);
        return sum ;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

20 、 513. 找树左下角的值

原题
给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

输入: root = [2,1,3]
输出: 1

dfs加一个最大深度 每次更新它
如果层序遍历的话 加一个i=0的判断就可以遍历到最后一层的第一个点了

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int t = 0 , maxh ;
    public int findBottomLeftValue(TreeNode root) {
        dfs(root,1);//加一个深度
        return t ;
    }
    public void dfs(TreeNode root,int h){
        if(root == null) return ;
        if(h > maxh){//更新最大深度 终止条件
            maxh = h ;
            t = root.val;
        }
         dfs(root.left , h+1);
         dfs(root.right,h+1);

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

21、leetcode 112. 路径总和-java实现

22、leetcode 113. 路径总和 II-java实现

23、leetcode 105. 从前序与中序遍历序列构造二叉树-java实现

24、leetcode 106. 从中序与后序遍历序列构造二叉树-java实现

25、654. 最大二叉树

原文

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
- 空数组，无子节点。
- [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
- 空数组，无子节点。
- 只有一个元素，所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
- 只有一个元素，所以子节点是一个值为 0 的节点。
- 空数组，无子节点。
以树上任意一点x为根构成的子树中，

1. 各节点的pos是连续的，且对pos的中序遍历即为原序列顺序（由pos满足二叉查找树可得）

2. x点的val为全子树最小（由val满足堆可得） 这道题是最大

这是n^2级别

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
       return dfs(nums,0,nums.length-1);
    }
    public TreeNode dfs(int[] nums , int l , int r){
        if(l > r ) return null;
        int root = l ;
         for(int i = l+1 ; i <= r ; i++){
              if(nums[root] < nums[i] ) root = i ;   
         }      
        TreeNode res = new TreeNode(nums[root]);
        res.left = dfs(nums,l ,root-1);
        res.right = dfs(nums,root+1 , r );
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

单调栈做法O(n)

完整的题解参考这篇

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        Stack<TreeNode> st = new Stack<>(); 
         for(int x : nums){
             TreeNode node = new TreeNode(x);
             //找到最大值
             while(!st.isEmpty() && st.peek().val < x ){
                 //将小于最大值的那个节点的左儿子
                 node.left = st.peek() ;
                 st.pop();
             }
             if(!st.empty()) st.peek().right = node;
             st.push(node);
         }
         while(st.size()>1) st.pop();
         return st.peek();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

26、617. 合并二叉树

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null) return root2;
        if(root2 == null) return root1;
        root1.val += root2.val;
        root1.left = mergeTrees(root1.left ,root2.left);
        root1.right = mergeTrees(root1.right , root2.right);
        return root1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

27、700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

时间复杂度就是二叉树的高度

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root == null) return root ;
        if(root.val == val) return root ;
        if(root.val > val ) return searchBST(root.left,val);
        else return  searchBST(root.right,val);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

28、leetcode 98. 验证二叉搜索树-java实现

29、leetcode 99. 恢复二叉搜索树-java实现

30、530. 二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

输入：root = [4,2,6,1,3]
输出：1

二叉搜索树中序遍历是递增的 最小值就是当前相邻两个节点之间

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int m = Integer.MAX_VALUE ;
    TreeNode pre ;//记录前一个节点
    //因为是中序遍历 二叉搜索树中 所以pre.val 一定小与root.val 这个Math.abs可以不加
    public int getMinimumDifference(TreeNode root) {    
        dfs(root);
        return m ;
    }
    public void dfs(TreeNode root){
        if(root == null) return   ;
        dfs(root.left);
         if(pre != null){
             m = Math.min(m ,  root.val - pre.val  );
           //  m = Math.min(m , Math.abs(root.val - pre.val ));
         }
         pre = root ;
         dfs(root.right);
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

31、501. 二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

输入：root = [1,null,2,2]
输出：[2]

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> res = new ArrayList<>();
    int maxCount = 0 ;
    int count = 0 ;
    TreeNode pre;
    public int[] findMode(TreeNode root) {
        dfs(root) ;
        int[] ans = new int[res.size()];
        for(int i = 0 ; i < res.size() ; i++) ans[i] = res.get(i);
         return ans ;
    }
    public void dfs(TreeNode root){
        if(root == null) return ;
        dfs(root.left);
        //第一个或者连续相等的
        if(pre == null || root.val == pre.val ) count++;
        else   count = 1 ;
         pre = root ;//更新
        if(count > maxCount){
            res = new ArrayList<>();
            res.add(root.val);
            maxCount = count;
        } else if(count == maxCount){
            res.add(root.val);
        }
       
        dfs(root.right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

32、236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

题解

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
 
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return  dfs(root , p  ,q );
    }
    public TreeNode dfs(TreeNode root , TreeNode p , TreeNode q){
         if(root == null || root == p || root == q) return root;
         TreeNode left =  dfs(root.left , p ,q );
         TreeNode right =  dfs(root.right, p , q);
         if(left != null && right != null) return root ;
         if(left != null ) return left ;
         return right ;

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null) return right;
        if(right == null) return left;
        return root;
    }
}

 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

还有一种方法是通过二进制的表示方式来保存q和p 1 0
这样子 采用的是中序遍历

235. 二叉搜索树的最近公共祖先

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
所以不用判空

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       if(root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left,p,q);
       if(root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right,p,q);
       return root ;
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if(root == null) return new TreeNode(val);
        if(root.val > val) root.left = insertIntoBST(root.left ,val);
        if(root.val < val) root.right = insertIntoBST(root.right,val);
        return root ;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。

二叉树的删除是有些麻烦的，因为要考虑节点的所处情况

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null) return null;
        if(key == root.val){
            //有左节点或右节点
            if(root.left == null) return root.right;
            if(root.right == null) return root.left; 
            //找后继节点 左右儿子都有
            TreeNode cur = root.right;
            while(cur.left !=  null) cur = cur.left;
             cur.left = root.left;
            //root.val = cur.val ;
            return root.right;//新的根节点
        }else if(key > root.val) root.right = deleteNode(root.right , key);
        else  root.left =  deleteNode(root.left , key);
        //如果是叶子节点 直接返回
        return root;
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

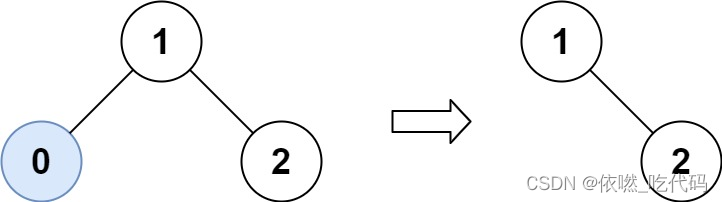
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null) return null;
        if(root.val < low) return trimBST(root.right ,low, high);
        if(root.val > high) return trimBST(root.left,low ,high);
        root.left = trimBST(root.left , low ,high);
        root.right = trimBST(root.right ,low, high);
        return root ;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

108.将有序数组转换为二叉搜索树

538.把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
//右 根 左  反中序遍历的形式就行
    int sum = 0 ;
    public TreeNode convertBST(TreeNode root) {
        dfs(root);
        return root ;
    }
    public void dfs(TreeNode root){
        if(root == null) return ;
        dfs(root.right);
        int x = root.val ;
        root.val += sum ;
        sum += x ;
        dfs(root.left);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31