前端算法之搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。这就是搜索插入位置算法。与二分算法很相似

示例 1:

输入: nums = [1,3,5,6], target = 5输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7输出: 4

 
var searchInsert = function(nums, target) {
        let left = 0,right = nums.length -1 ,n = nums.length
            while (left <= right) {
                let mid = (left + right) >> 1
            if(nums[mid] >= target) {
                    // 值在左侧
                    n = mid
                    right = mid - 1
            }else {
                // 右侧
                left = mid + 1       
            }
            }
            return n
};

解题如上。此题的解题方案如下：

1. 根据题头我们可以知道这是一个排序好的数组。所以我们直接可以基于二分查找来进行坐。

2. 我们在数组中找到目标值，返回其索引，跟之前二分查找的时候是一致的。

3. 如果目标值不存在数组中，那么返回它会被插入的位置。这里可以的理解就是，分为两种，

• 第一种，target 的值是在数组中的，这时候我们利用二分可以找到最近的下标，返回出去即可解答。
• 第二种，target的值不在数组中，也就是说数组中没有。如何进行呢？

假设数组为： [1,2,3,4,5,6]  target 为 0 ，默认抛出的值 N  为 0

这样的话，我们通过三次二分就可以发现1的坐标为0.即 我们找寻最接近的值的下标则为0.

但是如果我们的 target 为 7 呢。 这时候会发现测试用例走不过去了。

这是什么愿意呢？是因为，我们的target为7，则依旧需要三次二分。

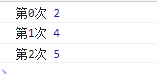
第一次二分后的中间值是2，第二次4 ，第三次5.但是它依旧没有找到位置。说明方法没进入，这时候如果初始化 N 是 0 的话，则方法会直接返回 0  造成错误。这时候大家明白了吧。

也就是说，当target 的值大于 nums[mid]的值的时候， 就证明target 比 nums 数组的当前的中间件的值大，我们只需要移动left 坐标，让二分继续即可。所以我们就默认初始化N应该是数组的长度。直到数组的某个值大于 target 的值的时候，这时候它才能被改变为当前中间值的下标。否则的话就是 数组的长度。

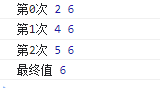
 如上。三次打印都没有进入判断方法。所以它默认返回的则是数组的长度。如果进去的话，则一定会修改n的值为当前中间值的下标。