LeetCode90. 子集 II

1 题目描述

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：
输入：nums = [0]
输出：[[],[0]]

提示：
1 <= nums.length <= 10
-10 <= nums[i] <= 10

来源：力扣（LeetCode）
链接：90. 子集 II

2 算法设计

本题属于求子集类问题，将该过程抽象为一棵树，即收集的是树的所有节点。本题的关键在于解集中不能包含重复的子集，这里需要做去重处理。 本题中去重采用used[]布尔数组，用来标识数组中的元素是否被访问过，其过程如下图所示：

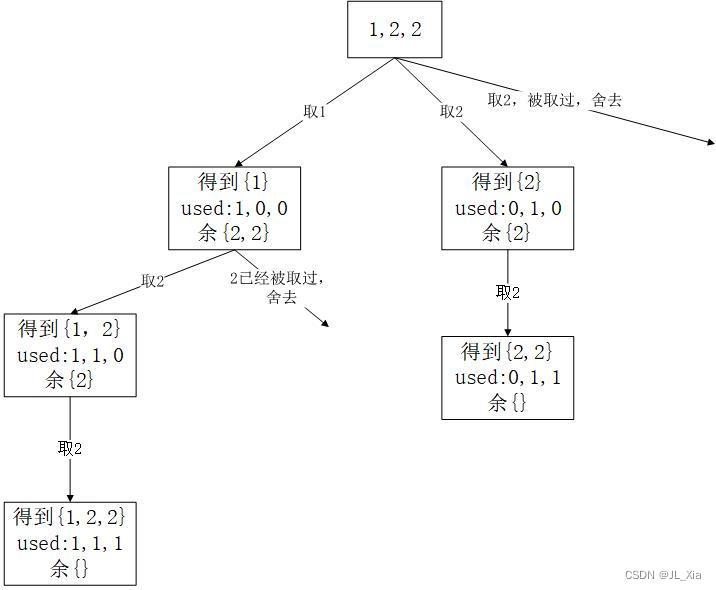
从上图可知，我们最后需要的结果就是各个节点上收集的结果集。
关于used[]布尔数组去重的说明：

• 若used[i-1]==true，则说明同一树枝nums[i-1]使用过
• 若used[i-1]==false，则说明同一层nums[i-1]使用过

3 代码实现

public class SubsetsWithDup {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    boolean[] used;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        used = new boolean[nums.length];
        Arrays.fill(used,false);
        //排序，将所有值相等的元素放在一起
        Arrays.sort(nums);
        backTracking(nums,0);

        return res;
    }
    public void backTracking(int[] nums, int startIndex){

        res.add(new ArrayList<>(path));
        if (startIndex >= nums.length){
            return;
        }

        for (int i = startIndex;i < nums.length;i++){
            //去重
            //used[i-1]==true说明同一树枝nums[i-1]使用过
            //used[i-1]==false说明同一层nums[i-1]使用过
            if (i > 0 && used[i-1]==false && nums[i-1]==nums[i]){
                continue;
            }
            path.add(nums[i]);
            used[i] = true;
            backTracking(nums,i+1);
            used[i] = false;
            path.removeLast();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

4 测试结果