80行代码轻松搞定反向传播神经网络(BPNN)

后向传播神经网络

一、原理

BP(Back Propagation)算法是通过将网络预测值与实际值做对比，不断修改权重从而尽量将他们之间的均方根误差降低到最小的算法。该算法由最后的节点向前不断传递信息，所以被称为后向传播算法。BP算法具有简单易行、计算量小和并行性强等优点，其实质是求解误差函数最小值的问题，但由于梯度下降本身的缺点，容易陷入局部最小值，且根据学习率，有可能会导致收敛速度慢，学习效率低等缺点。

整个BPNN可以划分为两个阶段：

第一阶段：前向传播阶段

这一阶段，节点之间通过权重边相互映射到新的节点中，第$i$层的节点信息由第$i-1$层映射得到，满足以下公式：
$$I_i=\sum _{i=1}^n{w}_{ij}{O}_j+{\theta }_i$$
其中，$O_j$表示上一层节点的输出信息，$w_{ij}$表示节点$j$和节点$i$的权重边，${\theta }_i$表示偏置量(Bias)。

我们通过添加一个激活函数，将原先的线性映射变为非线性映射，例如使用Sigmoid函数：
$$O_i=\frac{1}{1+e^{-I_i}}$$
第二阶段：反向传播

BP算法基于梯度下降，每次对参数的迭代都是梯度最快下降的方向，其误差值的评估为：
$$E=\frac{1}{2}\sum _{j=1}^l({\hat{y}}_j^k-y_j^k{)}^2$$
前面的0.5是为了化简求导，常数项影响不大。

对于某一权重参数$w_{hj}$，给定一个学习率$\sigma$，其变化率为对误差值(也称作损失函数)的求导：
$$△w_{hj}=\frac{\delta E}{\delta w_{hj}}$$
根据梯度下降算法，他的变化值应该是其梯度的反方向。再加上学习率做平滑，所以最后的更新量为：
$$△w_{hj}=-\sigma \frac{\delta E}{\delta w_{hj}}$$
注意Sigmoid函数的求导结果为：
$$O^{\prime }=O(1-O)$$
这里不给出具体求导步骤，感兴趣的朋友可以自己试着推一推。

于是，根据链式求导规则，在输出层单元$j$，误差$Err$的计算表达为：
$$Er{r}_j=O_j(1-O_j)(T_j-O_j)$$
$T_j$表示在这个单元上的真实结果。

根据BP原理，对于单元$j$的误差，来源于与他相关的$n$个隐含层单元映射，而对于某个隐含层映射$i$，也有可能对$k$个输出层节点产生影响(多对多关系)，所以在隐层的更新中，需要考虑所有从输出层传播回来的信息。

对于隐层节点$i$，有：
$$Er{r}_i=O_i(1-O_i)\ast \sum _{j=1}^k{w}_{ij}Er{r}_j$$
了解完误差传播的规则之后，我们就需要对参数进行更新啦！

那么每一层权重的更新可以表示为：
$$\begin{gathered} △w_{ij}=\sigma Er{r}_j{O}_i \\ {w}_{ij}=w_{ij}+△w_{ij} \end{gathered}$$
偏置的更新可以表示为：
$$\begin{gathered} △{\theta }_j=\sigma Er{r}_j \\ {\theta }_j={\theta }_j+\sigma △{\theta }_j \end{gathered}$$
BP算法迭代停止条件为：

• 前一周期所有的权重变化率都小于给定阈值
• 前一周期误差百分比小于给定阈值
• 超出给定的迭代周期数

---

二、案例

给定一个前馈神经网络如下，共有九个输入节点，可以看做九个特征维度，两个隐层节点和一个输出层节点。

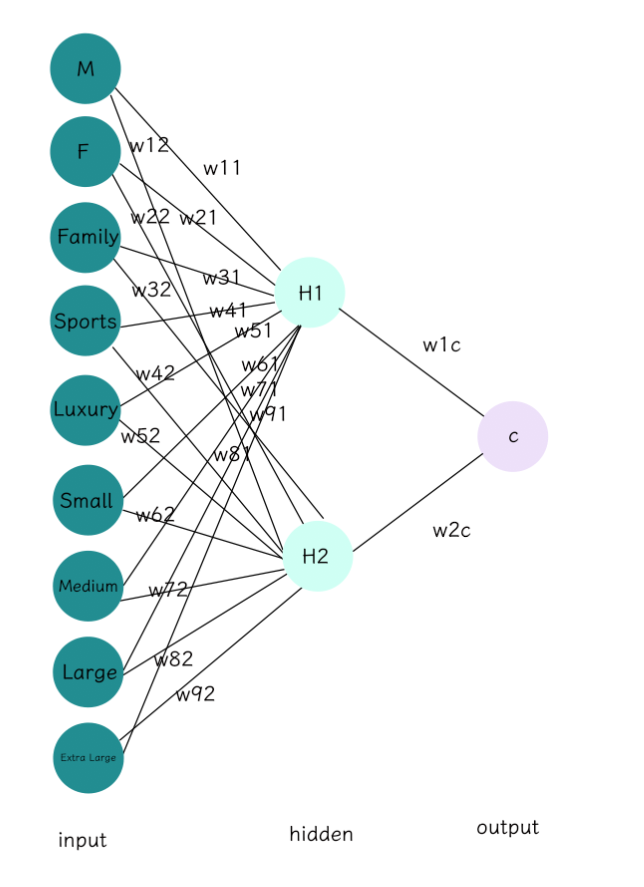
首先第一步，我们需要给定权重的初始值和学习率：

隐层

输出层

输入初始值为

1,0,1,0,0,1,0,0,0

学习率

lr=0.01

偏置

对于每个节点，净输入值表示为：
$$I=\theta +\sum _{i=1}^n{w}_i{v}_i$$
其中，$\theta$ 表示偏置量，$w_i$表示分支权重，$v_i$表示节点值。

输出值表示为：
$$O=\frac{1}{1+e^{-I}}$$
输出结果

输出层的误差值计算为
$$Err=O\ast (1-O)\ast (T-O)$$
其中，$O$表示节点输出，$T$表示真实值

隐层节点的误差计算为：
$$Err=O\ast (1-O)\ast \sum _{i=1}^{n}Er{r}_i\ast w_i$$
其中，$Err$表示从高层传过来的误差。

计算每个节点的误差

偏置量的更新方程表示为:
$${\theta }_{new}={\theta }_{old}+lr\ast (Err)$$
权重的更新方程表示为：
$$w_{new}=w_{old}+lr\ast Err\ast O$$

更新权重和偏置

这里只给出了链式求导用到的节点和权重

---

三、代码实现

1️⃣ 导入需要的库，以及我们需要用的函数

import math
import random
# step 1. 构建常用函数

# 激活函数
def sigmoid(x):
    return math.tanh(x)
def ReLU(x):
    return x if x>0 else 0
def derived_sigmiod(x):
    # (O)(1-O)(T-O)
    return x-x**2

# 生成随机数
def getRandom(a,b):
    return (b-a)*random.random()+a

# 生成一个矩阵
def makeMatrix(m,n,val=0.0):
    # 默认以0填充这个m*n的矩阵
    return [[val]*n for _ in range(m)]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

2️⃣ 初始化参数

这个阶段我们需要做的工作有：

• 初始化节点个数
• 创建权重矩阵并给定初始值
• 保存各种参数量
• 创建数据容器保存各层输出结果
• 也可以设置动量参数

# step 2. 初始化参数
# 这部分主要有：节点个数、隐层个数、输出层个数
# 可以类似于torch.nn.Linear
class BPNN:
    def __init__(self,n_in,n_out,n_hidden=10,lr=0.1,m=0.1):
        self.n_in=n_in+1 # 加一个偏置节点
        self.n_hidden=n_hidden+1 # 加一个偏置节点
        self.n_out=n_out
        self.lr=lr
        self.m=m

        # 生成链接权重
        # 这里用的是全连接，所以对应的映射就是 [节点个数A，节点个数B]
        self.weight_hidden=makeMatrix(self.n_in,self.n_hidden)
        self.weight_out=makeMatrix(self.n_hidden,self.n_out)
        # 对权重进行初始化
        for i,row in enumerate(self.weight_hidden):
            for j,val in enumerate(row):
                self.weight_hidden[i][j]=getRandom(-0.2,0.2)
        for i,row in enumerate(self.weight_out):
            for j,val in enumerate(row):
                self.weight_out[i][j]=getRandom(-0.2,0.2)

        # 存储数据的矩阵
        self.in_matrix=[1.0]*self.n_in
        self.hidden_matrix=[1.0]*self.n_hidden
        self.out_matrix=[1.0]*self.n_out

        # 设置动量矩阵
        # 保存上一次梯度下降方向
        self.ci=makeMatrix(self.n_in,self.n_hidden)
        self.co=makeMatrix(self.n_hidden,self.n_out)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

3️⃣ 正向传播

这个阶段，我们要做的有：

• 将输入数据保存到数据容器中
• 开始根据正向传播规则传播数据

  # step 3. 正向传播
    # 根据传播规则对节点值进行更新
    def update(self,inputs):
        if len(inputs)!=self.n_in-1:
            raise ValueError("Your data length is %d, but our input needs %d"%(len(inputs),self.n_in-1))
        # 设置初始值
        self.in_matrix[:-1]=inputs
        # 注意我们最后一个节点依旧是1，表示偏置节点

        # 隐层
        for i in range(self.n_hidden-1):
            accumulate=0
            for j in range(self.n_in-1):
                accumulate+=self.in_matrix[j]*self.weight_hidden[j][i]
            self.hidden_matrix[i]=sigmoid(accumulate)

        # 输出层
        for i in range(self.n_out):
            accumulate = 0
            for j in range(self.n_hidden - 1):
                accumulate += self.hidden_matrix[j] * self.weight_out[j][i]
            self.out_matrix[i] = sigmoid(accumulate)

        return self.out_matrix[:] # 返回一个副本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

4️⃣ 反向传播

这一阶段，我们要做的工作有：

• 反向计算误差
• 反向更新参数量

    # step 4. 误差反向传播
    def backpropagate(self,target):
        if len(target) != self.n_out :
            raise ValueError("Your data length is %d, but our input needs %d" % (len(target), self.n_out))
        # 计算输出层的误差
        # 根据公式： Err=O(1-O)(T-O)=(O-O**2)(True-O)
        out_err=[derived_sigmiod(o:=self.out_matrix[i])*(t-o) for i,t in enumerate(target)]
        # 计算隐层的误差
        # 根据公式：Err=(O-O**2)Sum(Err*W)
        hidden_err=[0.0]*self.n_hidden
        for i in range(self.n_hidden):
            err_tot=0.0
            for j in range(self.n_out):
                err_tot+=out_err[j]*self.weight_out[i][j]

            hidden_err[i]=derived_sigmiod(self.hidden_matrix[i])*err_tot

        # 更新权重
        # 输出层：
        # w=bias+lr*O*Err+m*(w(n-1))
        # m表示动量因子，w(n-1)是上一次的梯度下降方向
        for i in range(self.n_hidden):
            for j in range(self.n_out):
                # 更新变化量 change=O*Err
                change=self.hidden_matrix[i]*out_err[j]
                self.weight_out[i][j]+=self.lr*change+self.m*self.co[i][j]
                # 更新上一次的梯度
                self.co[i][j]=change

        # 隐含层
        for i in range(self.n_in):
            for j in range(self.n_hidden):
                change=hidden_err[j]*self.in_matrix[i]
                self.weight_hidden[i][j]+=self.lr*change+self.m*self.ci[i][j]
                self.ci[i][j]=change

        # 计算总误差
        err=0.0
        for i,v in enumerate(target):
            err+=(v-self.out_matrix[i])**2
        err/=len(target)
        return math.sqrt(err)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

总的代码为：

import math
import random

def sigmoid(x):
    return math.tanh(x)
def ReLU(x):
    return x if x>0 else 0
def derived_sigmiod(x):
    return x-x**2
def getRandom(a,b):
    return (b-a)*random.random()+a
def makeMatrix(m,n,val=0.0):
    return [[val]*n for _ in range(m)]

class BPNN:
    def __init__(self,n_in,n_out,n_hidden=10,lr=0.1,m=0.1):
        self.n_in=n_in+1 
        self.n_hidden=n_hidden+1 
        self.n_out=n_out
        self.lr=lr
        self.m=m
    	self.weight_hidden=makeMatrix(self.n_in,self.n_hidden)
    	self.weight_out=makeMatrix(self.n_hidden,self.n_out)
        
        for i,row in enumerate(self.weight_hidden):
            for j,val in enumerate(row):
                self.weight_hidden[i][j]=getRandom(-0.2,0.2)
                
        for i,row in enumerate(self.weight_out):
            for j,val in enumerate(row):
                self.weight_out[i][j]=getRandom(-0.2,0.2)
                
        self.in_matrix=[1.0]*self.n_in
        self.hidden_matrix=[1.0]*self.n_hidden
        self.out_matrix=[1.0]*self.n_out
        
        self.ci=makeMatrix(self.n_in,self.n_hidden)
        self.co=makeMatrix(self.n_hidden,self.n_out)

    def update(self,inputs):
      
        self.in_matrix[:-1]=inputs
        
        for i in range(self.n_hidden-1):
            accumulate=0
            for j in range(self.n_in-1):
                accumulate+=self.in_matrix[j]*self.weight_hidden[j][i]
            self.hidden_matrix[i]=sigmoid(accumulate)
            
        for i in range(self.n_out):
            accumulate = 0
            for j in range(self.n_hidden - 1):
                accumulate += self.hidden_matrix[j] * self.weight_out[j][i]
            self.out_matrix[i] = sigmoid(accumulate)
        return self.out_matrix[:]

    def backpropagate(self,target):
      
        out_err=[derived_sigmiod(o:=self.out_matrix[i])*(t-o) for i,t in enumerate(target)]
        
        hidden_err=[derived_sigmiod(self.hidden_matrix[i])*sum(out_err[j]*self.weight_out[i][j] for j in range(self.n_out)) for i in range(self.n_hidden) ]
        
        for i in range(self.n_hidden):
            for j in range(self.n_out):
                change=self.hidden_matrix[i]*out_err[j]
                self.weight_out[i][j]+=self.lr*change+self.m*self.co[i][j]
                self.co[i][j]=change
                
        for i in range(self.n_in):
            for j in range(self.n_hidden):
                change=hidden_err[j]*self.in_matrix[i]
                self.weight_hidden[i][j]+=self.lr*change+self.m*self.ci[i][j]
                self.ci[i][j]=change
                
        err=0.0
        for i,v in enumerate(target):
            err+=(v-self.out_matrix[i])**2
        err/=len(target)
        return math.sqrt(err)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

5️⃣ 模型使用

在这阶段我们新加两个API，用于网络训练和拟合

    def train(self,data,epochs=1000):
        best_err=1e10
        for i in range(epochs):
            err=0.0
            for j in data:
                x=j[0]
                y=j[1]

                self.update(x)
                err+=self.backpropagate(y)
            if err<best_err:
                best_err=err
        print(best_err)

    def fit(self,x):
        return [self.update(i) for i in x]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

我们也可以创建一个随机数据生成器用来获取随机数据

def getData(m,n,c=None):
    # 随机生成一组大小为m*n,类别为c的数据
    if c!=None:
        data=[[[random.uniform(0.0,2.0)]*n,[random.randint(0,c)]] for i in range(m)]
    else:
        data=[[random.uniform(0.0,2.0)]*n for _ in range(m)]
    return data
d_train=getData(20,5,1)
d_test=getData(10,5)
1
2
3
4
5
6
7
8
9

不过我们这里使用固定的模式进行测试：

# 固定模式
d=[
    [[1,0,1,0,1],[1]],
    [[1,0,1,0,1],[1]],
    [[1,0,1,0,1],[1]],
    [[1,0,1,1,1],[0]],
    [[1,0,1,0,1],[1]],
    [[1,0,1,1,1],[0]],
]
c=[
    [1,0,1,0,1],
    [1,0,1,0,1],
    [1,0,1,1,1],
    [1,0,1,0,1],
    [1,0,1,1,1],
    [1,0,1,0,1],
    [1,0,1,0,1],
    [1,0,1,1,1],
    [1,0,1,0,1],
    [1,1,1,0,1],
]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

输入数据是一个6*5大小的数据，label是一个一维数据，所以我们需要创建一个输入维度为5，输出维度为1的BPNN：

net=BPNN(5,1)

net.train(d)
print(net.fit(c))
1
2
3
4

得到的结果为：

[[0.9831619856205059], [0.9831619856205059], [0.023029882403248512], [0.9831619856205059], [0.023029882403248512], [0.9831619856205059], [0.9831619856205059], [0.02302988]]
1

可以发现确实简单实现了二分类。

当然我们也可以设定输出维度为2，结果表示为：

net=BPNN(5,2)

net.train(d)
print(["cat" if i[0]>i[1] else 'dog' for i in net.fit(c)])
1
2
3
4

Err: 0.10754377610345334
result:
['cat', 'cat', 'dog', 'cat', 'dog', 'cat', 'cat', 'dog', 'cat', 'cat']
1
2
3