2021年数维杯数学建模C题运动会优化比赛模式探索求解全过程文档及程序

2021年数维杯数学建模

C题 运动会优化比赛模式探索

原题再现：

  5月中旬恰好是各个大学召开每年一届的运动的时间节点。运动会已成为了大学校园里一道亮丽的风景线，运动会上振奋人心的开幕式、拍手称赞的比赛、激动人心的颁奖仪式都给参加运动会的同学们带来了一次精神上的享受。每一次运动会举办的过程中运动场上运动员奋勇拼搏，用自己的努力证明自己，展示自己的速度与激情。运动场下各班级啦啦队为选手们加油呐喊，展现着青春活力，运动会依然成为了校园里不可或缺的一部分。
  运动会不仅是同学们展示自己的舞台，更为重要的这是难得的提高大学生团队意识与身体素质的良机。然而，不同学院人数与性别之间的显著性差异，导致了部分学院排名的多年垄断。这也导致了大量学院运动会参与热情的下降，从而未能发挥运动会应有的作用。为此，引进一种科学而合理的运动会优化比赛模式迫在眉睫。
  已知某校运动会的积分规则为：第一名得9分，第二名至第八名获得7至1分。各学院男生和女生累积得分最终构成团体得分。附件1中给出了某大学20个学院，104个专业，共计28523名学生的分布情况数据，请结合此数据努力完成如下任务：
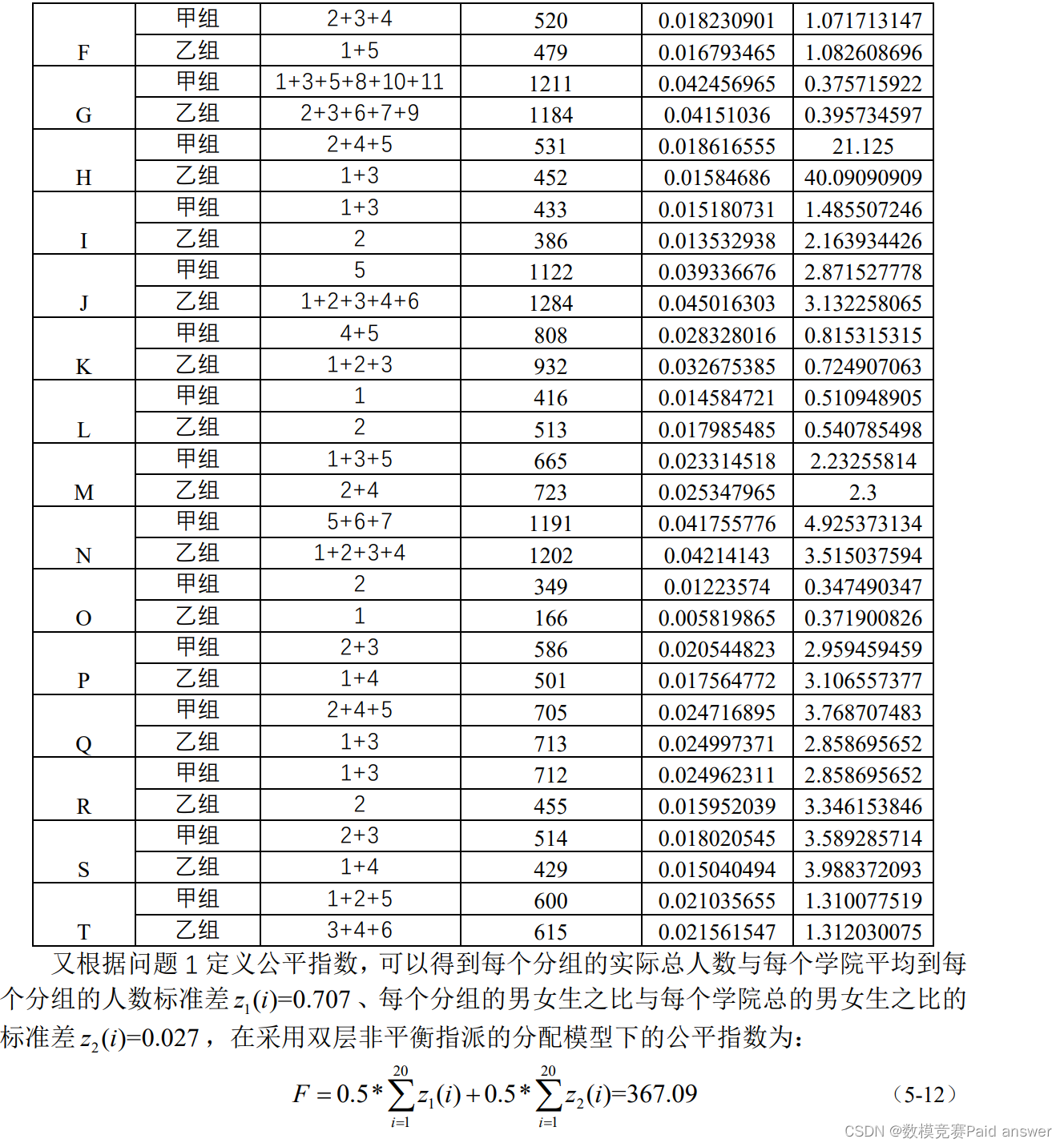
  问题1：若在比赛中允许学院合并后共同参加比赛，请你提出一个分组数量不低于12个的、各组人员总数和男女性别比较为均衡的优化分配模型，并讨论分组方案的公平指数；
  问题2：若对各个学院进行甲组和乙组分类进行比赛，请你提出最优的甲乙分组方案，并讨论这一分组方案的公平指数；
  问题3：如果特长生可以跨学院参加比赛，请你提出尽量保障各学院比赛实力更为均衡的方案。如果特长生不参加比赛您能否提出一个对各学院相对公平的加权积分方案？
  问题4：您能否通过计算机仿真模拟或理论推导来证明上述四种优化比赛模式哪个更好?

整体求解过程概述(摘要)

  为了引进一种科学而合理的运动会优化比赛模式，本文利用基于动态规划的多个数学模型，对一场学院运动会的比赛模式进行优化研究。
  针对问题 1，为了满足比赛中允许学院合并后共同参加比赛，分组数量不低于 12个的、各组人员总数和男女性别比较为均衡，建立了一个基于动态规划中的非平衡指派问题的数学模型，以各组人数及男女比例均衡为目标函数，利用匈牙利算法结合 lingo软件进行最优分配方案的求解，并定义了一种讨论比赛公平性的公平指标，从而对得到的优化分配方案进行了讨论。
  针对问题 2，为了将每个学院分为甲乙两组进行比赛，为了使得各学院的实力较均衡，通过分析考虑将每个学院按专业进行分组，再利用问题 1 建立的非平衡指派的优化分配模型求解每个学院的最优分组方案，最终确定了最优的甲乙组分配方案。
  针对问题 3，为了使各学院比赛实力更为均衡，考虑以各学院总人数近似相等为均衡条件，将特长生分配到不同的学院。因特长生与普通学生在体育竞技上的显著差异，采取将每名特长生与普通学生按 1:5 的比例进行分配。特长生分配方案类似与动态规划中的资源分配问题，因此建立动态规划中的资料分配问题模型来进行特长生分配。在考虑特长生不参加比赛的情况下，为了让各学院的实力均衡，分别给每个学院引入一个获奖概率权重，然后利用建立的公平席位分配模型，通过调节每个学院的获奖概率权重，从而使得各学院获奖的机会是均等的。
  针对问题 4，在前面 3 个问题建立的模型的基础上，拟通过计算机模拟的方式，对四种优化分配模型进行探索，并分析四种不同的公平指数，从而选择一种最优的分配模式。

问题分析：

  问题一属于数学优化问题，对于解决此类问题，我们要重点分析三个重要点，以此来建立模型。1、分组的数量为十二个；2、分好的各组人员总数要大约一致;3、各组人员中的男女比例要近似相等。由于以上原因，我们可以首先建立一个统计表的数学模型 I，再建立一个指派模型(0-1 规划的特例)的数学模型 II,然后将这 12 个组里面，每组的人数与总人数的平均值的标准差 Z1、每组的男女比例、总人数的男女比例的标准差 Z2 作为目标函数，最后求得解，找出分组方案的公平指数。
  问题二属于数学优化问题，对于解决此类问题，将每个学院分为甲组和已组,我们要重点分析两个重要点，以此来建立模型。1.按专业分组;2.将每个学院的人数按照各组人员总数和男女性别较为均衡的要来进行。由于以上原因，我们首先可以利用问题 1 建立的非平衡指派的优化分配模型对按专业分组的每个学院进行分组求解,其次讨论该分组方式的公平指数,最终确定最优的甲乙组分配方案。
  问题三属于资源分配数学问题，此类问题可以是多阶段决策过程，也可以是静态规划问题,而对于解决此类问题，都能构造动态规划模型求解。由于以上原因,我们首先可以利用附件 1 中给出的各学院人数加上按比例分配后的特长生人数与学校平均到每个学院的人数的标准差最小作为目标函数，其次求解出特长生最优分配方案，最后再利用问题 1 定义的公平指数定义讨论其公平指数。
  问题 4 属于验证问题。在前面 3 个问题建立的模型的基础上，拟通过计算机模拟的方式，对四种优化分配模型进行探索，并分析四种不同的公平指数，从而选择一种最优的分配模式。

模型的建立与求解

  从运筹学中，我们知道工作中常遇到这样的问题：有m项任务需要n个人来承担，每个人都能完成其中的每项任务，只是由于每个人的特点与专长不同，每个人完成各项任务所需的时间、费用或所产生的效益各不相同，又因为任务性质的要求和管理上的需要等原因，每项任务只能由一个人来完成，每个人也只能承担其中的一项任务.问应指派哪个人去完成哪项任务才能使完成各项任务花费的总时间最短或总费用最少，或所产生的总效益最佳.我们把这类最优匹配问题称为指派问题.
  在实际应用中指派问题通常有平衡与非平衡两种类型，即有n项任务，指派n个人员来分派完成称为平衡指派问题；有m项任务，指派n个人员来分派完成称为非平衡指派问题。根据题目条件允许 20 各学院合并为 12 个以上分组，要求建立一个分配模型使得各组人数及男女性别比例均衡。所以问题1采用以非平衡指派问题建立优化分配模型。

建立双目标非平衡指派的优化分配模型

基于匈牙利算法的模型求解

  针对此类多旅行商问题的求解过程是相当复杂的，被认为是 NP 问题。而选择算法也是相对困难的。本文选择用匈牙利算法来求解该指派问题的最优解。
  1.匈牙利算法的基本原理

  2.匈牙利算法的解题步骤


  结果：
  1.构建效率矩阵


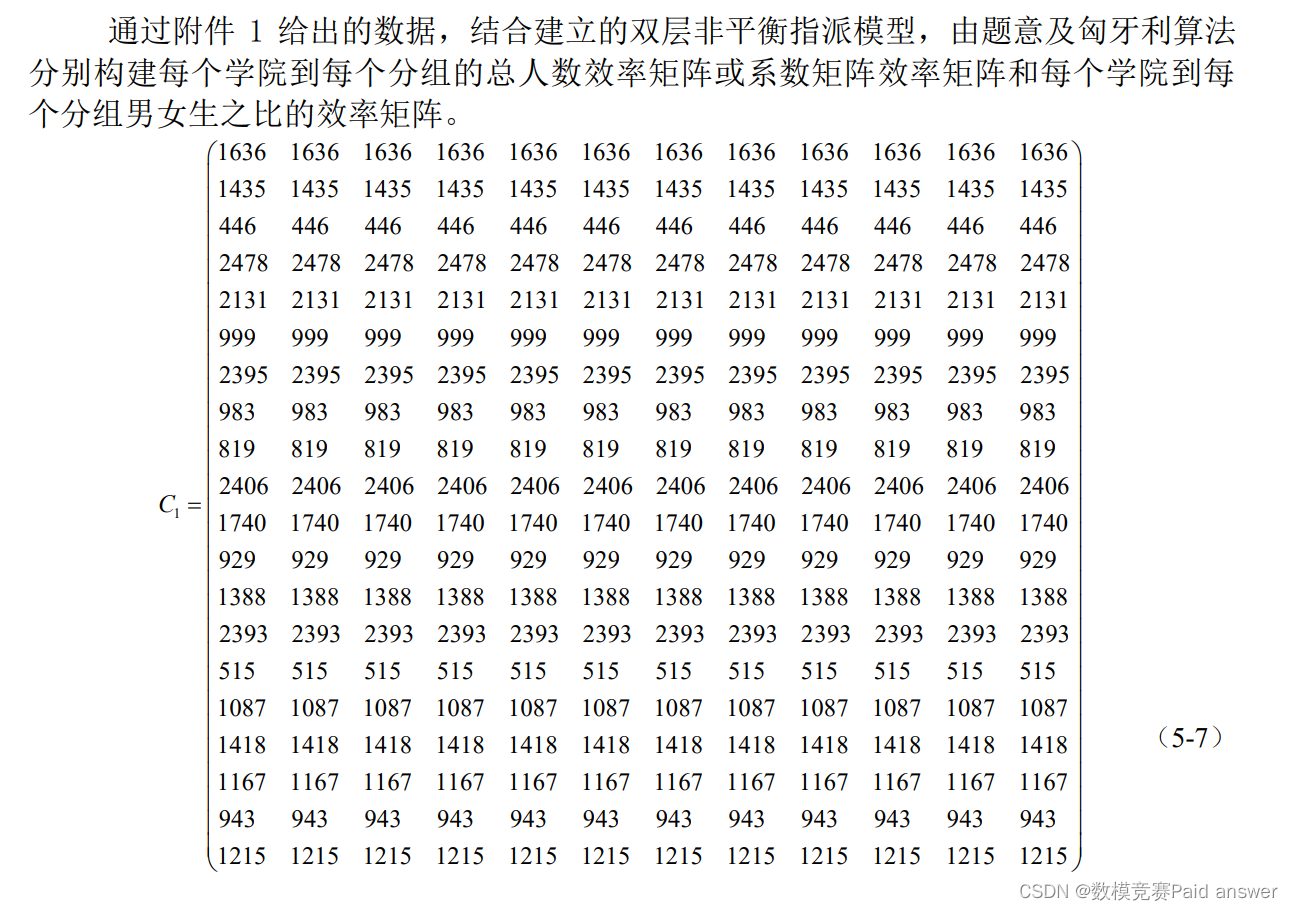
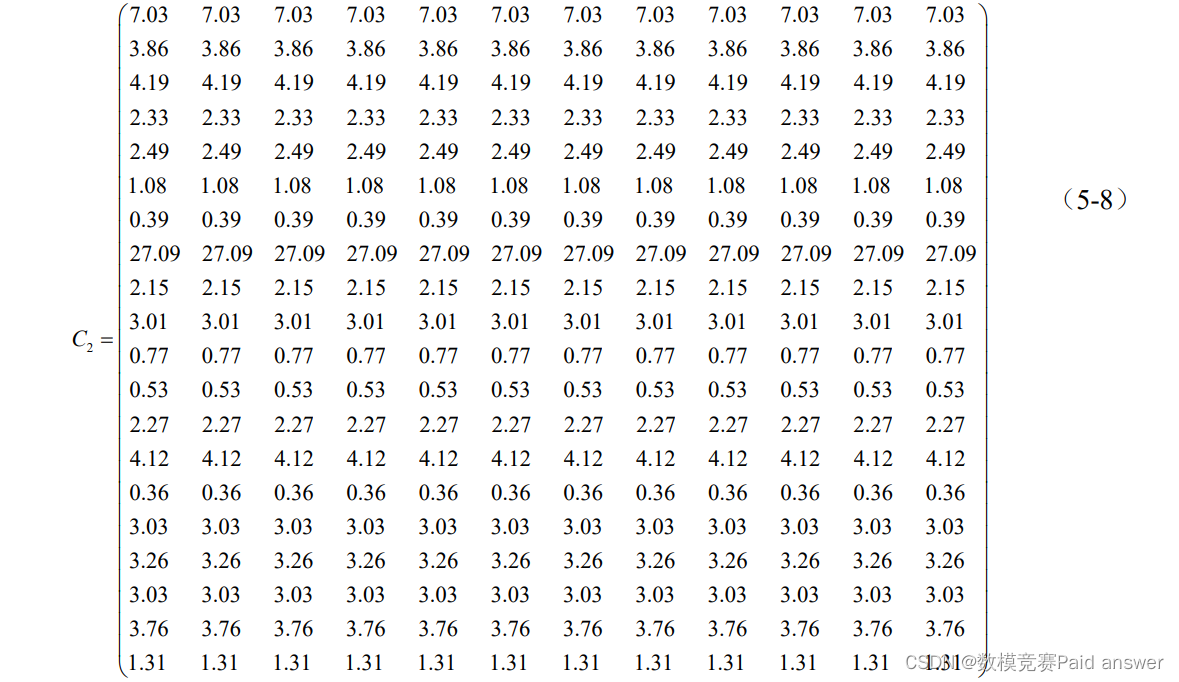
  2.模型求解

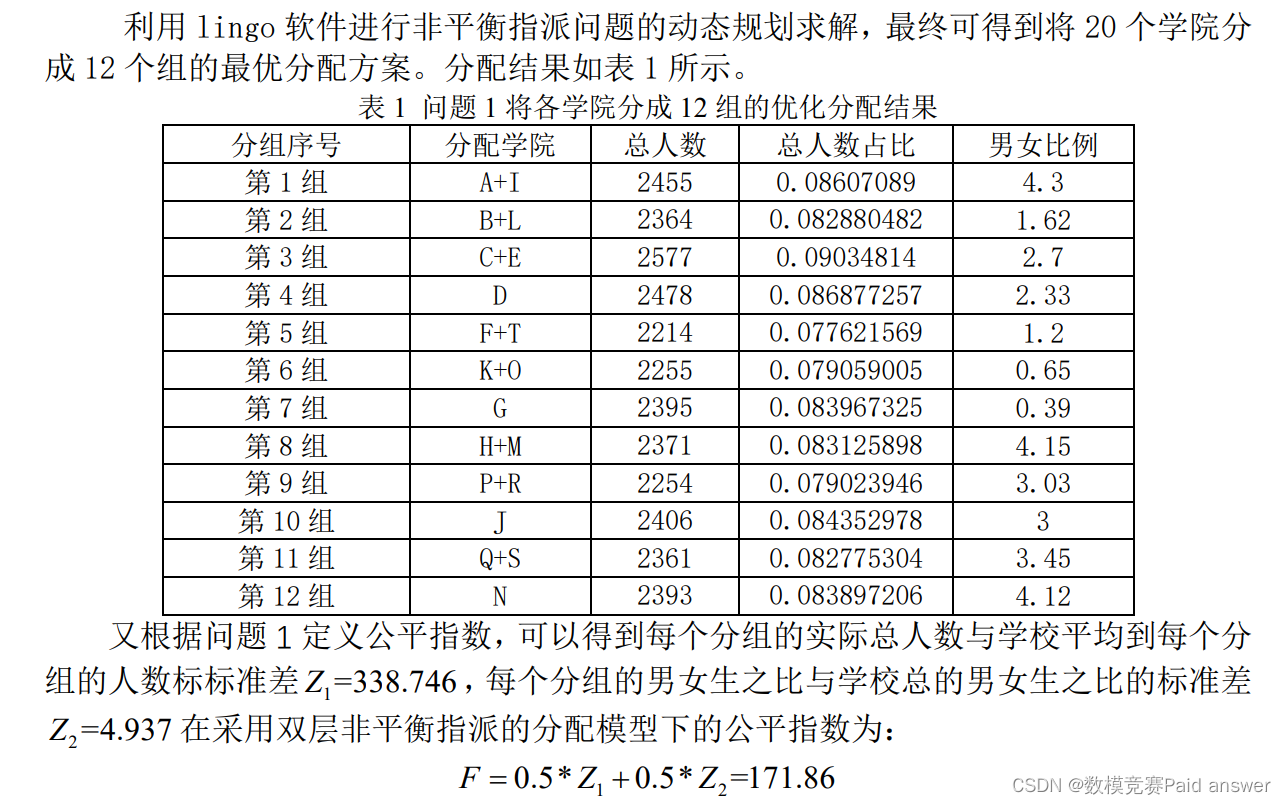
  若要对各个学院进行甲组和乙组分类进行比赛，根据题目给定的数据，可以按照男女性别将每个分为甲组和乙组，也可以考虑按专业将每个学院进行分组，将每个学院的总人数按照不同专业分为甲乙两组。结合问题 1，为了使得各组人员总数和男女性别比较为均衡的要求，我们选择按专业将每个学院进行分组。再利用问题1建立的非平衡指派的优化分配模型对按专业分组的每个学院进行分组求解，并讨论该分组方式的公平指数，最终确定最优的甲乙组分配方案。

按专业分组模型的建立

模型的求解

  结果

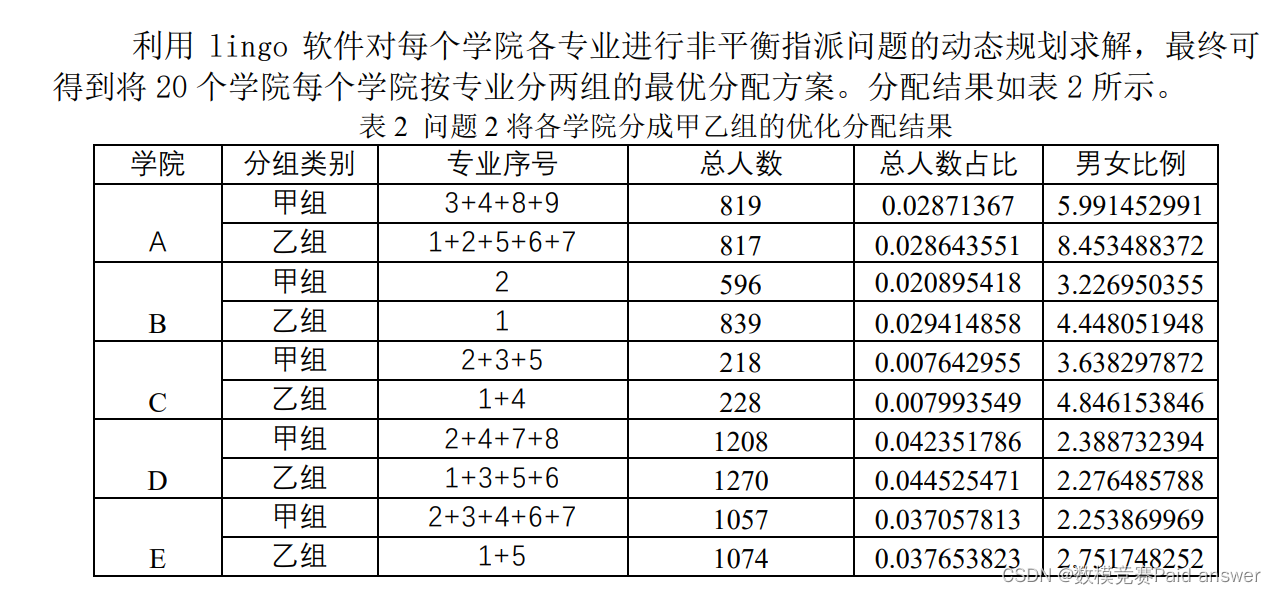
建立基于资源分配的特长生分配模型

  资源分配是一种或几种资源（包括资金）分配给若干用户，或投资于几家企业，以获得最大的效益的问题。资源分配问题可以是多阶段决策过程，也可以是静态规划问题，都能构造动态规划模型求解。以附件 1 中给出的各学院人数加上按比例分配后的特长生人数与学校平均到每个学院的人数的标准差最小作为目标函数，求解出特长生最优分配方案，然后再利用问题 1 定义的公平指数定义讨论其公平指数。

建立基于公平席位分配的加权积分模型

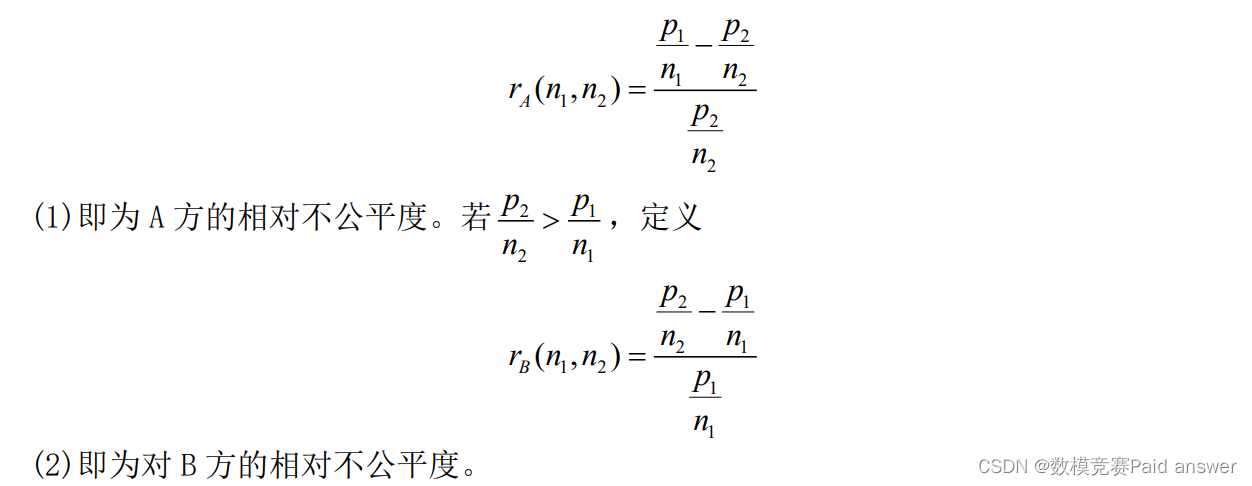
论文缩略图：

程序代码：

#include
int main(){
//int a[]={},b[]={};
//int z=6,x=6,c=6,v=6,b=6,n=6,m=6,l=6;
int z,x,c,v,b;
int man=714,woman=101,l=0;
double a[9]={135,145,41,170,112,192,143,250,240},
s[9]={5,10,7,21,33,34,4,42,47},
h,j,k,p=0.127,q=0.625;
for(z=8;z>=0;z--)
for(x=8;x>=0;x--)
for(c=8;c>=0;c--)
for(v=8;v>=0;v--)
{
if(z!=x)
if(z!=c)
if(z!=v)
if(x!=c)
if(x!=v)
if(c!=v)
{h=p*(man-(a[z]+a[x]+a[c]+a[v]));
j=q*(woman-(s[z]+s[x]+s[c]+s[v]));
if(h<0)
{h=-h;}
if(j<0)
{j=-j;}
k=100-h-j;
l++;
printf("%d-----%lf-----%d%d%d%d%d-----%lf------%lf\n",l,k,z,x,c,v,b,h,j)
;
}}
return 0;
}
x1=[]#x1 为对应组数的最低前 n 位学院的男生人数，需自行输入进列表
y1=[]#y1 为对应组数的最低前 n 位学院的女生人数，需自行输入进列表
x2=[]#x2 为对应组数的最低次 n 位学院的男生人数，需自行输入进列表
y2=[]#y2 为对应组数的最低次 n 位学院的女生人数，需自行输入进列表
renshu1=[]#此为对应组数的最低前 n 位学院的总人数
renshu2=[]#此为对应组数的最低次 n 位学院的总人数
nansheng=[]#此为对应组数的男生总人数
nvsheng=[]#此为对应组数的女生总人数
zongrenshu=[]
bili=[]
for i in range(len(x1)):
a=x1[i]+y1[i]
renshu1.append(a)
b=x2[i]+y2[i]
renshu2.append(b)
for j in renshu1:
for m in renshu2:
c=j+m
zongrenshu.append(c)
n=1
for k in range(0,len(zongrenshu),n):
zongrenshus=zongrenshu[k:k+n]
print(zongrenshus)
for i in range(len(x1)):
d=x1[i]+x2[i]
nansheng.append(d)
e=y1[i]+y2[i]
nvsheng.append(e)
for j in nansheng:
for m in nvsheng:
f=j/m
bili.append(f)
for k in range(0,len(bili),n):
bilis=bili[k:k+n]
print(bilis)
52,104,54,73,66,43,46,22,68,83,51
192,201,151,148,121,177,163,76,155,188,145
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

#include
int main(){
//int a[]={},b[]={};
//int z=6,x=6,c=6,v=6,b=6,n=6,m=6,l=6;
int z,x,c,v,b;
//double q[8]={7.35 ,7.21 ,8.04 ,7.97 ,8.28 ,8.22 ,7.63 ,7.09 },
//w[8]={6.47 ,7.15 ,7.14 ,7.25 ,7.46 ,7.34 ,7.89 ,7.99 },
//e[8]={7.09 ,7.82 ,7.08 ,7.58 ,7.41 ,7.42 ,7.89 ,7.71 },
//r[8]={7.25 ,7.24 ,7.96 ,8.02 ,8.30 ,8.14 ,7.70 ,7.15 },
//t[8]={7.47 ,7.55 ,7.87 ,8.18 ,8.19 ,8.23 ,7.68 ,7.14 },
//y[8]={7.23 ,7.66 ,7.71 ,7.96 ,8.04 ,8.02 ,7.87 ,7.33 },
//u[8]={7.66 ,7.50 ,7.97 ,8.13 ,8.16 ,8.28 ,7.54 ,6.99 },
//i[8]={7.26 ,6.74 ,8.12 ,7.62 ,8.04 ,7.92 ,7.51 ,6.82 },
//h;
int man=331,woman=858,l=0;
double a[11]={52,104,54,73,66,43,46,22,68,83,51},
s[11]={192,201,151,148,121,177,163,76,155,188,145},
h,j,k;
//printf("%lf",y[0]);
//for(m=10;m>=0;m--)
//for(l=7;l>=0;l--)
for(z=10;z>=0;z--)
for(x=10;x>=0;x--)
for(c=10;c>=0;c--)
for(v=10;v>=0;v--)
for(b=10;b>=0;b--)
//for(n=7;n>=0;n--)
{
if(z!=x)
if(z!=c)
if(z!=v)
if(z!=b)
//if(z!=n)
if(x!=c)
if(x!=v)
if(x!=b)
//if(x!=n)
if(c!=v)
if(c!=b)
//if(c!=n)
if(v!=b)
//if(v!=n)
//if(b!=n)
//if(l!=z)
//if(l!=x)
//if(l!=c)
//if(l!=v)
//if(l!=b)
//if(l!=n)h
//if(m!=z)
//if(m!=x)
//if(m!=c)
//if(m!=v)
//if(m!=b)
//if(m!=n)
//if(m!=l)
//
{
h=0.417*(man-(a[z]+a[x]+a[c]+a[v]+a[b]));
j=0.227*(woman-(s[z]+s[x]+s[c]+s[v]+s[b]));
//printf("%lf--%lf\n",h,j);
if(h<0){
h=-h;
}
if(j<0){
j=-j;
}
k=100-h-j;
//if(z==10) z=A;
//if(z==11) z=B;
//if(x==10) x=A;
//if(x==11) x=B;
//if(c==10) c=A;
//if(c==11) c=B;
//if(v==10) v=A;
//if(v==11) v=B;
//if(b==10) b=A;
//if(b==11) b=B;
l++;
printf("%d-----%lf-----%d%d%d%d%d-----%lf------%lf\n",l,k,z,x,c,v,b,h,j);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82