顺序表和链表

1.线性表

线性表是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构

线性表在逻辑上是线性结构，连续的一条线。
物理结构上并不一定是连续的。
线性表在物理结构上存储时，一般以数组和链式结构的形式存储

常见线性表：顺序表，链表

顺序表

无头链表

2.顺序表

2.1 概念和结构

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构。
一般情况下采用数组存储元素，便于完成数据的增删查改。

顺序表分为两种：静态顺序表，动态顺序表

1.静态顺序表：使用规定长度的数组存储元素

数组长度不能进行改变

2.动态顺序表：使用动态开辟的数组存储元素

数组空间不够，可以进行扩容
默认扩容2倍，扩容一次扩多，浪费；扩少，频繁扩容，影响效率

2.2 接口实现

接口就是规定要程序做什么，但不在其中实现

动态顺序表的实现

定义数据类型和结构体

typedef int LSdatatype;
typedef struct List
{
	LSdatatype* a;
	int count;//顺序表中数据个数
	int capacity;//顺序表容量
}LS;
1
2
3
4
5
6
7

初始化顺序表

必须通过指针才能改变结构体的内容，所有接口都需要传址，而不是传值

//初始化顺序表
void LSinit(LS* ps);

void LSinit(LS* ps)
{
    //需要进行判断，如果是空指针直接结束程序
	assert(ps);
	
	ps->a = NULL;
	ps->count = 0;
	ps->capacity = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12

尾插

在进行尾插时，需要考虑内存是否充足，否则就会出现问题。由于在整个程序中，还有其他功能需要判断内存是否充足，所有便将其独立为函数。

void Checkcapacity(LS* ps)
{
	//检查容量
	if (ps->count == ps->capacity)
	{
		int newcapacity = ps->capacity;
		//如果容量为0，则赋值为4个int的容量；
		//若不为零，则扩容二倍
		newcapacity == 0 ? 4 : 2 * ps->capacity;
		//为了避免内存开辟失败而将指针置为空，便创建临时变量tmp
		LSdatatype* tmp = (LSdatatype*)realloc(ps->a, newcapacity * sizeof(int));
		
		if (tmp == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

对于realloc函数一般的理解是扩容，但这里就直接拿来开辟内存，是否由问题呢

答案是：没有问题

再一次地仔细地观察realloc函数的定义

如果返回值为空指针，则 realloc函数与 malloc函数类似

所有以后如果遇到类似的情况也不妨使用 realloc函数，更加的高效。

尾插

//尾插
void LSpushback(LS* ps, LSdatatype x);


void LSpushback(LS* ps, LSdatatype x)
{
	assert(ps);
	//判断容量
	Checkcapacity(ps);
	ps->a[ps->count] = x;
	ps->count++;
}
1
2
3
4
5
6
7
8
9
10
11
12

尾 插数据 1，2，3，4，监视如下

头插

//头插
void LSpushfront(LS* ps, LSdatatype x);


void LSpushfront(LS* ps, LSdatatype x)
{
	assert(ps);
	//检查容量
	Checkcapacity(ps);
	int end = ps->count - 1;

	//挪动数据，从后往前挪
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[0] = x;
	ps->count++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

头插数据 5，监视如下

尾删

//尾删 --最简单直接将指针ps->a向前移动
void LSpopback(LS* ps);
void LSpopback(LS* ps, LSdatatype x)
{
	assert(ps);

	//温柔的检查
	if (ps->count == 0)
	{
		return;
	}

	暴力的检查
	//assert(ps->count > 0);
	ps->count--;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

数组删除数据不需要将数据清空，直接向前移动下标即可

如果数据都已经被删完，还继续删除数据的话，便会使内存崩溃，所有需要进行检查，有两个检查方式：温柔和暴力。

将数组第一个数据进行删除，监视如下

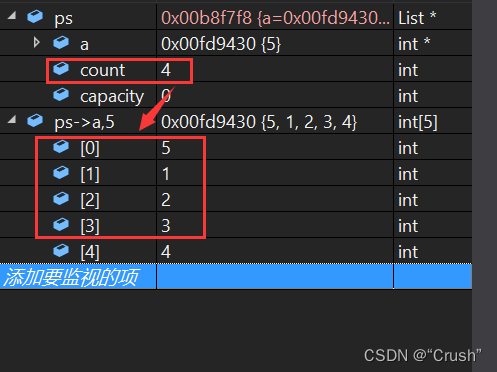
查找顺序表中的数据

//查找顺序表中的数据   找不到返回-1
int LSfind(LS* ps, LSdatatype* x);


int LSfind(LS* ps, LSdatatype* x)
{
	assert(ps);
	int i = 0;
	for (i = 0; i < ps->count; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}
	return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

在 pos位置 插入指定数据

//插入指定数据
void LSinsert(LS* ps, size_t pos, LSdatatype* x);

void LSinsert(LS* ps, size_t pos, LSdatatype* x)
{
	assert(ps);
	//相等时表示尾插
	assert(pos<=ps->count)
	
	Checkcapacity(ps);
	size_t end = ps->count;
	while (pos < end)
	{
		ps->a[end] = ps->a[end-1];
		end--;
	}
	ps->a[pos] = x;
	ps->count++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

由于pos和end的类型不同，循环条件的不同，可能会造成程序死循环
循环条件为 pos <= end时

这里虽然end 的 数值是负数，但在与pos 进行比较时，会转化为无符号整形，一个相当大的数值，程序便会进入死循环。

删除 pos位置 的数据

//删除数据
void LSerase(LS* ps, size_t pos);

void LSerase(LS* ps, size_t pos)
{
	assert(ps);
	assert(pos < ps->count - 1);
	size_t begin = pos;
	while (begin < ps->count - 1)
	{
		ps->a[begin] = ps->a[begin + 1];
		begin++;
	}
	ps->count--;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

修改 pos 位置 的数据

//修改数据
void LSmodify(LS* ps, size_t pos, LSdatatype x);

void LSmodify(LS* ps, size_t pos, LSdatatype x)
{
	assert(ps);
	assert(pos < ps->count);
	ps->a[pos] = x;
}
1
2
3
4
5
6
7
8
9

销毁顺序表

//销毁顺序表
//既然申请空间，在程序结束时便需要销毁空间

void LSdestory(LS* ps);

void LSdestory(LS* ps)
{
	assert(ps);
    free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->count = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

2.3 顺序表的问题及思考

1. 头部，中间的数据插入或删除，需要挪动数据，时间复杂度为O(N)
2. 增容需要开辟空间，有可能是原地增容，也有可能是异地增容。如果是异地增容需要拷贝数据，释放旧空间，消耗时间
3. 即使是2倍扩容，也会存在一定的空间浪费

解决以上问题，就需要引出下面的链表

3.链表

3.1 链表的概念和结构

概念：链表是一种物理结构上连续存储结构上非连续，非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的

逻辑结构

物理结构

1. 链式结构在逻辑上是连续的，在物理上却不是
2. 结点一般是从堆上申请的
3. 从堆上申请的空间可能会连续

3.2 链表的分类

实际中链表的分类的有很多，这里只介绍两类：单向不带头，双向带头

单向不带头：结构简单，一般不会单独用来存储数据。更多的是作为其他数据结构的子结构，例如哈希桶

双向带头：结构最复杂，一般用来单独存储数据。

3.3 链表的实现

单向不带头
定义类型和结构体

typedef int LSdatatype;
typedef struct Slist
{
	LSdatatype data;
	struct Slist* next;
}SL;
1
2
3
4
5
6

打印单链表

//打印单链表
void SLprint(SL* phead);

void SLprint(SL* phead)
{
	SL* tmp = phead;
	while (tmp != NULL)
	{
		printf("%d->", tmp->data);
		tmp = tmp->next;
	}
	printf("NULL\n");
}
1
2
3
4
5
6
7
8
9
10
11
12
13

销毁单链表

//销毁单链表
void SLdestory(SL* phead);

void SLdestory(SL** pphead)
{
	assert(pphead);
	SL* cur = *pphead;
	while (cur != NULL)
	{
		SL* next = cur->next;
		free(cur);
		cur = next;
	}
	*pphead = NULL;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

由于每个节点中都保存下一个节点的地址，不能直接释放*pphead，需要创建临时变量进行替换。

插入数据，便需要创建一个新的节点，由于新节点的创建不止出现一次，为了方便，将其独立为函数

SL* CreateSLnode(LSdatatype x)
{
	SL* newnode = (SL*)malloc(sizeof(SL));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return;
	}
	newnode->data = x;
	newnode->next = NULL;
	return newnode;
}
1
2
3
4
5
6
7
8
9
10
11
12

头插

//头插
void SLpushfront(SL** pphead, LSdatatype x);

void SLpushfront(SL** pphead, LSdatatype x)
{
	SL* newnode = CreateSLnode(x);
	newnode->next = *pphead;
	*pphead = newnode;
}
1
2
3
4
5
6
7
8
9

插入数据 1，2，3，4 监视如下

注意
改变数据，需要通过指针；改变指针，需要通过指针的指针。
由于上面是需要改变的指针，所有需要通过二级指针进行修改

在之后的学习中可以通过两种方式代替二级指针

1. 返回新的链表头
2. 设计为带哨兵位的链表

尾插

//尾插
void SLpushback(SL** pphead, LSdatatype x);

void SLpushback(SL** pphead, LSdatatype x)
{
	assert(pphead);
	SL* newnode = CreateSLnode(x);
	
	//1.plist 为空 改变结构体指针 
	if (*pphead == NULL)
	{
		*pphead = newnode;
	}
	
	//2.plist 不为空  改变结构体内容
	else
	{   
	    //找尾
		SL* tail = *pphead;
		while (tail->next != NULL)
		{
			tail = tail->next;
		}
		tail->next = newnode;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

尾插数据 5 ，监视如下

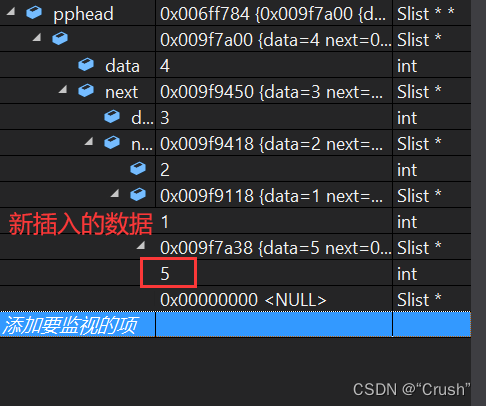
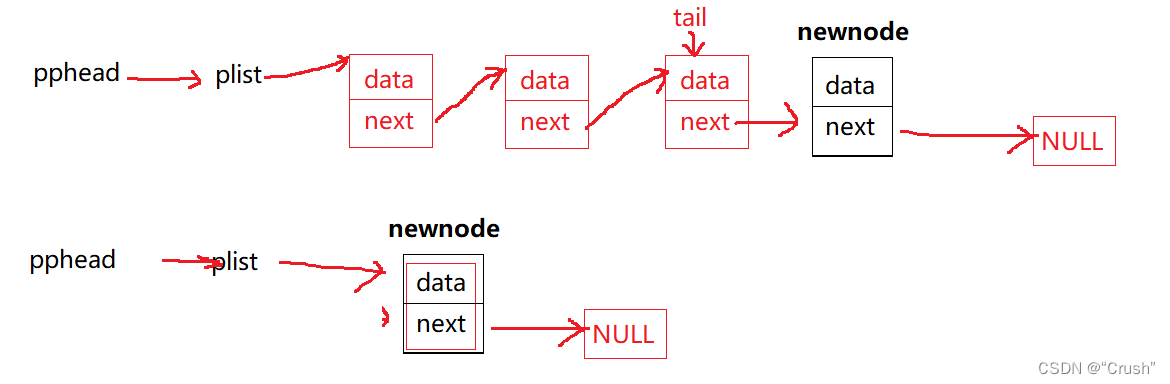
链表为空，插入第一个节点，改变SL*，通过结构体指针的指针pphead

链表不为空，插入节点，改变SL，通过结构体指针SL*tail

头删

//头删
void SLpopfront(SL** pphead);

void SLpopfront(SL** pphead)
{
	assert(pphead);
	SL* del = *pphead;

	//检查，避免数据删除完之后，继续删除数据，导致内存崩溃
	//1 温柔的检查
	while (*pphead == NULL)
	{
		return;
	}

	//暴力检查
	/*assert(*pphead != NULL);*/

	*pphead = (*pphead)->next;
	free(del);
	del = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

头删数据 4，监视如下

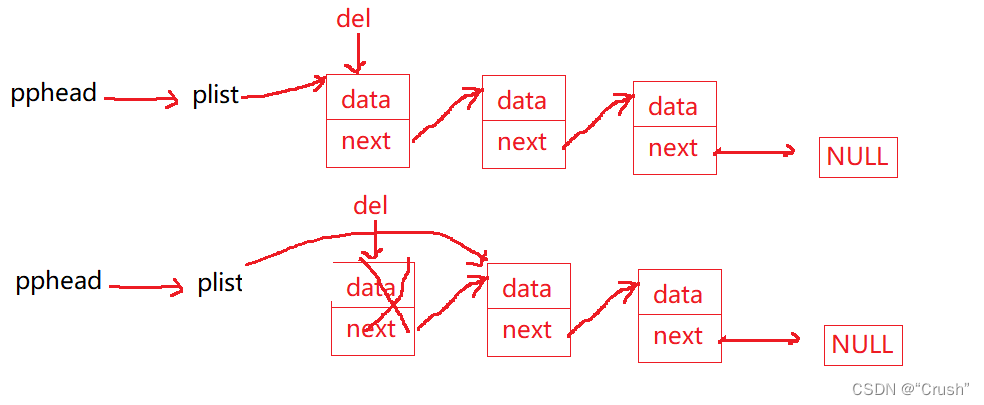
如果直接将第一个节点删去，就不能找到第二个节点，所以创建临时变量del保存第一个节点，之后再将其删去

尾删

//尾删
void SLpopback(SL** pphead);

void SLpopback(SL** pphead)
{
	assert(pphead);
	//1 温柔的检查
	while (*pphead == NULL)
	{
		return;
	}

	//暴力检查
	/*assert(*pphead != NULL);*/

	//1  一个节点
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	//2  多个节点
	else
	{
		方法1
		//SL* tail = *pphead;
		//while (tail->next->next != NULL)
		//{
		//	tail = tail->next;
		//}
		//free(tail->next);
		//tail->next = NULL;


		//方法2
		//找尾
		SL* tail = *pphead;
		SL* pre = NULL;
		while (tail->next != NULL)
		{
			pre = tail;
			tail = tail->next;
		}
		free(tail);
		tail = NULL;
		pre->next = NULL;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

尾删数据5，监视如下

查找节点

//查找节点
SL* SLfind(SL* phead, LSdatatype x);

SL* SLfind(SL* phead, LSdatatype x)
{
	assert(phead);
	SL* cur = phead;
	while (cur != NULL)
	{
		if (cur->data == x)
		{
			return cur;
		}

		cur = cur->next;
	}

	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

在pos之前插入新节点

//在pos之前插入新节点
void SLinsert(SL** pphead, SL* pos, LSdatatype x);

void SListInsert(SL** pphead, SL* pos, LSdatatype x)
{
	assert(pphead);
	assert(pos);


    //pos在第一个节点
	if (pos == *pphead)
	{
		SListPushFront(pphead, x);
	}
	else
	{
		SL* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;

			// 暴力检查，pos不在链表中，或者pos的值是错误的
			assert(prev);
		}

		SL* newnode = CreateSLnode(x);
		prev->next = newnode;
		newnode->next = pos;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

在数据 3，插入数据4，监视如下

在pos后面插入新节点

//在pos后面插入新节点
void SLinsertafter(SL* pos, LSdatatype x);

void SLinsertafter(SL* pos, LSdatatype x)
{
	assert(pos);
	SL* newnode = CreateSLnode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}
1
2
3
4
5
6
7
8
9
10

在数据1 后面插入数据 0，监视如下

删除pos位置

//删除pos位置
void SLerase(SL* pphead, SL* pos);

void SLerase(SL** pphead, SL* pos)
{
	assert(pphead);
	assert(pos);

	//pos是第一个节点
	if (*pphead == pos)
	{
		SLpopfront(pphead);
	}
	else
	{
		SL* tmp = *pphead;
		while (tmp->next != pos)
		{
			tmp = tmp->next;
		}

		tmp->next = pos->next;
		free(pos);
		//不需要将pos置空，改变pos不会改变链表
		//pos=NULL
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

将数据2所在位置进行删除，监视如下

删除pos后面的位置

//删除pos后面的位置
void SLeraseafter(SL* pos);

void SLeraseafter(SL* pos)
{
	assert(pos);
	if (pos->next == NULL)
	{
		return;
	}
	else
	{
		SL* next = pos->next;
		pos->next = next->next;
		free(next);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

将数据1所在位置后面的位置进行删除，监视如下

3.4 双向链表的实现

带头双向循环链表增删查改实现
1

定义类型和结构体

typedef int LTdatatype;

typedef struct LTlistnode
{
	struct LTlistnode* prev;
	struct LTlistnode* next;
	LTdatatype data;
}LTnode;
1
2
3
4
5
6
7
8

链表初始化

//链表初始化
LTnode* LTnodeinit();

LTnode* LTnodeinit()
{
	LTnode* guard = (LTnode*)malloc(sizeof(LTnode));
	if (guard == NULL)
	{
		perror("LTnodeinit fail");
		return;
	}
	guard->next = guard;
	guard->prev = guard;
	return guard;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

链表尾插
与单链表类似，插入数据，创建一个新的节点，由于新节点的创建不止出现一次，为了方便，将其独立为函数

LTnode* Buynewnode(LTdatatype x)
{
	LTnode* newnode = (LTnode*)malloc(sizeof(LTnode));
	if (newnode == NULL)
	{
		perror("Buynewnode fail");
		return;
	}
	newnode->prev = NULL;
	newnode->next = NULL;
	newnode->data = x;

	return newnode;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

尾插

//尾插
void LTnodepushback(LTnode* phead,LTdatatype x);

void LTnodepushback(LTnode* phead,LTdatatype x)
{
	assert(phead);

	LTnode* newnode = Buynewnode(x);
	LTnode* tail = phead->prev;
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

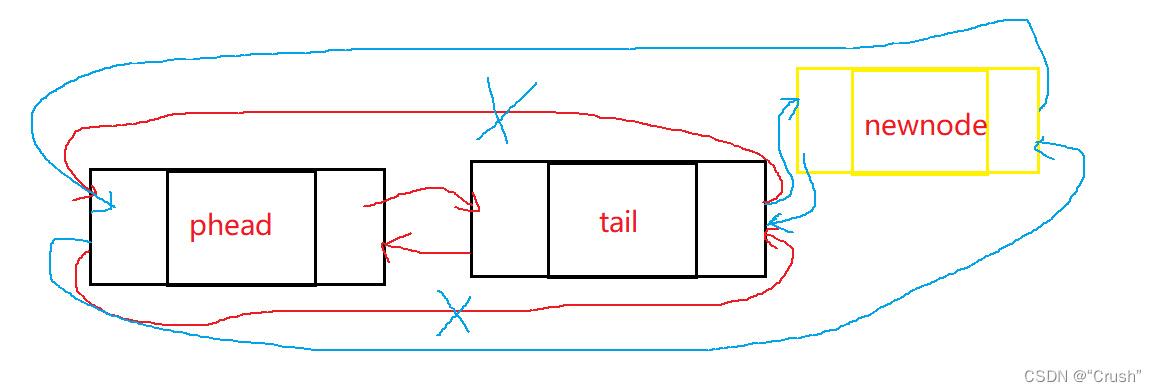
头插

//头插
void LTnodepushfront(LTnode* phead, LTdatatype x);

void LTnodepushfront(LTnode* phead, LTdatatype x)
{
	assert(phead);
	
	LTnode* newnode = Buynewnode(x);
	LTnode* next = phead->next;
	phead->next = newnode;
	newnode->prev = phead;
	newnode->next = next;
	next->prev = newnode;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

计算链表长度

这里使用size_t较为合适，如果使用char类型来记录链表长度，当链表长度超过128时，便会出错

//计算链表长度
size_t LTsize(LTnode* phead);

size_t LTsize(LTnode* phead)
{
	assert(phead);
	LTnode* cur = phead->next;
	size_t n = 0;
	while (cur != phead)
	{
		n++;
		cur = cur->next;
	}
	return n;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

判断链表是否为空

//判断链表是否为空
bool LTnodeempty(LTnode* phead);

bool LTnodeempty(LTnode* phead)
{
	assert(phead);
    //链表为空返回1，不为空返回0
	return phead->next == phead;
}

1
2
3
4
5
6
7
8
9
10

尾删

//尾删
void LTnodepopback(LTnode* phead);

void LTnodepopback(LTnode* phead)
{
	assert(phead);
	//链表不为空返回值为零，取反为真
	assert(!LTnodeempty(phead));
	LTnode* tail = phead->prev;
	LTnode* prev = tail->prev;

	phead->prev = prev;
	prev->next = phead;
	free(tail);
	tail=NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

头删

//头删
void LTnodepopfront(LTnode* phead);

void LTnodepopfront(LTnode* phead)
{
	assert(phead);
	//链表不为空返回值为零，取反为真
	assert(!LTnodeempty(phead));
	LTnode* prev = phead->next;
	LTnode* next = prev->next;
	phead->next = next;
	next->prev = phead;
	free(prev);
	prev=NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

链表查找

//链表查找
LTnode* LTnodefind(LTnode* phead,LTdatatype x);

LTnode* LTnodefind(LTnode* phead,LTdatatype x)
{
	assert(phead);
	LTnode* cur = phead->next;
	while (cur != phead)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

链表插入，在pos前插入节点

//在pos前插入节点
void LTnodeinsert(LTnode* pos, LTdatatype x);

void LTnodeinsert(LTnode* pos, LTdatatype x)
{
	assert(pos);
	
	LTnode* prev = pos->prev;
	LTnode* newnode = Buynewnode(x);
	prev->next = newnode;
	newnode->prev = prev;
	newnode->next = pos;
	pos->prev = newnode;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

删除pos位置的节点

//删除节点
void LTnodeerase(LTnode* pos);

void LTnodeerase(LTnode* pos)
{
	assert(pos);
	
	LTnode* prev = pos->prev;
	LTnode* next = pos->next;
	prev->next = next;
	next->prev = prev;

	free(pos);
	pos = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

打印链表

//打印链表
void LTnodeprint(LTnode* phead);

void LTnodeprint(LTnode* phead)
{
	assert(phead);
	printf("phead<=>");
	LTnode* cur = phead->next;

	while (cur != phead)
	{
		printf("%d<=>", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

销毁链表

//销毁链表
void LTnodedestory(LTnode* phead);

void LTnodedestory(LTnode* phead)
{
	assert(phead);
	LTnode* cur = phead->next;
	while (cur != NULL)
	{
		LTnode* next = cur->next;
		free(cur);
		cur = next;
	}
	free(phead);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

4. 顺序表和链表的区别和联系

顺序表优点：

1. 尾插尾删效率高
2. 随机访问（下标访问）

顺序表缺点：

1. 头部和中部插入或删除效率低 O(N)
2. 扩容时，存在性能消耗和空间浪费

链表优点：

1. 任意位置插入或删除效率高 O(1)
2. 根据需求申请释放

链表缺点：

1. 不支持随机访问