【基于机械臂触觉伺服的物体操控】论文研读《A control framework for tactile servoing》

我的毕设题目初定为《基于机械臂触觉伺服的物体操控研究》，这个系列主要用于记录做毕设的过程。因为目前我还在华工本校，这个题目是哈工深导师给我定的，所以我没办法做实验，应该只能在仿真环境中进行算法验证，又或许时间足够的话，我也会考虑搭建一个简易版的实验环境。无论如何，希望能够做出一个满意的毕设作品！

基础概念

触觉反馈：触觉传感器阵列提供的，在时间和空间维度都具有高分辨率和灵敏度的触觉数据信息
触觉伺服：基于触觉反馈的控制器
触觉伺服的应用任务：

1. 末端滑过物体表面
2. 跟随特殊的表面结构如“脊部”
3. 搜索独特的接触模块
4. 摸索出物体的形状

正是因为相关的任务太多太杂，所以需要有一个通用的框架来统一控制，进行任务实现。
该论文基于已有的未知环境的探索方案 — Raibert’s hybrid position and force control 进行进一步的研究。

论文内容

part2：STATE OF THE ART

《 Tactile sensors and the gripping challenge》：定义了基于触觉的探索和识别的五个阶段：approach（接近）, shape（形状）, texture（质地）, hardness（硬度） and thermal（热量）。
《Acquisition and interpretation of 3-D sensor data from touch》：通过操作物体去识别它，主要采用了多指机器人，先抓物体得到大致形态，再探索物体表面。突出点：跟踪线性特征，探索未知物体的表面，跟踪给点的接触位置。
《What can be inferred from a tactile arrayed sensor in autonomous in-hand manipulation?》：通过分析图像得到接触点坐标，物体姿态和接触力信息。

《 Using tactile data for real-time feedback》《Edge detection in tactile images》：通过霍夫变换拟合曲线，以此计算传感器坐标系下的受力方向。
《Efficient edge detection from tactile data》 In Proc. IROS, volume 3, 1995.：通过弹性理论获取接触的模型以及二维触觉传感器平面。
《Efficient edge detection from tactile data》 Trans. Robotics and Automation, 16(5), 2000.：提出了首个触觉伺服框架。

本论文就在上面的框架上做了两方面的改进：

1. 制定了一个灵活的控制器原型，可以很好地结合不同的触觉伺服任务。
2. 结合了传统的末端伺服和触觉伺服，可以提供便捷的接口来构成复杂的控制策略，以实现抓取，操作以及探测任务。

part3：FEATURE EXTRACTION FROM TACTILE IMAGES

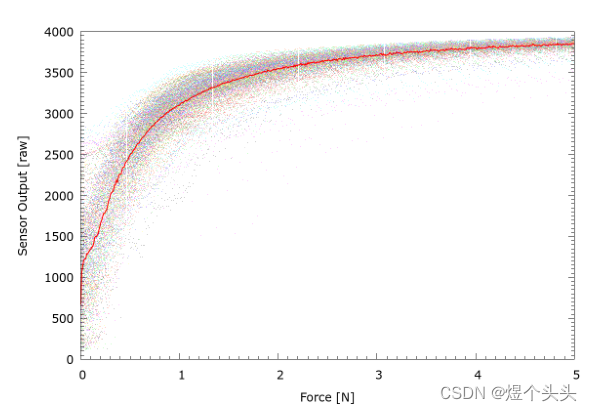
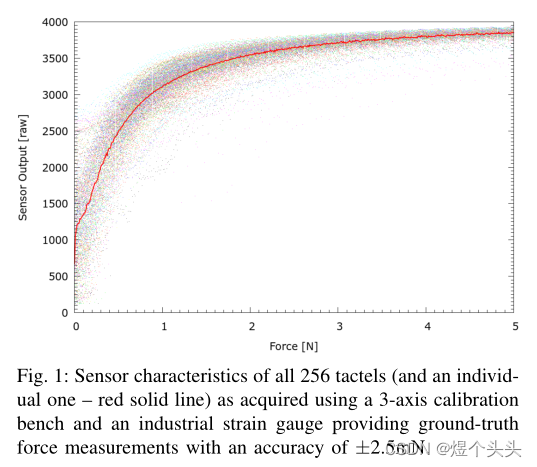
触觉传感器（tactile snesor）：16 x 16的方块阵列，每个方块的边长为5mm。每个方块的测量值可以转换为12bit的数值信号（0.1 - 10 kPa）。为了得到一个粗略的力标定，可以在其线性范围内对每个方块的特征测量函数进行反演。

伺服控制任务（需要通过特征提取方法来得到以下的控制变量）：

1. 操作末端的接触位置
2. 接触力大小
3. 物体边缘相对于传感器阵列的方向

处理方式：

1. 采用连接成分分析法，提取相关的区域，并且二值化阈值给的很小，以保证获取足够多的接触信息。
2. 计算接触力之和$f$以及压力中心c（COP）
   $$f=\sum _{ij\in R}{f}_{ij}，c=f^{-1}\sum _{ij\in R}{f}_{ij}{c}_{ij}$$
   
3. 计算压强值（对于很多易碎物体，一般控制的都是压强大小而非力大小）
   $$p=\frac{f}{|R|}$$
4. 提取物体边缘的线形接触区域的方向角

采用了两种方法：
基于霍夫变换的线性检测： 在灰度图像中拟合线段
图像矩分析： 提取接触区域中的主要成分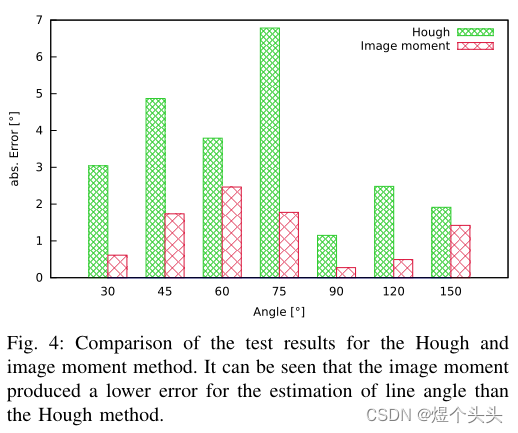

part4 TACTILE SERVOING FRAMEWORK

本论文提出的框架基于 《A hybrid architecture for adaptive robot control》中的control basis framework (CBF) 进一步拓展，实现了将控制任务的变量转换为机器人的关节角度

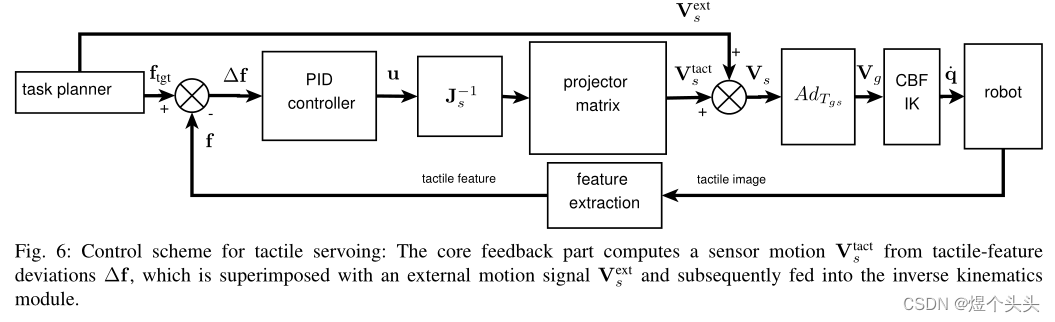
该框架的核心思想：通过定义逆雅可比矩阵$J_s^{-1}$，将触觉误差的特征向量映射至笛卡尔速度向量$V_s$，然后通过CBF控制器，控制机器人的关节运动，使传感器运动到计算所得位姿。
控制目标：在接触点运动的同时，保持目标输出力。

V s tact  = P ⋅ J s − 1 ⋅ ( K P ⋅ Δ f ( t ) + K I ⋅ ∫ Δ f ( t ) d t + K D ⋅ ( Δ f ( t ) − Δ f ( t − 1 ) ) )

Vstact ​=P⋅Js−1​⋅(​KP​⋅Δf(t)+KI​⋅∫Δf(t)dt+KD​⋅(Δf(t)−Δf(t−1)))​
V s t a c t = J s − 1 ⋅ Δ f = ( 1 1 1 0 1 1 0 1 ) ⋅ ( Δ x s Δ y s Δ f Δ α ) \mathbf{V}_s^{\mathrm{tact}}=J_s^{-1} \cdot \Delta \mathbf{f}=\left(

11101101" role="presentation">10111011$$\begin{array}{cccc}1& & & \\ & 1& & \\ & & 1& \\ 0& 1& & \\ 1& 0& & \\ & & & 1\end{array}$$

\right) \cdot\left(

ΔxsΔysΔfΔα" role="presentation" style="position: relative;">ΔxsΔysΔfΔα$$\begin{array}{c}\mathrm{\Delta }{x}_s\\ \mathrm{\Delta }{y}_s\\ \mathrm{\Delta }f\\ \mathrm{\Delta }\alpha \end{array}$$

\right) Vstact​=Js−1​⋅Δf=⎝ ⎛​101​110​1​1​⎠ ⎞​⋅⎝ ⎛​Δxs​Δys​ΔfΔα​⎠ ⎞​
P：0-1向量，用于筛选哪些控制成分需要考虑，如diag(1,1,0,0,0,0)，就只考虑x,y平面的线性运动。
${\mathbf{V}}_s^{\text{tact }}=[{\mathbf{v}}_s,{\omega }_s]$：传感器坐标系下的运动表达。
$J_s^{-1}$：将微分量映射为线性和旋转运动表达。

$\Delta x_s,\Delta y_s=>v_x,v_y$
$\Delta f=>v_z$
$\Delta y_s,\Delta x_s=>{\omega }_x,{\omega }_y$
$\Delta \alpha =>{\omega }_z$

A d T g s = ( R g s p ^ g s R g s 0 R g s ) A d_{T_{g s}}=\left(

\right) AdTgs​​=(Rgs​0​p^​gs​Rgs​Rgs​​)
$A{d}_{T_{gs}}$：坐标系变换矩阵，将传感器坐标系转换到世界坐标系。